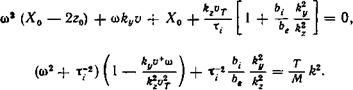О НЕУСТОЙЧИВОСТИ ГАЗОВОГО РАЗРЯДА В МАГНИТНОМ ПОЛЕ БЕЗ ПРОДОЛЬНОГО ТОКА
(Представлено академиком М. А. Леонтовичем 26 III 1963)
Как известно (1,[3]), тлеющий разряд при наличии постоянного тока вдоль внешнего магнитного поля неустойчив относительно извивания. Однако в ряде экспериментов (3~6) была обнаружена усиленная диффузия плазмы в бестоковом разряде с магнитным полем.
Ограничимся рассмотрением экспериментов, в которых диффузия плазмы была бестоковой. В опытах Желе (5) газ ионизовался высокочастотным полем. В этой работе было обнаружено критическое магнитное поле Яс, при котором появлялись интенсивные шумы и увеличивалась диффузия поперек магнитного поля. Критическое ноле убывало обратно пропорционально диаметру трубки и медленно росло с давлением нейтрального газа. Увеличенная диффузия при достаточно больших значениях Н наблюдалась также Голантом (ч). В этих опытах температура электронов была ниже, чем в (5), так как измерения производились через некоторое время после выключения высокочастотного поля.
Покажем, что наблюдавшиеся аномалии в поведении плазмы могли быть вызваны появлением дрейфово-диссипативной неустойчивости, на существование которой было указано в (7). Движение электронов будем рассматривать при помощи кинетического уравнения в дрейфовом приближении
£- * I - т < Iн*г, {- £ $ ат; = * (Л. 0)
Где столкновения с атомами нейтрального газа учтем посредством штосс
Члена (Л = — т;1 (/' — /„) т;1 (/ — /„) йиг. Здесь [ (х, vг) —
Функция распределения электронов, Д, = (т!2лТ)' 'п0 (х)е~тх)г'2Т, ф —потенциал электрического поля, хс — время между соударениями электронов с нейтралами, £>.. = еН/тс—циклотронная частота. Ось OZ направлена по магнитному полю, ОХ — по начальному градиенту плотности. Мы рассматриваем колебания с фазовой скоростью большей тепловой ионной, поэтому для ионов применимо гидродинамическое приближение, причем давление ионов можно не учитывать. Такое ограничение естественно, поскольку обычно в слабоионизованной плазме Те > Г,-. Таким образом, уравнение движения для ионов запишем в виде
Учет инерции ионов оказывается весьма существенным.
В экспериментах (5,6) разряд исследовался в диэлектрических—стеклянных трубках, поэтому ток на стенку должен отсутствовать. Как известно (см., например, (V)), при этом возникает электрическое поле
^ [ 1 - (От)х - (Йт),]"1 гг' ~ . Исследуя устойчивость, ограничимся
Квазиклассическим приближением, выбирая возмущения стационарных величин в виде причем будем считать ку > кх > х -= па' йп^йх.
В этом приближении детализация зависимости п0 и <р0 от х несущественна, а также оправдан переход к плоской геометрии.
Из уравнения (1), линеаризованного по малым возмущениям /х и ф1,
ДЛЯ возмущения ПЛОТНОСТИ электронов пи — ^ нетрудно найти
& = [-Н1 + у) + 1тг у]11 + (1 - у, м - (3>
Здесь
О
В гидродинамическом приближении, т. е. при VТ/т т, > к\ со < т“1, когда г > 1, У — (1 + 1/2г2), для пи получаем:
5* = ьл + 1Ы + оЛ{1 (4)
>
Здесь = Тхе/т, Ье = ете/гп — коэффициенты диффузии и подвижности электронов. Используя (2) и уравнение непрерывности, легко найти возмущение плотности ионов:
|
(5) |
![]() Лоф! - [— О? - г 7^ (— «•> - Г V)] 1 + (— - Г!)“)
Лоф! - [— О? - г 7^ (— «•> - Г V)] 1 + (— - Г!)“)
Исследование устойчивости будем производить следующим стандартным способом. Приравнивая из условия квазинейтральности возмущения плотности электронов и ионов, получаем дисперсионное уравнение для частоты. При нахождении границы области неустойчивости считаем 1т ю = 0. Приравнивая нулю по отдельности действительную и мнимую части дисперсионного уравнения, получаем условия для частоты и параметров плазмы, при
Которых наступает неустойчивость.
Длинноволновые ионно-звуковые колебания с ГТ/т ге > к]1 и частотой т^1 > © > й/ описываются системой уравнений гидродинамического приближения:
= _ь‘к'г +
(6)
= 4гк2 [со2 -}- /ютт1]1. л0ф1 М 1 ^
Ее исследование показывает, что при 5 '/Т/М хт, > (Йт), начинают
Раскачиваться колебания с о> ^ — ку УТ/М, ку^к (Йт)7 к] ^ /$Ь,-!Ье.
При (Йт), > 1, наряду с ионно-звуковыми, могут раскачиваться дрейфовые колебания, фазовая скорость которых порядка дрейфовой Т х
= - гг тт-. а частота со < Q^. Они описываются системой М 12,-
Из (7) находим, что при увеличении £, т. е. при уменьшении давления нейтрального газа, первыми раскачиваются колебания с ку ^ х (Йт),, к ^ кі фі! Ье) (Йт)72, при этом ^ 1, © ^ £уі/+. Верхняя по | граница определяется условием 5 < (Йт)/ феІЬі)1'.
При рассмотрении коротковолновых колебаний с кг > т*1 (Т/М)~' ' гидродинамическое приближение неприменимо.
Если т-1 > со > й/, то из (3), (5) получаем
![]()
![]() {т [1 + * *^7~2г»)] +
{т [1 + * *^7~2г»)] +
|
Е Ь* Лофі М 0)2 1 |
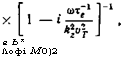 (3)
(3)
Здесь 20 а» Яе г ^ 1, Х0 = — 1У (г0) г'1 И + У (го)]”1.
На границе области устойчивости, когда 1ш © =0, из дисперсионного уравнения получаем:
Из (9) видно, что неустойчивость возможна лишь при |й)|^/гуо+. причем легче всего раскачиваются колебания с при наиболь
Шем возможном ку. Рассматриваемая неустойчивость относится к разряду дрейфовых (2,7), так как для ее существования необходимо, чтобы электроны могли выноситься наружу, дрейфуя в скрещенных полях —постоянном магнитном и электрическом поле волны. Поэтому необходимо, чтобы длина волны была больше гле = »гФ1. чем и определяется ку
Шах ^ Тле •
Из (9) получаем границу области неустойчивости по 5, лежащую несколько «ниже найденной в гидродинамическом приближении, а именно, при
До сих пор рассматривались неустойчивости диссипативного характера, для существования которых необходим сдвиг фаз между возмущениями плотности и потенциала, создаваемый необратимым процессом диффузии электронов. Однако при о > Т“1 к аналогичной раскачке могут привести эффекты взаимодействия с волной резонансных электронов, для которых уг = <а! кг. Для колебаний с г < 1, о > т;1, й,- имеем из (3), (5):
|
|
|
Лофі Т |
(10)
Е
Лофі М со2
Легко Видеть, что раскачиваются ионно-звуковые колебания с ю = — ку У Т/М, ку > (Г/М)''7* т;1, кг > ку (т/М)4', причем условие неустойчивости | > (Йт)4- совпадает с найденным гидродинамически.
Используя те же соображения, что и при нахождении кутах в (9), получаем, что неустойчивость возможна, если х < г£. Это определяет при-
Ближенно верхнюю границу рассматриваемой неустойчивости
I < (М/т)'' (Йт)|. Начальное электрическое поле обычно приводит к стабилизации (V). Нетрудно показать, что когда скорость дрейфа электронов в этом папе voy = — [1 + (Йт), (Qt)J-1 сравнивается по порядку
Т 1е
„ , Т х
|
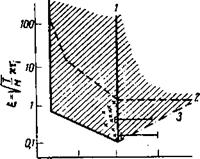
Рис. 1 |
![]() Величины со скоростью ларморовского дрейфа t/+ = —ц“» развитие неустойчивости прекращается. Поэтому неустойчивость возможна лишь при
Величины со скоростью ларморовского дрейфа t/+ = —ц“» развитие неустойчивости прекращается. Поэтому неустойчивость возможна лишь при
(От,) ^ (W - « 0,1.
Полная область неустойчивости изображена на рис. 1 (заштриховано^. Она состоит из трех перекрывающихся областей: 1 —дрейфовая область с
Со < Qi (эта область упоминалась в обзорной статье Б. Б. Кадомцева (8)).
|
0J ' (дr, 10 V^ |
![]() При очень больших значениях Я, когда Qi < tj[4], дрейфовая неустойчивость переходит в бесстолкновительную (9). 2 — ионно-звуковая область с а>>Ф, в которой при о < tj1 раскачка обусловлена диффузионным механизмом, а при w > ТГ1 резонансными электронами с vz = <»/£*. 3 — небольшая дополнительная область, где неустойчивы ионно-звуковые колебания, для которых существенна кинетика электронов с учетом столкновений. Максимальный инкремент в центральной части области неустойчивости порядка х~[5].
При очень больших значениях Я, когда Qi < tj[4], дрейфовая неустойчивость переходит в бесстолкновительную (9). 2 — ионно-звуковая область с а>>Ф, в которой при о < tj1 раскачка обусловлена диффузионным механизмом, а при w > ТГ1 резонансными электронами с vz = <»/£*. 3 — небольшая дополнительная область, где неустойчивы ионно-звуковые колебания, для которых существенна кинетика электронов с учетом столкновений. Максимальный инкремент в центральной части области неустойчивости порядка х~[5].
На рис. 1 крестиками указаны примерные значения параметров т] = (Qtji/g, 5 в опытах ([6]) при разряде в водороде. Отметим, что, как следует из результатов одного цикла измерений, значения Нс, приведенные в (5), соответствуют максимальной амплитуде колебаний. Если предположить, что неустойчивость, наблюдавшаяся Желе, вызвана раскачкой ионного звука, то зависимость Нс = const - d-1, зафиксированная им, получает естественное объяснение. Действительно, в уравнения (6), (10) входит только такая комбинация. Повышенная диффузия, наблюдавшаяся Голантом (в), вероятно, также связана с рассматриваемой неустойчивостью, поскольку данные эксперимента, отмеченные на рис. 1 отрезками, попадают в область неустойчивости.
Так как длина разрядных трубок в ([7], 6) намного превышала диаметр, то уход на торцы можно было не учитывать и выбор возмущений в виде плоских волн по Ог вполне оправдан. Непосредственное применение полученных формул к экспериментам ([8], [9]), хотя и дает обнадеживающие результаты, неправомерно, поскольку уход на торцы в этих опытах мог существенно влиять на развитие неустойчивости. Так, например, если электроны и ионы уходят на торцы с разной скоростью, этот эффект может играть роль диссипации, способствуя развитию неустойчивости.
Автор выражает глубокую благодарность Б. Б. Кадомцеву, под руководством которого была выполнена эта работа.
Поступило 6 III 1963