ФИЗИКА ПЛАЗМЫ

ДРЕЙФОВАЯ НЕУСТОЙЧИВОСТЬ НЕОДНОРОДНОЙ ПЛАЗМЫ В МАГНИТНОМ ПОЛЕ

1. Как известно, в неоднородной плазме, находящейся в магнитном поле, всегда имеются дрейфовые потоки электронов и ионов. По аналогии с обыч­ной пучковой неустойчивостью можно думать, что такие потоки должны приводить к раскачке волн, фазовая скорость которых поперек магнитного поля порядка дрейфовой. Такие волны, которые могут быть названы дрей­фовыми, действительно существуют в неоднородной плазме. Их исследова­ние было начато работой Ю. А. Церковникова (х), где на примере плазмы, находящейся в поле прямого тока, было показано, что при наличии гради­ента температуры может иметь место раскачка дрейфовых волн, распрост­раняющихся поперек магнитного поля. Гидродинамическое рассмотрение приводит нримерно к такому же условию устойчивости (2). В работе Л. И. Рудакова и Р. 3. Сагдеева (3) была рассмотрена косая дрейфовая волна, пе­реходящая в ионно-звуковую при уменьшении угла между волновым вектором и вектором магнитного поля. При почти поперечном распростра­нении такая волна обладает очень малым затуханием, а при наличии гради­ента температуры (3) или продольного тока она может стать нарастающей во времени.

В настоящей работе, в отличие от перечисленных выше, учитывается эф­фект конечного ларморовского радиуса ионов (см. (4)).

2. Рассмотрим неоднородную плазму, находящуюся в однородном маг­нитном поле Н, направленном вдоль оси г. Ограничиваясь одномерным слу­чаем, будем считать, что равновесные функции электронов fe и ионов ft - за­висят только от одной пространственной координаты х. Если функции f / мало изменяются на длине среднего ларморовского радиуса, то в системе коор­динат, где среднее электрическое поле отсутствует, имеем:

Ff = fo,(vi, v„x)+^d-!g, (1)

Где v2± = v - f - Qj = ejH/mjc, ef — заряд, mt — масса частицы сорта /.

Мы рассмотрим здесь волны продольного типа, распространяющиеся поперек градиента плотности. Для таких волн потенциал электрического поля можно выбрать в виде<р' =ф exp (— mt — ikzz -f ikyy), и тогда ре­шение кинетического уравнения для возмущения функции распределения f'i сорта / запишется в виде интеграла по траекториям (см., например, (4)):

Е ° df

F, = 'Ф ^ k ~d7(iY exP (~ Ш + ^ ikMi (0) dt, (2)

—CO

T

Где у/ (t) — ^ vyj (t) dt =-^cos (Qjt —“ф) —cos j), — азимутальный

О 1 1

Угол в пространстве скоростей. Для возмущений с длиной волны, много большей дебаевского радиуса, дисперсионное уравнение можно получить

Просто из условий квазинейтральности 2^/// =0. Мы предположим

Что распределение электронов и ионов по поперечным скоростям является максвелловским с температурами Ти Т±г соответственно. Так как функ­ция (1) не зависит от времени, то после дифференцирования по у ее можно вынести из-под интеграла по времени, и тогда дисперсионное уравнение преобразуется к виду

У ку?!±/ — куиу1(/) г

^т1- диг ' т^. дх Т^ '0/

= ‘ 2 ^ (т^т + 2 — пй/ + «V)'1 X

•5п'г' тд. 17 т; I

Где через Т7/ обозначена функция распределения от продольной скорости, Ра/ = /„ (6/); /п—функция Бесселя от мнимого аргумента; 6/ —

= ^Г_1_//т/й/; V — малая положительная величина, введенная для пра­вильного обхода полюсов.

3. Рассмотрим колебания изотропной (Т± = Т,|), изотермической (Те = Г/) плазмы с максвелловским распределением электронов и ионов по продольной скорости а2 и постоянной температурой [йТ/йх = 0). Предпо­лагая, что частота колебаний много меньше циклотронной частоты ионов, мы можем пренебречь в сумме по гг в (3) всеми членами, кроме нулевого. Ограничиваясь, кроме того, колебаниями с поперечной длиной волны, много большей среднего ларморовского радиуса электронов, положим Ье = 0. При этих предположениях уравнение (3) приводится к виду

(г а) РУ (г) — р (г — а) У (рг) = 2, (4)

Где г =£- у ; Ь = /г*р= = р =Уте! пц<^ 1, а = — |/"^

Х - г™— , Р ~е~ь10(Ь) /„—функция Бесселя от мнимого аргумента; У (г)-~ кга

Г

= 2е~г*ег~ & — I а — характерная длина, на которой заметно из-

0

Меняется средняя плотность плазмы п0: а'1 = (X 1п п0/с1х.

Исследование уравнения (4) показывает, что при а < 0, когда фазовая скорость волны направлена в сторону дрейфа ионов, волна является чисто затухающей, причем ее затухание экспоненциально мало при ар^> 1. Та­кие волны могут возбуждаться продольными пучками электронов или ионов. Что касается волн, распространяющихся в сторону дрейфа электронов (а > 0), то для их нарастания во времени оказывается достаточным лишь наличие градиента плотности.

Рассмотрим сначала область 1. При достаточно большом а, т. е. ма­лом г будет достаточно велико, и тогда приближенно У (г)^ 1/г. Если, с другой стороны, ра 1, то рг также будет значительно меньше единицы.

При этом У (рг) ^ — /}Лт, и из (4) получаем:

1т со _3 V"2лЬр 1 — 3 ^ 3

V0 “ V (2~Р)а V0 = 2“3 ’

Где и0 = 77ат, Й,- — дрейфовая скорость.

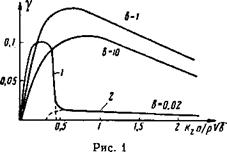
Как мы видим, инкремент нарастания малых возмущений 1т о> растет при уменьшении £*а. Это возрастание продолжается до тех пор, пока величи­на ра станет порядка единицы и уже нельзя пользоваться разложением для У (рг). Результаты численного расчета инкремента вблизи максимума для трех значений Ь (Ь = 0,02, Ь = 1, Ъ = 10) приведены на рис. 1. По оси абсйисс отложена безразмерная величина УЬ, по оси ординат — без­

Размерный инкремент у = т(аУЫкуи0.

Инкременту, обусловленный раскачкой резонансными электронами, т. е. возникающий за счет вычета, уменьшается пропорционально Ь2 при малых Ь. что видно, например, из (5). Однако при очень малых Ь (Ь 0,1) возникает неустойчивость гидродинамического характера на возмущениях с очень большой длиной волны вдоль 2 (ар ^>1). Для таких возмущений можно

1 1

Воспользоваться асимптотическим разложением У (рг) ^ » и тогда

Из (4) получим:

= 2 РгЬг (6)

Нетрудно получить условие появления комплексных корней у этого уравнения третьей степени. Условие имеет вид агр’Ь > 4 (1 --УЪ)~1х х(3 -}- У5)-2^0,09. На кривой 6 = 0,02 (рис. 1) этой неустойчивости соот­ветствует участок 1.

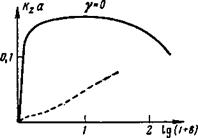
На рис. 2 представлена граница неустойчивости к^а = / (Ь) для р = 1.43. При малых Ь она определяется условием Ке г < а и приближенно &га = Ь, а при Ъ ^ 1 граничное значение определяется ионным затуханием и ока­зывается почти не зависящим от Ь. Пунктирнгя кривая на рис. 2 показы­вает, где инкремент у при фиксированных значениях Ь достигает максимума по

С помощью дисперсионного уравнения (3) можно произвести исследова­ние устойчивости и в более общем случае неизотермической неизотропнон, плазмы, но эта задача выходит за рамки настоящей статьи. Отметим лишь, что поскольку исследованная здесь раскачка волн обязана электронам, инкремент 1т о определяется в основном электронной температурой. В част­ности, неустойчивость имеет место и в предельном случае холодных ионов Т£ < Те. Отсюда следует, в частности, что наряду с эффектом конечности ларморовского радиуса к сдвигу фазы волны, способствующему неустойчи­вости, приводит также инерция ионов.

4. Итак, мы показали, что неоднородная изотермическая плазма в силь­ном магнитном поле является неустойчивой по отношению к раскачке воля дрейфового типа с поперечной длиной волны порядка среднего лармороа - ского радиуса ионов о,. Соответствующие возмущения сильно вытянуты вдоль силовых линий магнитного поля, и поэтому реально исследованная здесь неустойчивость может проявляться только в таких конфигурациях продольная длина которых L на порядок превышает поперечную а. " Так как поперечная длина волны нарастающих возмущений при не слиш­ком малых значениях a! L имеет порядок величины Р/, а вРемя развития ко­лебаний определяется величиной cl/pm, где v< = YTIrtii, то можно думать, что развивающиеся вследствие неустойчивости пульсации приведут к диффу­зии плазмы поперек магнитного поля с коэффициентом диффузии порядка pji't 'a. Этот коэффициент спадает как Н"2 с ростом магнитного поля, но па абсолютной величине он может значительно превосходить коэффициент диф­фузии за счет столкновений.

Авторы выражают благодарность Е. П. Велихову за обсуждение работы.

Поступило 14 IV 1962