Оценка экономической эффективности Инвестиций
Методы оценки экономической эффективности делятся на два больших класса: а) простые методы и б) методы дисконтирования.
Простые (статические) методы
Простые (статические) методы (или «экспресс-методы») позволяют достаточно быстро и на основании простых расчетов произвести оценку экономической эффективности. Это очень полезная информация, так как если проект «не проходит» по простым критериям, то можно быть почти уверенным в том, что он «не пройдет» и по более сложным.
В основе простых методов оценки экономической эффективности инвестиций лежит идея о том, что предприятие может оплачивать инвестиции из своей чистой прибыли и из амортизационных отчислений. Происхождение этих «составляющих» понятно: чистая прибыль остается в распоряжении предприятия, которое само решает, как с этой прибылью поступить; амортизационные отчисления по своей сути предназначены для инвестиций. В простых методах на основании таблицы движения денежных средств и отчета о прибылях и убытках оцениваются простая норма прибыли проекта, его простой срок окупаемости (ПСО) и точка безубыточности (ТБ).
Основные формулы расчета: -
ПНП=ЧП/ОИИ,
Где ПНП — простая норма прибыли проекта;
ЧП — чистая прибыль предприятия;
ОИИ — общие инвестиционные издержки.
Где ПСО — простой срок окупаемости проекта;
АО — амортизационные отчисления.
ТБ = (СС-УПЗ) / (ВР-УПЗ),
Где ТБ — точка безубыточности проекта;
СС — себестоимость продукции;
УПЗ — условно-переменные затраты;
ВР — выручка от реализации.
Общие инвестиционные издержки — это сумма денег, необходимая для проекта. Следует еще раз повторить, что к ее расчету надо отнестись очень внимательно (см. разд. «Оценка финансовой состоятельности проекта»).
Точка безубыточности проекта может рассчитываться только в товарных единицах, в рублях, в процентах к объему
Если точка безубыточности свыше 80% выпуска, это значит, что проект неустойчив; 80% средств им «проедается». Стоит подумать о снижении издержек и обувмичении объемов выпуска.
Методы дисконтирования
Методы дисконтирования основаны на сравнении денежных поступлений в различные моменты времени. Именно процедура дисконтирования позволяет максимально пол но учесть инфляцию, риски и альтернативную стоимость капитала на различных стадиях проекта.
Аксиомы расчета экономической эффективности инвестиционных проектов
Основой для расчета инвестиционных проектов являются две аксиомы, не нуждающиеся в доказательствах: они интуитивно понятны и не противоречат нашему практическому опыту.
Аксиома первая. У инвестора всегда есть выбор для вложения средств (принцип арбитражного ценообразования).
Аксиома вторая. Рубль сегодня стоит больше, чем рубль завтра (временная стоимость денег).
Но нелишне еще раз напомнить, что бизнес-планы — это очень важный аргумент в конкурентной борьбе за инвестиции.
Главными причинами того, что рубль сегодня стоит больше, чем рубль завтра, являются:
• инфляция;
• риски проекта;
• возможность альтернативного использования денег.
Инфляция — это уменьшение покупательной способности
Денег с течением времени или процесс роста средних цен. Инфляция означает, что за одни и те же рубли (доллары, франки, евро и др.) завтра можно будет купить товаров меньше, чем сегодня. Наиболее универсальный показатель измерения инфляции — это индекс потребительских цен, определяемый как «среднее подорожание средних товаров и услуг для типичного потребителя данной страны»,
Инфляция постоянно имеет место при денежном обращении. Нормальная инфляция — это как «нормальная температура». Высокая инфляция — это «высокая температура» в «больной» экономике. Она характеризует некий переходный период и может привести к «выздоровлению», в отличие от гиперинфляции, когда «очень высокая температура» может просто погубить «больного».
Инфляция способна резко изменить все основные параметры проектов, при этом важнейшей проблемой является ее «неравномерность». Дело в том, что цены на разные товары и услуги увеличиваются неодинаково. Так, например, в России за четыре месяца после дефолта 17 августа 1998 г. продукты питания подорожали в среднем в 1,95 раза, а услуги — всего на 18%.
Инфляцию, «которая была» и даже «которая есть», можно измерить хотя бы в принципе. Бизнес-план — это прогноз будущего. В нем нужно доказать, какая инфляция будет во время осуществления проекта. Гак появляются «сценарииинфляции» и «инфляционные ожидания», из которых исходят предприниматели и инвесторы. Само слово «ожидания» показывает, что здесь присутствует «человеческий фактор», а значит, велик разброс мнений.
Сложность прогноза инфляции в России усугубляется общей политической нестабильностью в стране, отсутствием признанных институтов, публикующих эти прогнозы, а также целым рядом других факторов.
Довольно часто в бизнес-плане предполагается, что цены реализации растут пропорционально инфляции, при этом увеличивается и объем продаж в натуральном выражения. Это предположение (как и любой другой сценарий) должно быть четко обосновано.
Единственный совет, который можно дать, — сначала просчитать проект в постоянных ценах, затем согласовать с инвестором сценарии инфляции и уже в процессе подготовки инвестиционного соглашения совместными усилиями подготовить расчет в реальных ценах.
Сравнение расчета в постоянных ценах, текущих ценах и в валюте
Постоянные цены соответствуют постоянной покупательной способности на весь период. При этом остальные величины должны быть выражены в аналогичных единицах. В жизни мы имеем дело с текущими ценами. Эти цены выражены в денежных единицах, соответствующих сегодняшней покупательной способности. В бизнес-плане для каждого периода его осуществления должны быть выбраны свои текущие цены с учетом инфляции. Постоянные цены — условность. Строго говоря, ни одна из валют не может оставаться неизменной и быть принятой в качестве
При расчете в текущих ценах денежные потоки (объемы выплат, поступлений, затрат) за определенный промежуток времени включают инфляционную компоненту (отслеживается выручка от реализации товара). В условиях инфляции идет рост реализации, и порой неясно, чем он обусловлен.
Может повышаться истинная стоимость товара, а может быть, это только инфляция. Нужно сравнение со средним индексом цен.
Ставки, которые фигурируют в условиях текущего момента, также имеют инфляционную составляющую (заимодавец ориентирован на сохранение текущей покупательной способности). Для выполнения расчета в постоянных ценах надо убрать инфляционную составляющую. Основные формулы для расчета номинальной и реальной банковских ставок приведены в разделе «Номинальная и реальная банковские ставки».
Возможность альтернативного использования денег. Деньги можно пустить в оборот и заработать на них. Дело вкуса — пускать их в торговый оборот, положить на депозит в банк или купить акции. Но пока деньги находятся на руках у инвестора, он имеет полную свободу выбора вариантов. Таким образом, люди, которые просят денег на свои проекты, всегда находятся в конкурентной борьбе за деньги инвесторов. Одним из наиболее мощных средств этой борьбы выступает бизнес-план.
Суммируя все сказанное, можно сделать вывод, что экономическая оценка инвестиционного проекта возможна
Расчет денежных потоков
|
В текущих иенах |
В постоянных |
В твердой валюте |
|
Все цены выражены в денежных единицах с покупательной способностью, изменяющейся в соответствии с темпами инфляции. |
Все цены выражены в денежныч единицах с Неизменной покупательной способностью. |
Все цены выражены в твердой валюте. |
|
Преимуществ я |
||
|
Приближение прогнозных величин денежных потоков К действительным, Возможность напрямую использовать в расчетах Стоимость капитала (процентные ставки, уровень дивидендных выплат, нормы прибыли). Относительная npOCTOTft моделирования структурной инфляции. |
Нулевой вариант П1П0ТСЗЫ о поведении внешних по отношению к проекту факторов неизменности). Простота подготовки и верификации исходных данных. Возможность сопоставления между собой численных величин денежных потоков для различных интервалов планирования. |
Те же, что и при «классическом» расчете в постоянных Удобство представления исходных данных и результатов расчетов при работе с иностранными партнерами. Возможность сопоставления между собой характеристик внутренних и зарубежных ин вестициснных проектов. |
|
Недостатки |
||
|
Сложность алгоритмов расчета номинальных величин денежных потоков. Трудность сопоставления между Численных величин денежных потоков для различных интервалов планирования. |
Необходимость Использования в расчетах Реальной (очищенной от инфляции) стоимости капитала. Сложность определения действительных (номинальных) сумм И дивидендных Выплат. Сложность учета влияния инфляции на потребность в оборотном капитале. Необходимость коррекции сумм Отчислений. |
Те же, что и при «классическом» расчете в постоянных Сложность учета Внутренней инфляции твердой валюты. |
|
Только с учетом всех факторов — инфляции, рисков и аль- |
Тернатив. Именно такую возможность дают методы дисконтирования.
Самое большое количество ошибок в расчетахдисконтиро - вания допускается из-за того, что нет ясного понимания экономической сути расчета.
Именно поэтому сначала следует проанализировать различные виды банковских ставок и простые модели финансовых расчетов с учетом временного фактора (депозиты, аннуитеты и перпетуитеты) и только потом — собственно дисконтирование денежных потоков и расчет характеристик экономической эффективности проекта.
Номинальная и реальная банковские ставки
Предположим, что на «семейном совете» решено купить компьютер за 1 ООО долл. США, а семья ежемесячно может откладывать по 2 300 руб. При курсе доллара на момент «совета», равном 22,5 руб., процесс накопления займет свыше 14 месяцев. Если в течение этого времени деньги будут работать, то можно сократить время накопления. Возникает идея положить деньги на депозит в банк и постепенно пополнять сумму. Но что лучше: хранить их в долларах, потом продать и получить рубли, чтобы оплатить покупку, или сразу копить в рублях? Ответ ясен: если увеличение рублевой суммы происходит быстрее, чем их обесценивание из-за инфляции, то лучше хранить деньги в рублях, и наоборот. Приведем формулы для расчетов.
Предположим, в рекламе банка указано, что «принимаются вклады населения под 10% в месяц». Здесь 10% — это «номинальная банковская ставка» М: получив от вкладчика 100 руб., через месяц банк выдаст ему 1 10 руб. Если за это время инфляция составила 15%, то реально деньги обесценились, поскольку покупательная способность у ПО руб. меньше, чем была у 100 руб. Формально денег больше, но купить на них можно меньше. Реальное увеличение покупательной способности денег характеризуют реальной банковской ставкой — Я. Эта ставка показывает, во сколько раз реально выросла покупательная способность денег за указанный период. При инфляции I, равной нулю (нет инфляции), номинальная и реальная банковские ставки совпадают. Тогда на полученные 110 руб. можно купить больше товаров. Во всех других случаях номинальная ставка состоит из двух частей — инфляционной и реальной.
Формула связи между реальной и номинальной ставками имеет вид:
N = (1 +I)-(1 + R)— 1 — зависимость номинальной ставки
От
К = (N-I)/(1 + I) — зависимость реальной ставки отноми - нальной.
Эти равенства носят название «формулы», или «правила», Фишера.
Срасчетом инфляции связано довольно много ошибок. Наиболее часто встречающаяся из них —расчет инфляции не по формуле Фишера, а по приближенной формуле К — N—I. Рассмотрим на примере, к чему это приводит при различных уровнях инфляции.
Допустим, инфляция равна 3% годовых, а N — 7%. По приближенной формуле
R—(N—I) =0,04.
По формуле Фишера
K=(N-l)/(l+l)=(0,07-0,03)/(l + 0,03) = 0,0398,
Что с достаточно высокой для расчетов точностью равно 0,04. Соответственно, при таких уровнях инфляции вполне возможно применение упрощенной формулы.
Уже при 50% инфляции и номинальной ставке 60% имеем: по упрощенной формуле
R =*(N—I) —0,1;
По формуле Фишера
К =(N—1)/(1+1)~ (0,6- 0,5)/(1 + 0,5) =0,067.
Ошибка достигает 45%, что может привести к качественно другим результатам.
Расчет значения банковского депозита
Предположим, что полнена давно обещанная премия и что можно какую-то ее часть (условно — 1000 руб.) отложить, так как она понадобится только в отпуске, через три месяца. Чтобы как-то уберечь деньги от инфляции, предполагается положить их в банк на депозит. Но отдавать деньги на длительный срок — опасно. Решено положить деньги на месяц в банк (это минимальный срок депозита в российских банках), а затем продлевать по мере необходимости. Пусть депозит приносит дохода за месяц. Тогда сумма денег (F,) в конце первого месяца будет равна:
F=1000x(l +0,1)
Сумма депозита на начало второго месяца будет равна той
Же
1 000х(1 +0,1). Еслисбанком ничего не произойдет и деньги останутся на депозите, то к концу второго месяца его сумма (F2) составит:
Fj=[l 000 х(1 +0,l)j х(1 +0,1)..
Если эта же сумма останется на начало третьего месяца, то в конце его можно получить сумму
F3 = {[] 000 х(1 +0,1)] х(1 +0,1)} х (1+0,1) F3 = 1000 х(1 +0,1)3.
Депозит — это инвестиции: деньги отдаются в банк с целью получения на них процентов. Обратите внимание: чем дольше лежат деньги на депозите, тем выше выифыш, но при этом выше и риск, что с банком что-то случится.
Общая формула расчета будущего значения депозита (формула сложных процентов) имеет вид:
|
193 |
FVn = РУСІ + К)",
134»
Где FV (Future Value) — будущая величина депозита;
IV (Present Value) — текущая, или современная, величина вложений;
К— прибыльность на инвестиции;
П — число стандартных периодов.
Расчет будущей стоимости депозита — это пример расчета, учитывающего временную стоимость денег. Верна и обратная формула:
PV =w„/<i + к г (1)
Будущая стоимость аннуитета
Аннуитет — это ежегодный взнос финансовых средств ради накопления определенной суммы в будущем. Два наиболее часто встречающихся примера аннуитета: амортизационные отчисления и дополнительная пенсия.
Из амортизационных отчислений формируется специальный фонд — это денежные средства, позволяющие приобрести новое оборудование взамен постепенно изнашивающегося старого. Экономический механизм накопления средств для замены признается налоговым законодательством всех стран, и величина амортизационных отчислений исключается из налогооблагаемой прибыли. Как мы уже говорили в разделе, посвященном финансовой характеристике проекта, амортизационные отчисления играют важную роль в инвестиционном процессе.
Задача 1. Предположим, что амортизационные отчисления удалось перечислять на специальный счет под 10% годовых. Перечисляться будет по 2 млн. руб. ежегодно в течение трех лет. Какой суммой будут обладать менеджеры в конце третьего года?
Решение задачи представлено в табл. 10.4.
|
Таблица 10.4
|
|
При расчетах учтено, что амортизация начисляется в конце года. Если об этом забыть, результат вычислений будет неверным. |
Ценность ренты
Очень часто альтернативой инвестиционному проекту выступают доходы в виде ренты. Классический пример ренты — бессрочный текущий счет, процентный доход по которому снимается сразу после его начисления. В этом случае основной вклад может «вечно» приносить деньги. Это пример псрпетуи - тета (от англ. perpetuity — «вечность»)- Годовой доход определяется по формуле
PVAn = PVx К
Где РУАп — годовой доход в п-м году;
РУ— основная сумма сбережений;
К — процентная ставка дохода, выплачиваемая
По счетам данного типа.
|
13' |
|
195 |
Пусть у инвестора есть счет в банке на 1000 руб. под 60% годовых. Это значит, что каждый год можно брать со счета 600 руб. прибыли. Отсюда простой вывод: если вложение денег на счет в банке под 60% годовых даст прибыль 600 руб., то нет
смысла выделять их на инвестиционный проект, который может иметь в конце каждого года более низкую доходность.
Задача 2. Фирма предлагает купить акции. Сегодняшняя цена за одну акцию — 25 руб. В проспекте эмиссии указано, что через 5 лет ее цена будет не менее 50 руб. Стоит ли покупать акции или лучше положить деньги на депозит под 10% годовых?
Решение. Самый простой способ решения задачи — подсчитать, какова будет сумма денег, если пять лет держать их на депозите.
Результат получим по формуле сложных процентов: FVn =PV(1 +К/=25 (1+0,1)5-25 1,610 = 40,25 руб.
Однако трудно понять, какую реальную покупательную способность будут иметь 40,25 руб. через пять лет и 50 руб. — через те же пять лет. Эта разница в покупательной способности может быть едва различима. Значительно нагляднее для инвестора сравнение сегодняшних (текущих) денежных сумм. Так, с помощью формулы (1) можно провести сравнение в обратном порядке и узнать, какую сумму нужно сегодня положить на депозит под 10% годовых, чтобы через пять лет получить те же 50 руб. Формула в этом случае имеет вид:
PVe =FV/1+K)= 50/(1 + 0,1 У = 50 0,6209 = 31,05 руб.
Результат очень просто интерпретировать. Для того чтобы через пять лет получить 50 руб., можно сегодня потратить на акции 25 руб. или положить на депозит 31 руб., т. е. примерно на 24% больше. Такой способ, когда все доходы и расходы проекта приводятся к текущему моменту, играет принципиально важную роль в процессе коммерческого анализа инвестиционного проекта. Как правило, акция — это более рискованное вложение, чем депозит, но и более прибыльное. После расчета уже есть реальные цифры доходности (по рискам их получить гораздо сложнее) и можно понять, чем вы рискуете и насколько оправдан этот риск. Следует сказать: если эти деньги далеко не последние, то нужно вкладывать ^ их в акции, а если предпоследние, то лучше вообще держать их дома.
Любой предприниматель, приходя к потенциальному инвестору, говорит по сути одно и то же: «Дайте мне сейчас 1000 руб. Смогу отдавать по 100 руб. в месяц в течение 10 месяцев». Но для инвестора сто рублей через месяц и те же сто рублей через два месяца — это разные риски, разные инфляции, разные возможности альтернативного использования денег, а значит, и разные суммы.
Чтобы сравнить деньги, которые предполагается получить через различные моменты времени, нужно провести расчет текущей (современной), или дисконтированной, стоимости.
Дисконтирование
Как мы уже отмечали, капитал имеет стоимость, связанную со временем его использования и характеризующуюся риском. Именно это — основа оценки экономической эффективности инвестиционных проектов. Одна и та же сумма 1000 руб. на разных участках инвестиционного проекта — это фактически несопоставимые величины. Денежные доходы, поступающие на предприятие в различные моменты времени, не должны суммироваться непосредственно. Можно суммировать лишь элементы приведенного потока. Если обозначить Fp Fy... Fn — прогнозируемый денежный поток но годам, то /-Й элемент дисконтированного денежного потока Р., рассчитывается по формуле
Р, = F/a+d/,
Где — коэффициент дисконтирования.
Экономический смысл коэффициента дисконтирования достаточно прост: он определяется тем соображением, что для инвестора сумма Я. в данный момент и F., через /лет представляет одинаковую ценность.
Назначение коэффициента дисконтирования состоит во вре-
Менной упорядоченности будущих денежных поступлений и в их приведении к текшему моменту времени. Используя формулу, можно приводить в сопоставимый вид оценку доходов, ожидаемых к поступлению в течение ряда лет.
В первом приближении коэффициент дисконтирования численно равен процентной ставке, устанавливаемой инвестором, т. е. тому относительному размеру дохода, который инвестор хочет или может получать на инвестируемый им капитал.
Чистая приведенная стоимость проекта (NPV)
Любой проект предполагает некоторые денежные вложения в расчете на последующие поступления. Задача дисконтирования — определить, сколько реально стоят будущие поступ» ления «в сегодняшних деньгах» с учетом рисков, инфляции, альтернатив. Первый пример такого типа был уже нами рассмотрен в задаче 2. Там проект состоял из одного вложения (покупка акции или депозитное соглашение) и одного поступления (выплата по акциям или сумма надепозите). Для сравнения их эффективности мы привели оба значения к сегодняшнему моменту. Это простой пример. Реальный проект может требовать вложений и приносить прибыль на каждом интервале планирования. Чтобы знать в реальности, сколькоденегтре - бует проект и сколько он может их принести, необходимо элементы денежного потока на каждом интервале проекта привести к текшему моменту. Если Ft — элементы притока денег от проекта, а — инвестиции на различных интервалах, то формула для чистой приведенной стоимости проекта будет иметь вид:
Яр " /
------- V—^—
Задача 3. Предлагается инвестиционный проект, предполагающий получение 2 млн. руб. в конце каждого из последу - ющихтрехлет. Чему равна его приведенная стоимость при ставке дисконтирования
Экономический смысл задачи можно пояснить на конкретной ситуации: предприниматель приходит в банк и просит выдать ему 6 млн. руб., обещая вернуть их в течение трех лет по 2 млн. руб. в год. Совершенно ясно, что банк откажет в такой «ссуде». Почему? Во-первых, дать надо сегодня, и притом все 6 млн. руб., потом ждать, атем временем инфляция будетделать свое дело, реально уменьшая стоимость возвращаемых денег; во-вторых, сегодняшние 6 млн. руб. при их грамотном использовании за три года могут дать весомую прибыль; в-третьих, предприниматель может разориться. Дать деньги, потом ждать три года их возврата и получить те же деньги — подобную сделку банку можно предложить только в шутку. А если говорить серьезно, то надо договариваться о процентах или дисконтах. Коли известен коэффициентдисконтирования, то договориться просто:' нужно предложить банку выдать сегодня сумму, равную чистой приведенной стоимости проекта за три года. Рассчитаем чистую приведенную стоимость, исходя из планируемых денежных потоков.
Решение.
Решение задачи представлено в табл. 10.5.
|
Таблица 10.5.
|
|
Итого NPV 4,972 |
|
|
Где РМТ, — будущий платеж в конце периода Т; d — необходимая (конкурентная) норма доходности по инвестициям;
Ft — число периодов, на протяжении которых в будущем поступят доходы от современных инвестиций.
Особый случай — инвестиции с неограниченным сроком жизни, но с постоянно возрастающими величинами годового дохода. Если такой рост происходит с темпом, равным & а Fs — ожидаемая величина денежных поступлений в конце первого периода, тогда текущая (современная) стоимость такой «вечной» инвестиции будет равна:
NPV= Ft/(k — 10 (модель Гордона) Условия применимости.
1. Отправной точкой отсчета служит платеж (денежные поступления) на конец первого периода их использования. Если же средства поступают к инвестору незамедлительно, то их величину следует прибавить к величине текущей стоимости, найденной по формуле Гордона.
2. Модель может использоваться только при постоянном возрастании денежных поступлений с одним и тем же темпом роста g.
|
Таблицу можно представить и в виде формулы |
|
NPV3 = 2/(1 +0,1)+ 2/(1 +0,1)3-2/(1 + 0Д)' |
|
Формула расчета NPVдля аннуитета в общем случае произвольных платежей и нормы дисконта имеет вид: |
3. Модель справедлива только в том случае, если темп роста g меньше, чем уровень доходности/:.
Характерными примерами инвестиций, рассчитываемых по модели Гордона, являются затраты, которые осуществляются
Для проникновения на новый региональный рынок или связанные с приобретением контрольного пакета акций.
Более общий случай расчета NPV рассмотрен в следующей задаче.
Задача 4. Завод предполагает купить оборудование. Его стоимость
Составляет 90 млн. руб. Кроме того, надо затратить в течение года еще не менее 35 млн. руб. на переоборудование помещений и установку механизмов. И еще потребуется один год для запуска производства одновременно с рекламной кампанией и кампанией «Паблик рилэйшнз», что обойдется в сумму не менее 20 млн. руб. Затем предполагается, что в течение 7 лет оборудование будетдавать прибыль по 40 млн. руб. в год. Через 10 лет это оборудование можно будет продать по цене 30 млн. руб. Определить NPV проекта при альтернативной норме доходности, равной 10% годовых.
Небольшой комментарии. Эта задача очень похожа на инвестиционный проект. Только здесь денежные поступления по годам как бы уже «рассчитаны за нас» — продиктованы условиями задачи, и в реальных проектах прибыль (40млн. руб. вгод)должна рассчитана.
Сделаем оценку на основании простых методов, без учета дисконтирования. Расходы по проекту составляют 145 млн. руб. (90+35+20). Доходы же равны 310 млн. руб., т. е. сумме денежных поступлений за 7лет(40-7= 280млн. руб.) и дохода от продажи оборудования (30 млн. руб.). Итого, затратив 145 млн. руб., получаем ЗІ0 млн. руб. Выигрыш составляет 165 млн. руб. (310* 145). Достаточно многообещающий проект!
Теперь учтем, что часть денег поступит через 8-10лет. По условию задачи у нас не очень хорошие возможности альтернативного использования денег (10% годовых — это совсем немного), но даже такая альтернатива значительно изменит результаты.
Решение.
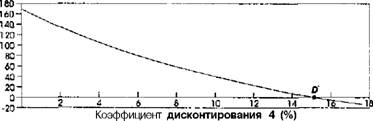
Решение задачи представлено в таблице (табл. Ю.6.). Если все расходы и доходы проекта привести к начальному моменту времени по ставке дисконтирования 10% годовых, прибыль составит всего 34 млн. руб. на 145 млн. руб. вложений. Проект остается прибыльным, хотя, кактолько появилась возможность сравнения доходностей, стало ясно, что из-за растянутого по времени поступления денег никаких «сверхдоходов» не наблюдается. Чем выше ставка дисконтирования, тем «плачевнее» будет результат вложений. Можно построить график зависимости чистой приведенной стоимости (N PV) от коэффициента дисконтирования (d).Для нашей задачи этот график показан на рис. 10.1. Он довольно типичен для «простых проектов», когда сначала делаются все вложения, а потом проект начинает работать и давать отдачу.
|
Таблица 10.6
|
|
NPV
Рис. 10.1 |
С математической точки зрения зависимость ОТУ от*/ представляет собой непрерывную кривую. Аналитическое выражение — сумма нескольких дробей с переменными знаменателями и постоянными числителями (напомним, числители задаются притоком денег от проекта, которые определяются самим проектом и не зависят от коэффициента дисконтирования!). Такая кривая пересекает ось абсцисс (ось X) в некоторой точке — она обозначена D*. Если коэффициент дисконтирования расположен левее этой точки, то проект — прибыльный (результаты всех расходов и доходов, приведенные к сегодняшнему дню, дают в сумме положительный эффект). Если же коэф - дисконтирования правее этой точки, то проект перестает быть прибыльным. Таким образом, коэффициент дисконтирования, точке имеет гранич
Ный характер и показывает эффективность самого проекта, так как точка может быть получена, исходя из потоков денежных средств, генерируемых проектом. Точка парамет
Ром, характеризующим «экономический кпд» проекта. Она называется «внутренней нормой доходности проекта» и обозначается
В экономической литературе можно встретить и другие названия для 1КК. Поэтому авторы предпочитают ставить рядом с русской аббревиатурой общепризнанную английскую.
Внутренняя норма доходности проекта (IRR)
Рассмотрим подробнее экономический смысл параметра
IRR. С формальной точки зрения 1RR— это то значение, коэффициента дисконтирования d, при котором обращается в ноль выражение для^У;
Яр а т
H(i+dy Н{\+d)
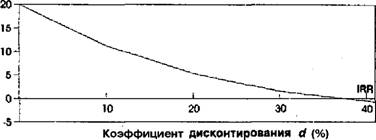
Задача 5. Фирма по продаже недвижимости предполагает купить две квартиры на общую сумму 350 млн. руб. Первую она хочет продать через год за 200 млн. руб., а вторую — через два года за 350 млн. руб. Определить NPV при различных коэффициентах дисконтирования и IRRпроекта.
Решение задачи представлено в таблице (табл. 10.7) и на графике (рис. 10.2).
|
Таблица 10.7
|
|
NPV
Рис. 10.2 |
Задача 6.
Инвестор вложил в предприятие по выпуску хлебобулочных изделий 12 млн. долл. Планируемые ежегодные поступления составят:
|
Таблица 10.8
|
Требуется определить внутреннюю норму доходности проекта.
Решение.
Решение задачи представлено в таблице (табл. 10.9.) и на графике (рис. 10.3)
|
Таблица 10.9
|
Экономическая суть 1RR — это уровень окупаемости средств, направленных на цели инвестирования. По своей природе IRR близка к различным процентным ставкам, используемым в других аспектах финансового менеджмента. Наиболее близкими величинами являются:
* действительная (реальная) годовая ставка доходности, предлагаемая банками по своим сберегательным счетам (т. е. ставка, рассчитанная по формуле сложных процентов за год); NPV
|
Рис.10,3 |
• действительная ставка процента по ссуде за год, рассчитанная по схеме сложного процента с учетом неоднократного погашения задолженности за год.
Иногда IRRназывают поверочным дисконтом, так как она позволяет найти граничное значение коэффициента дисконтирования, разделяющее инвестиции, с точки зрения инвестора, на выгодные и невыгодные.
' Для этого I ЯК сравнивают с тем уровнем окупаемости вложений, который инвестор выбирает для себя в качестве стандартного, и с учетом того, по какой цене сам инвестор получил капитал для инвестирования.
Если ставка сравнения — это ставка кредита, то NPV— это доход, который мы получаем после погашения кредита и процентов по нему. Если NPV< 0. то проект не способен выдержать кредит на таком уровне, и это эквивалентно тому, что JRR меньше ставки кредита.
Совершенно ясно, IRR может служить показателем «уровня риска» по проекту — чем больше 1RR превышает принятый фирмой барьерный коэффициент, тем больший запас прочности у проекта и тем менее страшны возможные ошибки при оценке величины будущих поступлений.
Как выбрать коэффициент дисконтирования?
Согласование коэффициента дисконтирования с инвестором — ключевой момент для принятия решения об инвестициях.
Задача очень простая и сложная, поскольку процедура дисконтирования дает принципиальную возможность учесть инфляцию, риски, а также возможность альтернативного использования капитала.
Подчеркнем, что речь идет именно о согласовании. Задача разработчиков бизнес-плана — доказать инвестору свою точку зрения, опираясь на известные методические подходы. Они изложены ниже.
Коэффициент дисконтирования можно согласовывать поэлементно или сразу — «интегрально», не разбивая его на составляющие При поэлементном согласовании используется метод цены капитальных активов. Ставка дисконта рассчитывается как сумма, каждое слагаемое которой учитывает отдельные составляющие дисконта. В эту сумму включены:
• номинальная (с учетом будущей инфляции) ставка по банковским кредитам;
• премия за риск вложений в малые предприятия;
• премия застраноиой риск;
• премия за закрытость компании, чьи акции покупаются инвестором;
• премия за относительный уровень специфических рисков рассматриваемого проекта по сравнению со средними рисками инвестиционных проектов того же типа.
Слово «премия» означает, что имеется некоторая базовая или безрисковая ставка, от которой все рассчитывается. Условно говоря, это и есть ставка, а все остальное — премии для инвестора то, что он согласен инвестировать в малые предприятия в данной стране, многого о них не зная, и т. д.
В США оценка «безрисковых вложений» — это вложение в государственные ценные бумаги. Их доходность — около 3,5% годовых, и они абсолютно ликвидные: их можно в любой момент поменять на доллары.
Определить номинальную безрисковую ставку банковского процента по фактической ставке доходности долгосрочных государственных облигаций можно в стабильной экономике, при достаточном числе операторов рынка (без явных лидеров).
В отдельные периоды возможно существование отрицательной реальной ставки ссудного процента (для инвестиционных расчетов это ни в коей мере не является нонсенсом — просто премии за инвестиционные риски должны закладываться в индивидуальную ставку дисконта).
За бездисковую ставку в российских условиях можно принять операций с теми товарами или когда конкурентный внутренний рынок сочетается с активным экспортом. Это — продовольственные и лекарственные товары первой необходимости, горюче-смазочные материалы.
В качестве примеров приведем конкретные средние цифры слагаемых дисконта по данным ведущих европейских стран и
США. Здесь номинальная годовая безрисковая ставка ссудного процента (складывающаяся из годовой инфляции в 3-4% и десятилетиями наблюдаемой средней годовой реальной безрисковой ставки также в 3-4%) составляет порядка 6-8%. Требуемая инвесторами премия за риск вложения в малый бизнес может достигать 5% годовых. Тоже касается и численной величины дополнительной премии. Дополнительную премию за страновой риск в индивидуальной ставке дисконта следуетучи - тывать независимо от того, является ли инвестор резидентом данной страны или иностранным резидентом. Премия за страновой риск оценивается на основании рейтингов чисто экспортно и может согласно имеющейся мировой статистике составлять 200-250% ставки дисконта, рассчитанной с учетом всех других (помимо странового риска) факторов.
Конкретной оценкой рисковости того или иного проекта служит оценка среднего отклонения
Разных ожидаемых доходностей проекта (или денежных потоков по нему в конкретные будущие периоды) от соответствующей средней ожидаемой доходности. В простейшем случае — среднее отклонение пессимистической и оптимистической оценок ожидаемой доходности от их среднестатистической величины. Таким образом, любые оценки рисков предполагают наличие достаточно подробной статистики отслеживания наблюдаемых величин — доходности акций, статистики поглощений и слияний различных компаний — всего того, для чего пишутся бизнес-планы и затеваются инвестиционные проекты. В России этого пока нет. Поэтому об индивидуальных ставках рисков нужно конкретно.
В качестве основы для оценки ставки дисконта «в целом» (или «интегрально») могут служить:
• при расчете в рублях — ставкаЦентрального банка РФ;
|
14-B5D |
|
209 |
• при расчете в валюте — ставка по валютному вкладу «до востребования» в Сбербанке РФ.