РАСЧЕТ ПРОЧНОСТИ ПО НОРМАЛЬНЫМ СЕЧЕНИЯМ ЭЛЕМЕНТОВ ПРЯМОУГОЛЬНОГО И ТАВРОВОГО ПРОФИЛЯ
Элементы прямоугольного профиля с одиночной арматурой (без предварительного напряжения) имеют следующие геометрические характеристики (рис. III.12):
АЬс = Ьх; Zb — H0—0,5дс, (III.8)
Где H0 и B —рабочая высота и ширина сечення.
Высоту сжатой зоны х определяют на основании равенства (III.3) из выражения
BxRb = RsAs. (III. 9)
Условие прочности, согласно выражению (III.4), имеет вид
M*ZRbbx(H0— 0,5*). (III. 10)
Удобно пользоваться также выражением моментов, взятых относительно оси, проходящей через центр тяжести сжатой зоны:
M<.RsAs(H0 — 0,5*). (III.11)
Формулы (III.9) и (III.10) или (III.11) применяют совместно. Они действительны при X<Lyh0, где ІУ определяют по выражению (11.42).
Коэффициент армирования
H=As/bh0 (III. 12)
И процент армирования р-ЮОс учетом соотношений (III.9) и £=X/HQ могут быть представлены так:
Li = LRb/Rs; = 100м - = 1 OOlRb/Rs. (III. 13)
Отсюда можно установить максимально допустимое содержание арматуры в прямоугольном сечении по предельным значениям из условия (11.42) (см. § II.6).
Если x>lyh0, то изгибающий момент вычисляют П0,| указаниям, приведенным в п. III.2.
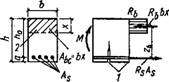
Рис. III.12. Прямоугольное сечение с одиночной арматурой и схема усилий при расчете прочности элемента по нормальному сечению
1 — нормальные трещины; 2 — Граница сжатой зоны
Из анализа выражений (111.10) и (111.11) следует, что несущая способность элемента может быть удовлетворена при различных сочетаниях размеров поперечного сечения элемента и количества арматуры в нем. В реальных условиях стоимость железобетонных элементов близка к оптимальной при значениях:
|і=1. .
Ц =0,3.
£=0,3. I =0,1.
0,4 0,15
} (HI. 14)
0,6
-для балок - для плнт
Прочность сечения с заданными B, As (материалы и момент М предполагаются известными) проверяют в такой последовательности: из выражения (III.9) находят высоту сжатой зоны х, проверяют ее по условию (III. 1) и затем пользуются выражениями (III.10) или (111.11).
Сечение считается подобранным удачно, если его несущая способность, выраженная по моменту, превышает заданный расчетный момент не более чем на 3—5 %.
Сечення подбирают по заданному моменту по выражениям (III.9) и (III.10) нлн (III.11) прн знаке равенства в инх.
В практике для расчета прямоугольных сечеиий с одиночной арматурой пользуются вспомогательной таблицей (III. 1). Формулы
(ШЛО) н (IM.11), преобразуя, приводят к виду
M = A0BhlRb-, As=Mlnh0Rs,
(III. 15) (III. 16)
Где
A0 = (Xlh0){ 1 -0,5*/fco) = |(1 -0,5|); T) = Z/H0 = 1 - 0,5X/H0 = 1 - 0,5Ј.
Из равенства (III. 15) находят выражение для определения рабочей высоты сечення
H0=VM/A0BRb.
По выражениям (III.17) и (III.18) для коэффициентов А0 и составлена табл. III.1. Пользование этой таблицей значительно сокращает вычисления.
Размеры сечений bah подбирают в следующем порядке: задаются шириной сечения b и рекомендуемым значением коэффициента | согласно (III.14), по которому из табл. III.1 находят коэффициент А0; по формуле (III. 19) вычисляют рабочую высоту сечения hQ, находят полную высоту H=HQ + A и по ней назначают унифицированный размер. Если данные размеры b и h не отвечают конструктивным или производственным условиям, их уточняют повторным расчетом.
Сечение арматуры As определяют в такой последовательности: вычисляют Л0 из выражения (III.15), для него по табл. III.1 находят т) и | и по формуле (III.16) определяют As, проверяя при этом условие (ІЦ.1).
Табл. III.1 может быть использована и для проверки 'прочности элемента. Вычисляют I=As/BhQ по известным данным о сечении, а также значение | по формуле (III.13), проверяя его по условию (III.1). Затем по | находят в табл. III.1 значение А0 и по формуле (III.15) вычисляют изгибающий момент, выдерживаемый сечением.
(III.17) (III. 18)
(III.19)
Элементы прямоугольного профиля с двойной арматурой. В практике могут встретиться случаи применения элементов с двойной арматурой (рис. III.13), хотя арматура в сжатой зоне менее эффективна, чем в растянутой.
145
Если в изгибаемом элементе предусматривается продольная арматура в сжатой (при действии нагрузки) зоне (с /?sc^400 МПа), учитываемая в расчете, то для предотвращения выпучивания продольных стержней поперечную арматуру ставят: в сварных каркасах на расстояниях не более 20D, в вязаных каркасах не более Bd
10-943
Таблица 111.1. Вспомогательная таблица для расчета изгибаемых элементов прямоугольного сечения, армированных одиночной арматурой
|
Г = х/н0 |
П = VA0 |
A |
Г = */Ao |
N = Vа» |
A |
|
0,01 |
0,995 |
0,01 |
0,37 |
0,815 |
0,301 |
|
0,02 |
0,99 |
0,02 |
0,38 |
0,81 |
0,309 |
|
0,03 |
0,985 |
0,03 |
0,39 |
0,805 |
0,314 |
|
0,04 |
0,98 |
0,039 |
0,4 |
0,8 |
0,32 |
|
0,05 |
0,975 |
0,048 |
0,41 |
0,795 |
0,326 |
|
0,06 |
0,97 |
0,058 |
0,42 |
0,79 |
0,332 |
|
. 0,07 |
0,965 |
0,067 |
0,43 |
0,785 |
0,337 |
|
0,08 |
0,96 |
0,077 |
• 0,44 |
0,78 |
0,343 , |
|
0,09 |
0,955 |
0,085 |
0,45 |
0,775 |
0,349 |
|
0,1 |
0,95 |
0,095 |
0,46 |
0,77 |
0,354 |
|
0,11 |
0,945 |
0,104 |
0,47 |
0,765 |
0,359 |
|
0,12 |
0,94 |
0,113 |
0,48 |
0,76 |
0,365 |
|
0,13 |
0,935 |
0,121 |
0,49 |
0,755 |
0,37 |
|
0,14 |
0,93 |
0,13 |
0,5 |
0,75 |
0,375 |
|
0,15 |
0,925 |
0,139 |
0,51 |
0,745 |
0,38 |
|
0,16 |
0,92 |
0,147 |
0,52 |
0,74 |
0,385 |
|
0,17 |
0,915 |
0,155 |
0,53 |
0,735 |
0,39 |
|
0,18 |
0,91 |
0,164 |
0,54 |
0,73 |
0,394 |
|
0,19 |
0,905 |
0,172 |
0,55 |
0,725 |
0,399 |
|
0,2 |
0,9 |
0,18 |
0,56 |
0,72 |
0,403 |
|
0,21 |
0,895 |
0,188 |
0,57 |
0,715 |
0,408 |
|
0,22 |
0,89 |
0,196 |
0,58 |
0,71 |
0,412 |
|
0,23 |
0,885 |
0,203 |
0,59 |
0,705 |
0,416 |
|
0,24 |
0,88 |
0,211 |
0,6 |
0,7 |
0,42 |
|
0,25 |
0,875 |
0,219 |
0,61 |
0,695 |
0,424 |
|
0,26 |
0,87 |
0,226 |
0,62 |
0,69 |
0,428 |
|
0,27 |
0,865 |
0,236 |
0,63 |
0,685 |
0,432 |
|
0,28 |
0,86 |
0,241 |
0,64 |
0,68 |
0,435 |
|
0,29 |
0,855 |
0,248 |
0,65 |
0,675 |
0,439 |
|
0,3 |
0,85 |
0,255 |
0,66 |
0,67 |
0,442 |
|
0,31 |
0,845 |
0,262 |
0,67 |
0,665 |
0,446 |
|
0,32 |
0,84 |
0,269 |
0,68 |
0,66 |
0,449 |
|
0,33 |
0,835 |
0,275 |
0,69 |
0,655 |
0,152 |
|
0,34 |
0,83 |
0,282 |
0,7 |
0,65 |
0,455 |
|
0,35 |
0,825 |
0,289 |
|||
|
0,36 |
0,82 |
0,295 |
(d — наименьший диаметр сжатых продольных стержней) и не более 500 мм.
Подставив АЬс и Zb из равенства (ПІ.8) в формулу (III.4), получим условие прочности изгибаемого элемента прямоугольного сечения, армированного двойной арматурой (при отсутствии Ар и Лр):
М < Rb Ъх (А0 - 0,5*) + Rsc A'S (H0 - а ), (III.20)
Ъ подставив АЬс в формулу (III.3), получим уравнение ^для определения положения границы - сжатой зоны
Rbxb = RsAs-RscAs. (III. 21)
При ЭТОМ имеется в виду соблюдение условия X^Lyho.
Если при одиночной арматуре оказывается, что *>£?Л), то арматура в сжатой зоне требуется по расчету. В этом случае нужно пользоваться расчетными формулами (III.6) и (III.7). В условиях применения бетонов
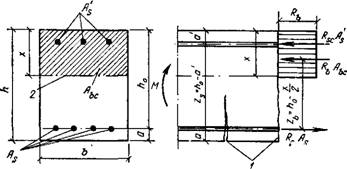
Рис. III.13. Прямоугольное сечение с двойной арматурой и схема усилий при расчете прочности элемента по нормальному сечению
1 — нормальные трещины; 2 — граница сжатой зоны
Класса ВЗО и ниже в сочетании с арматурой класса не выше A-III можно расчет производить по формуле
M^A^bbhl + R^A^hv-a), (III.22)
Где Av—A0 — нз табл. II1.1 для значения i = iv, вычисленного по формуле (11.42).
При подборе сечений с двойной арматурой по заданному моменту, классу бетона и классу стали возможны задачи двух типов.
Задача типа I. Заданы размеры & и Л. Требуется оп- ; ределить площадь сечения арматуры Asw. As.
Решение. Из условия (III.20), учитывая выражение ■(III.17), при X=Iyh0 находим
A's=(M-AyRb bhl)/Rsczf, (III.23)
А из уравнения (III.21)
As = A's RJRS + Ly Rb bh0/Ra. (Ill.24)
10* 147
Задача типа II. Заданы размеры сечения B и H и сжатая арматура A's. Определить площадь сечения арматуры Ав.
Решение. Из условия (111.20), принимая во внимание выражение (III.17), находим, что
Aa={M-RscAszs)/Rbbhl (III.25)
Если Ло^Лу, из табл. III.1 находим | и из равенства (III. 21)
А= A'SRJRs + Lhh0Rb/Rs. (III. 26)
Если А0>АУ, заданное количество As недостаточно.
При проверке прочности сечения (данные известны все) вычисляют высоту сжатой зоны из уравнения (111.21), затем проверяют условие (111.20).
Предварительно напряженные элементы с наличием в поперечном сечении арматуры A'Sp и A'S рассчитывают аналогично описанному, также с использованием выражений (II 1.3) и (III.4), но при сохранении всех членов.
Элементы таврового профиля. Тавровые сечения встречаются в практике весьма часто как в отдельных железобетонных элементах — балках (рис. III.14, а, б),
Так и в составе конструкций — в монолитных ребристых и сборных панельных перекрытиях (рис. III. 14,В, г,). Тавровое сечение образуется из полки и ребра.
В сравнении с прямоугольным (см. пунктир на рис. III.14, а) тавровое сечение значительно выгоднее, ибо при одной и той же несущей способности (несущая способность железобетонного элемента не зависит от площади сечения бетона растянутой зоны) расходуется бетона меньше вследствие сокращения размеров растянутой зоны. По той же причине более целесообразно тавровое се - , чение с полкой в сжатой зоне (рис. III.14,а), так как полка в растянутой зоне (рис. 111.14,6) не повышает несущей способности элемента.
Тавровое сечение, как правило, имеет одиночное армирование.
При большой ширине полок участки свесов, более удаленные от ребра, напряжены меньше. Поэтому в расчет вводят эквивалентную ширину свесов полки bд (рис. III. 14,В, г). Она принимается равной: в каждую сторону от ребра — не более половины расстояния в свету между ребрами с и не более '/в пролета рассчитываемого элемента, а в элементах с полкой толщиной hf <0,1 h без поперечных ребер или с ребрами при расстоянии между ними — более размера между продольными ребрами, вводимая в расчете ширина каждого свеса Ь( не должна превышать 6H /. Для отдельных балок таврового профиля (при консольных свесах полок) вводимая в расчет ширина свеса b д (рис. III.14, а) должна составлять:
При h'f>0,1 не более 6 h'f
При 0,05< H'F<0,1 H . . » » 3 Hf
При hf <0,05h свесы полки в расчете не учитывают.
При расчете тавровых сечений различают два случая положения нижней границы сжатой зоны: в пределах полки (рис. III.15, а) и ниже полки (рис. 111.15,6).
Нижняя граница сжатой зоны располагается в пределах полки, т. е. x^Zhj в сечениях с развитыми свесами. В этом случае тавровое сечение рассчитывают как прямоугольное с размерами B/ и H0 (рис. III.15, а), поскольку площадь бетона в растянутой зоне на несущую способность не влияет.
Расчетные формулы (для элементов без предварительного напряжения):
Rbb'fx=RsAis (III. 27)
M<Rbbf(h0 — 0,5*) (111.28)
Или
M<CAaRbb)Hl, <Ш.29>
Где Ац — коэффициент из табл. III.1.
Нижняя граница сжатой зоны размещается ниже полки, т. е. x>hj, в сечениях со слаборазвитыми свесами. В этом случае сжатая зона сечения состоит из сжатой зоны ребра и свесов полки.
Положение нижней границы сжатой зоны определяется из уравнения
ЯД^^г + Я^ — (Ш. ЗО)
О) Я
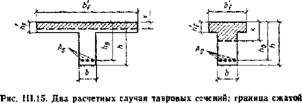
Зовы проходит
А—в пределах полки; 6 — ниже полки
Условие прочности при моментах, вычисляемых относительно оси, нормальной к плоскости изгиба и проходящей через точку приложения равнодействующей усилий в растянутой арматуре, имеет вид
М с Rb Ьх (h0 — 0,5*) + R6 (bj—b) h'f (Л0 — 0,5/iJ}. (Ш.31)
Для тавровых сечений должно соблюдаться условие
Ориентировочно высота тавровой балки может быть определена по формуле (из опыта проектирования)
H = (7 ... (Ш.32)
Где H — см; М, кН-М. Ширину ребра о5ачно принимают равной
Ь= (0,4 ... 0,5}Л. (1IL33)
Размеры полки и ft/ чаще всего известны из компоновки конструкции. Сечение арматуры во расчетному моменту определяют в зависимости от расчетного слу -
* чая. Если нейтральная ось проходит в пределах полки, то Л5 находят из расчета сечения как прямоугольного с одиночной арматурой при размерах B T и H0, используя табл. III.1.
Расчетный случай таврового сечения может быть определен по следующим признакам:
Если известны все данные о сечении, включая Л s, то при
Rs А5 < Rb B'F H'F (III.34)
Граница сжатой зоны проходит в полке; при обратном неравенстве она пересекает ребро;
Если известны размеры сечения Bf, Hf, B, H и задан расчетный изгибающий момент, но /4S неизвестно, то при
M<Rbb'FH'F(H0-0,5,) (III.35)
Граница сжатой зоны проходит в полке; при обратном неравенстве она пересекает ребро.
Для случая, когда граница сжатой зоны проходит ниже полки, формулы (II 1.31) и (III.30) можно преобразовать с учетом соотношений х=Уг0 и (III.17):
Я Ag = ІRbbh0 + Rb(B'F-B)Hf-, (III.36)
M < A0 Rb bh + Rb (T(f - b)hf(h0- 0,5H), (III.37)
Где коэффициенты A0 принимают по табл. III. 1.
Эти формулы можно использовать для подбора сечения. Если требуется определить Лї, то из (III.37) вычисляют
А0= [M-Rb(B'!-B)H)(HQ-0,5Hf)]/Rbbhl, (III.38)
Затем из табл. II 1.1 находят соответствующее вычисленному Л0, и, согласно формуле (III.36),
As = [№0 + (B'f - Ь) Hf] Rb/Rs. (III.39)
Если необходимо проверить прочность сечения при всех известных данных, то расчетный случай лучше установить по формуле (II 1.35) и затем (если граница сжатой зоны ниже полки) по выражению (III.30) вычислить высоту сжатой зоны х, после чего воспользоваться формулой (III.31).
§ III.4. РАСЧЕТ ПРОЧНОСТИ ЭЛЕМЕНТОВ ПО НОРМАЛЬНЫМ СЕЧЕНИЯМ ПРИ КОСОМ ИЗГИБЕ
В практике наиболее часто применяют элементы с поперечными сечениями, имеющими по крайней мере одну ось симметрии. Если при этом плоскость действия внешнего изгибающего момента (от заданных нагрузок и опорных реакций) занимает наклонное положение относительно плоскости симметрии сечения, то элемент окажется подверженным косому изгибу.
Элементы, испытывающие косой изгиб, в общем случае могут быть армированы продольными стержнями с размещением их по всему периметру сечения.
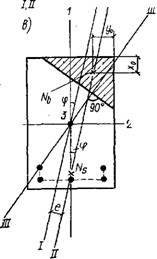
Если элемент подвержен косому изгибу с постоянным положением плоскости действия внешнего изгибающего момента, то в таком элементе продольные стержни арматуры целееообразно размещать сосредоточенно, т. е. только в растянутой зоне поперечного сечения, по возможности дальше от границы сжатой зоны. Рассмотрим далее косоизгибаемые элементы прямоугольного попе - ' речного сечения, которые применяют наиболее часто в практике (рис. III.16).
В результате расчета конструкции определяют значение внешнего изгибающего момента и положение плоскости его действия. Обычно эта плоскость проходит через геометрическую ось элемента, принятую в расчетной схеме конструкции. Естественно равнодействующую усилий Ns в стержнях растянутой арматуры расположить в той же плоскости (рис. III.16, а, б). Тогда и равнодействующая сжимающих напряжений Ns в бетоне сжатой зоны должна разместиться в той же плоскости.
Но равнодействующая растягивающих усилий Ns Может быть принята расположенной и вне плоскости действия внешнего момента, на некотором расстоянии е (вследствие расчета того же элемента при другой комбинации нагрузок или по условиям унификации и т. д.). В этом случае равнодействующая Nb напряжений в бетоне сжатой зоны займет положение в плоскости, параллельной плоскости действия внешнего момента (рис. III.16, е).
Сжатая зона бетона может иметь форму треугольника или трапеции. Усиление ее арматурой обычно нерационально.
Прочность косоизгибаемого элемента по нормальному
Сечению рассчитывают в плоскости III—III, перпендикулярной границе сжатой зоны, с размерами сечения х (высота сжатой зоны) и Л0 по условию
М cos (а — (Ц) < Rb Abc Гъ (III. 40)
I ж
(обозначения а, ф и Zb — см. на рис. III.16, а).
Площадь бетона сжатой зоны АЬс определяют из равенства значений равнодействующих в растянутой и сжатой зонах
RsAs = RbAbc - (III.41)
В формулах (111.40) и (111.41) напряжение во всех стержнях арматуры принято одинаковым, поскольку они расположены приблизительно на одном расстоянии от границы сжатой зоны.
Положение границы сжатой зоны определяют с учетом того, что плоскость внутренней пары сил или совпадает с плоскостью действия внешнего изгибающего момента, или ей параллельна. Остальные требования, предъявляемые к расчету изгибаемых элементов,— соблюдение условия l=x/hQ<ly, учет повышенного сопротивления высокопрочной арматуры — сохраняются и для косого изгиба.
Косоизгибаемые элементы с отмеченными особенностями можно рассчитывать также по сопоставлению проекции внешнего момента и момента М внутренней пары сил на плоскость симметрии 1:
Mt=M cos ф < As Rs (h0i - *0). (Ill. 42)
Определение размеров треугольной сжатой зоны (рнс. III. 16,А). Учтем соотношение
М2/Мі — Л8 Rs (й02 - У)/As Rs (Лох - X) = (Ло2 - Y0)(Hoi — *0),(III.43)
Где М2 — проекция изгибающего момента, действующего в плоскости J, на плоскость симметрии 2.
Обозначим
С0= M2/M! = tgq> (III. 44)
И примем во внимание, что при треугольной форме сжатой зоны
АЬс= 1/2хіУі, Х0= 1/3*! и у0= L/Зуі. (111.44а)
Выражения (II 1.41) и (111.43) приводят к уравнению
+ 3 - V) - 2 Ag - = О, (III. 45)
Из которого находим значение Х{. Затем из выражения (111.41) вычисляем у І.
Если х получается отрицательным или Yi>B, это значит, что сжатая зона имеет не треугольную, а трапециевидную форму.
Определение размеров сжатой зоны трапециевидной
Формы (рис. III. 16,6). Размеры сжатой зоны Х и х2 могут быть определены из соотношения
As tfs = 0,5 (*1 + Х2) BRb (III.46)
И равенства (111.43), в котором
У0 = (BJ3)(Xl + 2х2)/(х1 + х2У, х0 = 1/з (4 + ^ *2 + х22)!{х1 + х2)
Эти выражения приводят к уравнению 4 + (B/C0 - Ci} Xl + сх (3HJC0 - 2B/CQ - 3H01 + С,) = 0, (III .48) Где
C1^2AsRslbRb. (III.49)
Эти формулы справедливы и в том случае, когда плоскость положения равнодействующих усилий в растянутой и сжатой зонах сечения параллельна плоскости действующего изгибающего момента (рис. III.16, в). ^