Железобетон

Деформации бетона при многократно повторном дей­ствии нагрузки

Многократное повторение циклов загру - жения и разгрузки бетонной призмы приводит к посте­пенному накапливанию неупругих деформаций. После достаточно большого числа циклов эти неупругие де­формации, соответствующие данному уровню напряже­ний, постепенно выбираются, ползучесть достигает свое­го предельного значения, бетон начинает работать упру­го. На рис. 1.13 показано, как с каждым последующим циклом неупругие деформации накапливаются, а кривая Оь—е», постепенно выпрямляясь, становится прямой, ха­рактеризующей ушругую работу. Такой характер дефор­мирования наблюдается лишь при напряжениях, не

3* 35

Превышающих предел выносливости Ob^Rr. При боль­ших напряжениях после некоторого числа циклов не­упругие деформации начинают неограниченно расти, что приводит к разрушению образца, при этом кривизна линии оь—еь меняет знак, а угол наклона к оси абсцисс последовательно уменьшается.

При вибрационных нагрузках с большим числом по­вторений в минуту (200—600) наблюдается ускоренное развитие ползучести бетона, называемое виброползуче­стью, или динамической ползучестью.

Предельные деформации бетона перед разрушением — предельная сжимаемость ъиь и предельная растяжимость Еиы — зависят от прочности бетона, его класса, состава, длительности приложения нагрузки. С увеличением клас­са бетона предельные деформации уменьшаются, но с ростом длительности приложения нагрузки они увеличи­ваются. В опытах при осевом сжатии призм наблюдается предельная сжимаемость бетона еы&= (0,8...3) 10~3, в среднем ее принимают равной: еыг> = 2-10_3. В сжатой зоне изгибаемых элементов наблюдается большая, чем у сжатых призм, предельная сжимаемость, зависящая от формы поперечного сечения и относительной высоты сжатой зоны, гиь— (2,7...4,5) Ю-3; при уменьшении ши­рины поперечного сечения книзу и в тавровых сечениях Еиь уменьшается, а при уменьшении относительной вы­соты сжатой зоны Еиь увеличивается. Она зависит также от насыщения продольной арматурой.

Сжимаемость бетона значительно возрастает, если при его загружении происходит пропорциональное воз­растание деформаций (см. рис. 1.9); в этом случае на диаграмме напряжения — деформации появляется ни­сходящий участок. Учет работы бетона на нисходящем участке диаграммы имеет существенно важное значение для расчета ряда конструкций.

Предельная растяжимость бетона в 10—20 раз мень­ше предельной сжимаемости, в среднем ее принимают равной: еыг>г= 1,5-Ю-4; бетоны на пористых заполните­лях имеют несколько большую предельную растяжи­мость. Предельная растяжимость бетона существенно влияет на сопротивление образованию трещин в растя­нутых зонах железобетонных конструкций.

Модуль деформаций и мера ползучести бетона

Начальный модуль упругости бетона при сжатии Еь соответствует лишь упругим деформациям, возникающим при мгновенном загружении, геометрически он опредедя - ется как тангенс угла наклона прямой упругих дефор­маций (рис. 1.14)

Еь = tga0. (Ь7)

Модуль полных деформаций бетона при сжатии Еь Соответствует полным деформациям (включая ползу­честь) и является величиной переменной; геометрически он определяется как тангенс угла наклона касательной к кривой аь—Еь в точке с заданным напряжением

= = Tea. (1.8)

Deb

Деформацию бетона можно было бы находить с по­мощью переменного модуля деформаций интегрировани­ем функции

Eft = J(l /E'b)dab.

Однако такой способ определения деформаций за­труднителен, так как аналитическая зависимость для Еь неизвестна. Поэтому для расчета железобетонных конструкций пользуются средним модулем, или модулем упругоплаетичности бетона, представляющим собой тан­генс угла наклона секущей к кривой оь—еь в точке с за­данным напряжением:

Е'ь= tgar. (1.9)

Поскольку угол а меняется в зависимости от напряже­ний, модуль упругоплаетичности—также переменная величина, меньшая, чем начальный модуль упругости.

Зависимость между начальным модулем упругости бетона и модулем упругоплаетичности можно установить, если выразить одно и то же напряжение в бетоне о» че­рез упругие деформации ее и полные деформации еь:

АЪ = ееЕЬ*=еЬЕ'ь'

Отсюда

ЕЬ^ЕЬ, (1.10)

Где %ъ = ее/вь — коэффициент унругопластических деформаций бетона, равный отношению упругих деформздий к полным. По дзнным Oflbl"
тов, коэффициент Кь изменяется от 1 (при упругой работе) до —0,15. С увеличением уровня напряжений в бетоне оь/Яь н длительности действия нагрузки t коэффициент fa уменьшается. Значение fa(T) мо­жет определяться по специальным опытным данным нли по средним опытным диаграммам оь — еь (рис. 1.15).

При изгибе железобетонных элементов для бетона сжатой зоны (по данным опытов)1 Е ь может быть на 15—20,% больше, чем при осевом сжатии.

При растяжении элементов модуль упругопластич - ности бетона

»

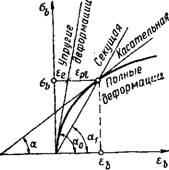
Рис. 1.18. Диаграммы въ—Е» при различном времени загру - жении бетона

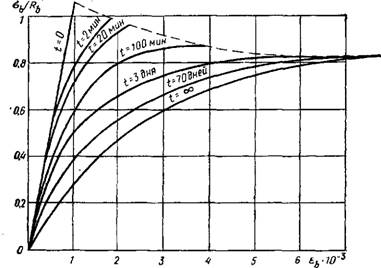
Рис. 1.14. К определению МОДУ" ля деформации бетона

Еы=1ыЕъ, 5(1.11)

Где Яб( = еЄ(/еб« — коэффициент упругопластических деформаций бе­тона при растижении. Если растигивающее напряжение в бетоне приближаетси к временному сопротивлению — осевому растяжению Obt->-Rbt, среднее опытное значение %ы = 0,5.

Предельная растяжимость бетона в зависимости от временного сопротивления растяжению

Начальный модуль упругости бетона при сжатии и растяжении Еь может быть определен из специальных испытаний призм при низком уровне напряжений: Ob/Rb^0,2. Существуют различные эмпирические фор­мулы, в которых устанавливается зависимость между на­чальным модулем упругости и классом бетона. В нормах для тяжелого бетона естественного твердения принята эмпирическая формула

Еь = 550 0005/(270 + В). (1.13)

Значение Еь при тепловой обработке бетона снижа­ется на 10 %, при автоклавной — на 25 %. Бетоны на пористых заполнителях, как более деформативные, об­ладают в 1,5—2 раза меньшим значением начального модуля упругости. Различные эмпирические формулы основаны на зависимости между начальным модулем упругости, средней плотностью и кубиковой прочностью бетона. Так, например, отношение начальных модулей упругости легкого бетона на пористых заполнителях и тяжелого бетона может определяться по эмпирической формуле

Ј=(Vi/V)3/2. (1-14)

Где i — средняя плотность бетоиа на пористых заполнителях и тя­желого бетона прн одном и том же классе.

Значения начального модуля упругости бетона при сжатии и растяжении в зависимости от вида бетона и его класса приведены в прил. IV.

Модуль сдвига бетона

Gb = Јb/[2(1 +v)]; (1.15)

При коэффициенте поперечных деформаций v = 0,2 он принимается равным 0,4 Еь.

Мера ползучести бетона при сжатии Сь применяется для определения деформации ползучести в зависимости от напряжения в бетоне

Ері = Сьаь. (1.16)

Из выражения (1.16)

Сь = ЕРі/аь = ЕРі/ее Еь

Или

Сь = ф/£ь> (1.17)

Где <р — характеристика ползучести бетона,

Ф = грі/8е = (1 — lb)/h - (Іл7а)

Мера ползучести бетона зависит от его класса, уров­ня напряжений и является переменной во времени.

Для аналитического выражения линейной ползучести бетона приняты математические модели и построены различные теории ползучести, наибольшее признание из которых получила наследственная теория старения. Тем не менее, пользоваться полученными по этой теории уравнениями для практических расчетов железобетон­ных конструкций с учетом длительных процессов за­труднительно, особенно при сложном напряженном со­стоянии (внецентренном сжатии, изгибе предваритель­но напряженных элементов и др.) и высоких уровнях напряжений. Поэтому на практике прибегают к различ­ным приемам расчета, основанным на использовании ЭВМ и применении дискретных моделей С большим чис­лом стерженьков-элементов, работающих на осевое сжа­тие или осевое растяжение в каждый момент времени линейно, в которых на каждой ступени загрузки прини­мается своя зависимость аь—еь по средним опытным ди­аграммам.