Вечный двигатель

Тепловой насос — чудо или не чудо?

Напомним принцип действия теплового насоса[35] (о нем уже шла речь в гл. 3). Независимо от типа и конструкции это устройство выполняет, как правило, одну функцию — отбирает теплоту Qo c от окружающей среды при ее тем­пературе Г0 с и отдает теплоту при более высокой темпе­ратуре Тг в отапливаемое помещение или для подогрева в каком-либо техническом устройстве. Такой процесс пере­хода теплоты сам по себе происходить не может — это

Запрещено вторым законом термодинамики. Поэтому для обеспечения работы тепловых насосов необходима опреде­ленная затрата эксергии. Чаще всего для привода теплового насоса используется электроэнергия.

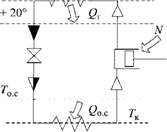
Принципиальная схема наиболее простого (парокомпрес - сионного) теплового насоса показана на рис. 4.4.

Рабочее тело в парообраз­ном состоянии сжимается АЛЛ Гг компрессором (поэтому уста - -

Новка и называется пароком - прессионной). Нагревшийся при сжатии пар охлаждается и переходит в жидкое со­стояние в конденсаторе; при этом от него при повышен­ной температуре Тт отво­дится к потребителю (напри-

Мер, в нагреваемое помеще­ние) теплота QT. Получен­ная жидкость расширяется в Рис. 4.4. Схема теплового насоса дросселе, и ее давление сни­жается. При этом часть жидкости испаряется и ее тем­пература падает до Тк, несколько более низкой, чем тем­пература окружающей среды Го с. В испарителе холодная жидкость, отнимая теплоту Qo c у окружающей среды, пол­ностью испаряется и снова поступает в компрессор; цикл замыкается.

Возьмем для примера конкретные показатели работы насоса, близкие к тем, которые встречаются на практике.

Чтобы отапливать помещение и поддерживать в нем температуру +20 °С, конденсирующееся рабочее тело долж­но иметь температуру Тг, скажем, 50 °С (323 К). Пусть тем­пература окружающей среды Го с будет —10 °С или 263 К (зимние условия). Для того чтобы рабочее тело могло ки­петь в испарителе, отнимая теплоту от среды, оно должно быть несколько холоднее ее. Примем температуру кипения

Тк = -20 °С (253 К).

Примем также, что отдаваемая в помещение тепловая мощность Qr составляет 5 кВт, а подводимая к компрес­сору N = 2 кВт. Тогда по энергетическому балансу теп­ловая мощность Qo c, отбираемая от окружающей среды, составит 5 — 2 = 3 кВт. Пользуясь этими данными, можно легко рассчитать все энергетические характеристики те­плового насоса. Чтобы закончить рассмотрение баланса,

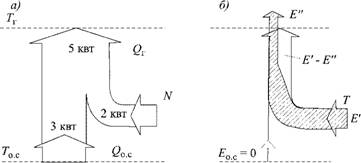
Характеризующего систему с позиций первого начала тер­модинамики, определим отношение полученной теплоты QT к затраченной электрической работе. Эта величина, на­зываемая тепловым или отопительным коэффициентом, здесь имеет значение /і = 5/2 = 2,5. Следовательно, на 1 кВт электрической мощности, подводимой к компрес­сору, в помещение отдается 2,5 кВт тепловой мощности. Тот факт, что /і > 1, вызывает восторг у сторонников «энергетической инверсии». Называя /і коэффициентом полезного действия (вместо теплового коэффициента), они утверждают, что он (КПД) превышает 100 %, так как «кон­центрирует энергию», взятую из окружающей среды. Дей­ствительно, 3 кВт берутся из окружающей среды. Диа­грамма на рис. 4.5 наглядно показывает этот энергетиче­ский баланс в виде полосового графика, где ширина ка­ждой полосы пропорциональна соответствующему потоку энергии.

Теперь займемся анализом этого же теплового насоса с позиций второго закона термодинамики. Начнем с энтро­пии. В этом простом примере ее легко подсчитать. Дей­ствительно, отдаваемая энтропия

S" = Qr/Tr = 5/323 = 0,015 кВт/К, а подводимая

S' = Qo. c/Го. с = 3/253 = 0,012 кВт/К.

Больше никакая энтропия к тепловому насосу не подво­дится, так как высокоорганизованная электроэнергия без­энтропийна. Значит, со вторым законом здесь все в по­рядке: отводимая энтропия S" больше подводимой S'. Не­обратимые, реальные процессы в тепловом насосе приво­дят, естественно, к ее возрастанию на AS = 0,003 кВт/К. Значит, действие теплового насоса никоим образом не противоречит второму закону термодинамики: энтропия растет. А как же с КПД и «концентрацией» энергии?

Займемся этим и рассмотрим работу теплового насоса посредством составления и анализа его эксергетического баланса. В такой баланс, так же как и в энергетический, должны входить три члена, соответствующих энергетиче­ским потокам. Однако один из них будет равен нулю, поскольку эксергия потока теплоты Qo. c> отбираемой из окружающей среды при Го с, равна нулю (по формуле Кар­но). Следовательно, в систему эксергия поступает только с электроэнергией (заштрихованная полоса соответствует эксергии); подсчитать ее легко, поскольку высокоорганизо­ванная электрическая энергия полностью работоспособна. Значит, поступающая эксергия Ef = 2 кВт.

Отводимая эксергия представляет собой эксергию отво­димой теплоты QT она равна Е" = = 0,929 кВт.

Остальная эксергия Е' - Е" = 2 - 0,929 = 1,071 кВт по­теряна вследствие необратимости. Эксергетический КПД теплового насоса составит

0 929

Г]е = — = 0,46, или 46%.

Соответствующая эксергетическая диаграмма показана на рис. 4.5, б. Из нее видно, что эксергетический баланс дает наиболее полную информацию об энергетических пре­вращениях в системе. Он показывает, сколько полезной, работоспособной энергии затрачено, сколько получено и сколько потеряно вследствие необратимости, вызванной термодинамическим несовершенством процесса. КПД по­казывает (в отличие от теплового коэффициента) степень приближения процесса к идеальному: только 46% под­веденной эксергии «пошли в дело». Остальные 54% по­теряны. Несмотря на то, что КПД существенно меньше 100 %, такой нагрев более эффективен, чем непосредствен­ное электрическое или печное отопление; отсюда и стрем­ление к использованию теплоты от теплоэлектроцентралей (ТЭЦ) и теплонасосных установок (ТНУ).

Посмотрим, «сколько стоит» в энергетическом смысле теплота при получении ее разными путями. Приведем та­кой расчет для тех же условий (То с = —10 °С, температура отопительного прибора Тг = 50 °С) применительно к элек­тропечи. При затрате электроэнергии (т. е. эксергии) 1 кВт она даст, естественно, 1 кВт теплоты, Q = 1. Отсюда экс­ергия теплоты будет 132 32363 = ОД86 кВт. Следовательно, КПД электропечи Tje = 18,6%. Такой же примерно КПД будет иметь и обыкновенная печь, так как эксергия топ­лива (например, угля) практически равна теплоте, которая в идеальном процессе горения может быть из него полу­чена. Таким образом, из 1 кВт теплоты, так же как и в электропечи, будет получено 0,186 кВт эксергии теплоты. КПД отопления с ТЭЦ составляет около 40-45 %, т. е. при­мерно такой же, как и у ТНУ.

Подсчитаем в заключение, сколько теплоты Q для отоп­ления при этих условиях (Тг = 50 °С) сможет дать 1 кВт электроэнергии в идеальном тепловом насосе. При г]е = 1 (т. е. 100%) эксергия полученной теплоты будет равна

1 кВт. Получим

323 263 1

1 — Q =------------------ , отсюда С) =--------------- = 5, 38 кВт.

^ 323 ' ^ 0,186

Вот сколько теплоты может дать идеальный тепловой на­сос!

Рассмотрение теплового насоса, проведенное выше, по­казывает, что это очень хорошее и полезное на своем месте устройство. Однако нет никаких оснований считать, что он обладает чудесными свойствами. Тепловой насос приносит пользу, но, как всякая реальная установка, увеличивает эн­тропию, превращая более упорядоченную, организованную электроэнергию и менее организованную теплоту Qo c в еще менее организованный тепловой поток с большей эн­тропией. Никакой «концентрации» (если понимать ее как повышение качества энергии) поэтому он не производит. Тепловой коэффициент /І у него всегда больше единицы, но никакого чуда в этом нет, /і, — это не КПД. Легко по­казать, что /і может иметь намного большие значения, чем

2 или 3, рассмотрев его изменение при разных внешних условиях.

Возьмем для примера тепловой насос с высоким, но вполне достижимым КПД Tje — 0,5 и подсчитаем его те­пловой коэффициент при разных значениях верхней тем­пературы Т2 и при Т0 с = 293 К (20 °С). Примем значения Т2 равными 25, 50, 100, 150, 200 и 250 °С (по шкале Кель­вина соответственно 298, 323, 373, 423, 473 и 523 К). Тогда при затрате мощности N = 1 кВт мы получим на верхнем уровне при выбранном КПД эксергию теплоты Eq = 0,5 кВт. Отсюда можно определить Qr, пользуясь известным соотношением

Тг — То с

L = Eq — QT-

Тт

Откуда

Т т

Qr = EqrTi ^ =0,5; г

'Тг-То. с ' Тг — 293

Отсюда видно, что значения i даже для реальной ма­шины (не говоря уже об этих значениях для идеальной ма­шины, указанных в скобках) могут достигать в соответству­ющих температурных интервалах 200-300 (или, если счи­тать, как делают некоторые, в процентах, 20 000-30 000 %). Действительно чудо! Есть от чего прийти в восторг. Затра­тил 1 кВт, а получил 290!

Однако прежде чем бить в литавры, посмотрим, какая это теплота. Она характеризуется температурой всего на 5 °С выше окружающей среды. Ее коэффициент работо­способности меньше 0,002; это означает, что если такой теплоты мы имеем на «тепловой рубль», то его настоящая стоимость в валюте полностью организованной энергии — в работе — меньше 0,2 коп. По мере «улучшения» те­плоты, повышения ее температуры Тг ее качество растет, а значение /і сильно падает.

Таким образом, большие числа /і, свидетельствуют не о чудесном извлечении «тепловой энергии» из окружающей среды, а лишь о том, что получаемая теплота очень низкого качества.

Тем не менее ажиотаж вокруг теплового насоса, осно­ванный на больших значениях коэффициента преобразова­ния, не проходит. Примером может служить статья Г. Ли - хошерстных «В поисках энергии» [3.10], который, опира­ясь на «необычные свойства» тепловых насосов, дающих КПД, «в десятки и сотни раз превосходящие единицу», выдвинул оригинальную энергетическую идею. Он счи­тает необходимым провести работы не только по «теоре­тическим исследованиям проблемы», но и «конечно же, по разработке экономичных способов превращения выда­ваемой ими теплоты в электрическую энергию». Другими словами, он предлагает превращать в электроэнергию ту самую низкокачественную теплоту, о которой мы говорили выше.

Посмотрим, к чему привела бы реализация этого пред­ложения.

На тепловых электростанциях получают электроэнер­гию с КПД примерно 40%. Далее эта электроэнергия должна в тепловом насосе преобразоваться в теплоту. Возь­мем для насоса высокий КПД — 0,5 і. Затем используем эту теплоту для получения электроэнергии. Примем КПД такого преобразования тоже достаточно высоким — 0,4 (40%).

В результате конечная электроэнергия по способу Ли - хошерстных будет получаться с КПД 0,4 • 0,5 • 0,4 = 0,08, или 8 %, т. е. в 5 раз худшим, чем просто на электростан­ции!

Вот к чему приводит тезис «теплота есть теплота неза­висимо от температуры».

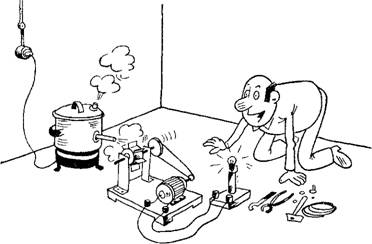
В журнале «Изобретатель и рационализатор» была по­мещена в разделе «перпетомобиль» карикатура, показанная на рис. 4.6. Если сравнить только что описанную идею со схемой, изображенной на ней художником, то бросается в глаза их удивительное сходство; нужно только заменить электроплитку на тепловой насос. Едва ли автор рисунка мог подумать, что найдутся люди, всерьез предлагающие такую идею.

На примере теплового насоса можно видеть, к чему при­водит непонимание второго закона термодинамики. Он, ко­нечно, мешает «свободному творчеству», и у изобретателей

Коэффициенты преобразования при этом будут достаточно боль­шими в соответствии с таблицей, но это, как мы видели, не меняет дела.

Ррт-2 нет более пламенного желания, чем добиться его ис­чезновения. Поскольку это не удалось, остается мечтать. Именно так поступил канд. техн. наук Н. Заев, опубликовав статью под названием «Энергетические искушения» [3.5] и обрисовав перспективы энергетики «за барьером XX ве­ка». Прежде чем перейти в следующей главе к рассмотре­нию современных ррт-2, стоит процитировать отрывки из этой статьи, представляющей некоторый «антитермодина­мический манифест» «Только у букинистов можно купить обветшавшие тома нашей термодинамики. Она осталась не у дел. По мере развития термодинамики настоящей, преж­ние курсы сначала перестали читать, а потом и издавать. Настоящая термодинамика элементарно объясняет то, что в прежние времена обосновывали нагромождением начал, теорем, формул... Нет больше энтропии, энтальпий, экс - ергий и тому подобных загадочно звучащих терминов...».

Этот набор негативных лозунгов сводится по существу к призыву свободы от науки: даешь такую термодинамику, которая «элементарно объясняет» все, что надо, без всяких там «начал, теорем, формул».

Но поскольку новой «элементарно объясняющей» тер­модинамики пока нет, а старая существует не только у букинистов, мы перейдем к рассмотрению истории и со­временных проектов ррш-2 на основе существующей тер­модинамики.

Однако перед этим было бы полезно уделить некоторое внимание выяснению вопроса, который неизбежно возни­кает при рассмотрении последнего этапа истории ррш, — почему все же изобретают ррш-2? Мы перебрали в гл. 3 и 4 все доводы сторонников «энергоинверсии» — и фило­софские, и космологические, и биологические, и техниче­ские... Весь материал, приведенный в этих главах, одно­значно показывает, что нет ни единого довода или факта, который всерьез может быть принят как доказательство возможности существования ррш-2. И тем не менее упор­ные попытки обосновать и создать ррш-2 продолжаются. Выдвигаются, как мы увидим дальше, и новые теоретиче­ские концепции с мудреными названиями вроде «струк­туры Прометея» или даже «структуры Хоттабыча», созда­ются новые проекты... При мало-мальски серьезном ана­лизе оказывается, что все они основаны на тех же ошибках, о которых уже подробно говорилось. В чем же дело?