ТОНКОПЛЕНОЧНЫЕ. СОЛНЕЧНЫЕ ЭЛЕМЕНТЫ. НА ОСНОВЕ КРЕМНИЯ

Модель энергетического спектра носителей заряда

Несмотря на то, что до настоящего времени единой теории некристалли­ческих материалов не существует, многие оптические и фотоэлектрические свойства могут быть объяснены исходя из представлений о зонном распреде­лении энергетических состояний в аморфных полупроводниках [25]-[30], [33]. Однако отсутствие дальнего порядка приводит к существенному отли­чию структуры энергетических зон кристаллических и неупорядоченных по­лупроводников. В связи с этим перед рассмотрением собственно оптического поглощения в аморфных полупроводниках необходимо представить особен­ности структуры энергетических зон в неупорядоченных полупроводниках. В них отсутствует дальний порядок, поэтому основные положения зонной теории кристаллов в данном случае оказываются неприменимыми.

В начале 50-х годов А. Ф. Иоффе сформулировал эмпирическое прави­ло, из которого следует, что за полупроводниковые свойства в материалах отвечает ближний порядок. Сохранение ближнего порядка в неупорядо­ченных полупроводниках объясняет зонный характер распределения в них энергетических состояний.

Аморфные материалы, так же как идеальные полупроводники, имеют делокализованные состояния, благодаря которым электроны и дырки могут свободно перемещаться. Однако отсутствие дальнего порядка приводит к тому, что для них длина свободного пробега значительно ниже, чем в кри­сталлическом материале. Когда эта зависящая от энергии длина свободного пробега становится сравнимой с межатомным расстоянием, носители заряда локализуются.

Исследования об электронной структуре аморфных полупроводников и предположение о наличии хвостов зон в некристаллических полупровод­никах были представлены А. И. Губановым в 1963 г. [34].

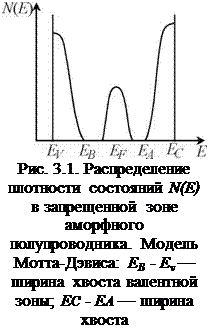Конкретные расчеты и оценка реальных неупорядоченных систем бы­ли проведены в работах Мотта [26]-[28], [30], [35]. Согласно идеям Мотта в неупорядоченных полупроводниках должны существовать хвосты локали­зованных состояний на краях валентной зоны и зоны проводимости, а также граничные энергии, разделяющие локализованные состояния от распро­страненных [35]. На основе этих исследований было разработано несколько моделей структуры энергетических зон в не­упорядоченных полупроводниках. Согласно Мотту и Дэвису (рис. 3.1) хвосты локализо­ванных состояний довольно узкие и распро­страняются в запрещенную зону на несколь­ко десятых долей электронвольта. Уровень Ферми закрепляется в узкой зоне компенси­

зоны пповопимости

разупорядочения аморфного полупроводника они увеличиваются и в модели Мотта-Дэвиса имеют экспоненциальное распределение. Пик глубоких со­стояний описывается гауссовым распределением.

В идеальном кристалле энергетические состояния не могут существо­вать внутри запрещенной зоны, а в аморфном полупроводнике имеется неко­торое множество локализованных состояний. Носители могут перемещаться с локализованных состояний только в том случае, если они получат дополни­тельную, значительную энергию. В результате отношение подвижностей но­сителей заряда по делокализованным и локализованным состояниям превы­шает три порядка. Поэтому диапазон энергий от Ey до Ec называется в аморфных полупроводниках щелью подвижности. Именно этот аналог за­прещенной зоны, энергетической щели в кристаллических полупроводниках и обеспечивает наличие полупроводниковых свойств у аморфных материа­лов. В кристалле оптическая и электронная энергетические щели равны.

В аморфном материале электронные свойства описываются щелью подвиж­ности, а оптические свойства связаны с оптической щелью, которая обычно меньше щели подвижности приблизительно на 50-100 мэВ [35].