ТОНКОПЛЕНОЧНЫЕ. СОЛНЕЧНЫЕ ЭЛЕМЕНТЫ. НА ОСНОВЕ КРЕМНИЯ
Факторы, определяющие КПД солнечного элемента
Предельный термодинамический КПД идеального преобразователя солнечной энергии определяется как
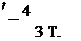
![]() Лпред ~
Лпред ~
V " " с J
где Т — температура приемника; Тс — температура источника.
Спектр излучения Солнца может быть аппроксимирован спектром излучения абсолютно черного тела, нагретого Тс = 5800 К. Тогда для температуры приемника Т ~ 300 К можно получить Рпред — 93 ^% [17].
Определение предельного теоретического КПД, исходя из наиболее общих принципов, представлено в работе [19]. Расчеты сделаны на основе принципа детального равновесия при рассмотрении потоков излучения в системе, состоящей из Солнца, которое считается абсолютно черным телом, и солнечного элемента. Для условия отсутствия концентрирования сол
нечного света авторы определили предельный теоретический КПД = 30 % при оптимальной ширине запрещенной зоны полупроводника 1,1 эВ, что близко к ширине запрещенной зоны Si.
В работе [20] для единичного солнечного элемента и теоретически максимального коэффициента концентрации солнечного излучения С = 46 200 (определяется как отношение излучаемой с единицы поверхности Солнца мощности к плотности мощности солнечного излучения в окрестностях Земли [17]) был получен предельный КПД = 40 %. Для неограниченного количества элементов в каскадной структуре предельный КПД = 68 % при С = 1 и КПД = 87 % при С = 4,6-104 [21].
 |
Однако солнечный фотоэлемент преобразует только часть падающей
![]() Электрическая энергия
Электрическая энергия
Рис. 2.9. Потери энергии в солнечном элементе: Rш — шунтирующее
сопротивление; Rп — последовательное сопротивление
Анализ распределения потерь энергии падающего излучения в кремниевом солнечном элементе (КПД = 16,6 %, ff = 0,78) при работе в условиях AM 1,5 проведен в работе [21]:
• термализация (передача энергии решетке) горячих носителей заряда, возникающих при поглощении фотонов с энергией hv > Eg — 29,2 %;
• прохождение через элемент фотонов низких энергий hv < Eg, не сопровождающееся генерацией электронно-дырочных пар — 18,8 %;
• неполное собирание фотогенерированных носителей заряда — 4,5 %;
• рекомбинационные потери носителей заряда в переходе, определяемые диодными параметрами — 19,2 %;
• потери мощности в диоде при прямом напряжении смещения, равном Vm, омические потери мощности I2R на последовательном и шунтирующем сопротивлениях — 4,7 %;
• потери на отражение (отражение света от фотоприемных поверхностей) — 2,0 %;
• потери на затенение поверхности контактной сеткой — 4,0 %;
• нефотоактивное поглощение (поглощение света просветляющим покрытием, дефектами и т. д.) — 1,0 %.
Из перечисленного видно, что наибольшими в СЭ являются потери на термализацию горячих носителей заряда.
Проникновение излучения через поверхность фотоэлемента. Первым явлением, вызывающим потерю падающей энергии, является отражение излучения от поверхности полупроводника. Отражение в значительной мере определяется состоянием поверхности, а также зависит от физических параметров полупроводника. В соответствии с расчетами для материалов со структурой алмаза и шириной запрещенной зоны 1,0—1,5 эВ следует ожидать отражения около 30 %. Для кремния отражение в видимой области спектра составляет около 40 %. Чтобы уменьшить потери, вызванные отражением, на поверхности кремния создается просветляющий слой, например из SiO2.
КПД проникновения, показывающий, какая часть падающей энергии проникает через поверхность полупроводника в глубь пластинки, определяется из выражения
! Ex(1 - Rx)dX
^пр = ^------------------- , (2.24)
! Exd x
0
где Rx — отражение; Ex d X — часть энергии падающего излучения в промежутке длин волн от X до X + dX.
Поглощение излучения. Часть излучения, проникающего в глубь полупроводника, поглощается в нем. Остальная часть излучения проходит через
всю толщину пластины и бесполезно поглощается задним металлическим электродом. КПД поглощения излучения в полупроводнике находится из выражения
![]()
![]() I ek(1 - R0P-exp(-a®)] dк 0________
I ek(1 - R0P-exp(-a®)] dк 0________
да
I Ek(1 - Rk) dk
0
где a — коэффициент поглощения; ® — толщина пластины.
Количество энергии, теряемой в результате поглощения задним электродом, определяется коэффициентом поглощения излучения и толщиной полупроводниковой пластинки, в которой выполнен ^-«-переход. Обычно до заднего электрода доходит очень малая часть излучения в длинноволновой части спектра.
Генерация носителей заряда. Не вся поглощенная в объеме полупроводника энергия идет на генерацию пар электрон-дырка. Часть ее тратится на образование экситонов и возбуждение колебаний кристаллической решетки, что приводит к повышению температуры полупроводника. Поглощение, связанное с генерацией пар электрон-дырка, определяется квантовым выходом внутреннего фотоэффекта Цк.
КПД генерации, определяющий ту часть поглощенной полупроводником энергии, которая вызывает образование пар электрон-дырка, находится по формуле
ко S
I ЦкEk(1 - Rk)[1 - exP(-a®)] dк Цг = -°5------ . (2.26)
I Ek(1 - Rk)[1 - ЄХР (-a®)] dк о
Край собственного поглощения определяет длинноволновую границу ко5 спектральной характеристики прибора. Так как для к > ко5 имеем Цк = 0, то верхний предел интегрирования в числителе ограничивается ко5. Это свидетельствует о том, что для данного спектра излучения КПД генерации цг является функцией ширины запрещенной зоны Eg.
На рис. 2.1о представлен спектр солнечного излучения и кривые, определяющие максимальную величину энергии с данной длиной волны, которая может идти на генерацию пар электрон-дырка в полупроводниках с
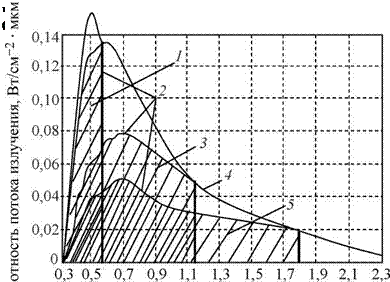 |
разной шириной запрещенной зоны. Приведенные кривые рассчитаны для случая, не учитывающего отражение от поверхности и проникновение излучения до заднего электрода, т. е. R ^ = 0 и ю = да.
Рис. 2.10. Спектр солнечного излучения и кривые,
определяющие величину энергии излучения с длиной волны,
используемой для генерации пар электрон-дырка в различных
полупроводниках: 1 — Eg = 2,5 эВ [GaP], 5,8-1016 пар/с;
2 — энергия для генерации пар электрон-дырка в полупроводнике
с шириной запрещенной зоны Eg; 3 — Eg = 1,1 эВ [Si], 2,8-1017 пар/с;
4 — спектр солнечного излучения; 5 — Eg = 0,68 эВ [Ge], 4,2-1017 пар/с
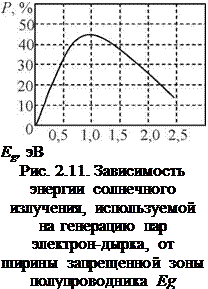
Как видим, энергия длинноволновой части спектра, соответствующая энергии квантов, меньшей чем Eg полупроводника, полностью теряется. В связи с этим количество полезно поглощенных фотонов уменьшается при увеличении Eg полупроводника. Однако с увеличением ширины запрещенной зоны относительно возрастает поглощение в области максимума солнечного спектра, где фотоны имеют более высокую энергию. Поэтому существует оптимальная ширина запрещенной зоны, при которой часть энергии спектра, идущая на генерацию пар электрон-дырка, наибольшая (рис. 2.11).
Рекомбинация и ток. В прохождении электрического тока во внешней цепи принимают участие те пары электрон-дырка из общего количества образованных в объеме полупроводника, которые генерируются на расстоянии от перехода, не большем диффузионной длины. Остальные пары, которые рекомбинируют перед их разделением потенциальным барьером, определяют токовые потери. КПД фотоэлемента по току вычисляется по формуле
^0 s
J £>хЛхEx(1 - Rx)^ - exP(-аю)] dX Лі = -^ , (2.27)
J ЛхEx(1 - Rx)[1 - exP(-аю)] dx 0
где Qx — коэффициент разделения носителей.
 Рекомбинация и напряжение. Как уже отмечалось, фотоны с энергией, значительно превышающей ширину запрещенной зоны полупроводника, образуют пары электрон-дырка, энергия которых в момент образования намного больше средней энергии равновесных носителей заряда. Однако избыток энергии быстро теряется в результате соударения с атомами решетки, поэтому энергия образованных носителей почти сразу приближается к средней энергии равновесных носителей в зонах (процесс термализации горячих носителей). Потеря энергии носителей при переходах внутри зоны вызывает потерю напряжения в солнечном фотоэлементе.
Рекомбинация и напряжение. Как уже отмечалось, фотоны с энергией, значительно превышающей ширину запрещенной зоны полупроводника, образуют пары электрон-дырка, энергия которых в момент образования намного больше средней энергии равновесных носителей заряда. Однако избыток энергии быстро теряется в результате соударения с атомами решетки, поэтому энергия образованных носителей почти сразу приближается к средней энергии равновесных носителей в зонах (процесс термализации горячих носителей). Потеря энергии носителей при переходах внутри зоны вызывает потерю напряжения в солнечном фотоэлементе.
Потеря напряжения, обусловленная переходом одного электрона, определяется отношением
еЕф = еЕфХ hv hc
где Eф — фотоЭДС, вырабатываемая электроном на контактах элемента,
hv — поглощенная электроном энергия в момент генерации в зоне.
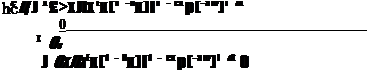 |
||
КПД по напряжению для всех действующих фотонов определяется по формуле
В выражении (2.28) не учитываются потери напряжения, обусловленные его падением на последовательном сопротивлении ^-«-перехода.
Умножая значение КПД отдельных процессов, определяемых в выражениях (2.24)-(2.28), находим результирующую эффективность
ЄЕф I hQX^XEx(1 - Rx)[1 - exP(-а®)] dE
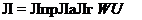 nc 0_________________________________________
nc 0_________________________________________
IE, d E 0
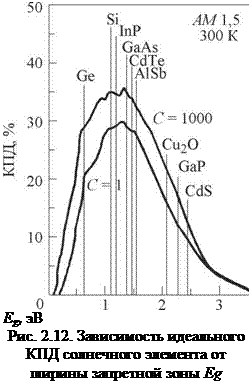
Выбор оптимального полупроводника. На рис. 2.12 приведена зависимость идеальной эффективности солнечного элемента при 300 К от ширины запрещенной зоны. Одна кривая соответствует обычному излучению (C = 1), а другая — х1000 концентрированного солнечного излучения (C = 1000). Небольшие осцилляции на ней связаны с характером поглощения излучения в атмосфере. Видно, что кривая эффективности имеет широкий максимум, в пределах которого КПД слабо зависит от Eg. Поэтому все полупроводники, которые имеют ширину запрещенной зоны от 1 до 2 эВ, относятся к материалам, пригодным для создания солнечных элементов. Существует ряд факторов, снижающих идеальную эффективность, вследствие чего реальные значения эффективности преобразования ниже идеальных.
![]()
 % %
% %
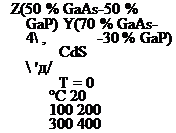 28
28
24
20
16
12
8
4
0
0,2 0,6 1,0 1,4 1,8 2,2 2,4 2,6 2,8 3,0
Eg, эВ
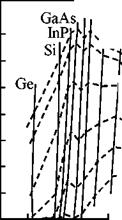
Рис. 2.13. Зависимости теоретического КПД
идеального солнечного элемента
с гомопереходом от ширины запрещенной
зоны полупроводника
Соотношение между теоретическим КПД солнечных элементов с гомопереходом и шириной запрещенной зоны полупроводника в условиях АМ 0 при различных температурах представлено на рис. 2.13 в отсутствии рекомбинационных потерь носителей заряда на поверхности. Максимум
кривых расположен вблизи энергий 1,4—1,5 эВ. При повышенных температурах максимумы смещаются в область больших значений ширины запрещенной зоны [21].
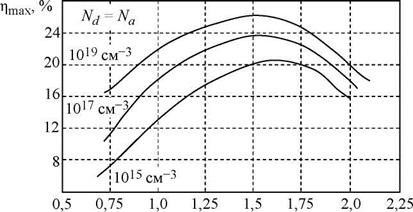
На рис. 2.14 представлена зависимость максимального КПД солнечного фотоэлемента от ширины запрещенной зоны полупроводника для трех значений концентраций доноров и акцепторов. Кривые получены в результате расчетов, выполненных для германия Eg = 0,7 эВ, кремния Eg = 1,1 эВ, ан - тимонида индия Eg = 1,6 эВ и гипотетического полупроводника Eg = 2,0 эВ аппроксимацией спектра солнечного излучения спектром излучения абсолютно черного тела с температурой T = 5760 К и интегральной излучательной способностью 0,1 Вт/см2. Потери на отражение и во внутренних сопротивлениях фотоэлемента не учтены.
|
|
Eg, эВ
Рис. 2.14. Зависимость максимального КПД солнечного элемента от ширины запрещенной зоны полупроводника
КПД фотоэлемента увеличивается по мере повышения концентрации примесей. Это связано с тем, что при увеличении концентрации примесей уровень Ферми в обеих областях p-n-перехода перемещается в направлении границ запрещенной зоны, благодаря чему увеличивается высота потенциального барьера в переходе. Оптимальный полупроводник для преобразования солнечной энергии должен иметь ширину запрещенной зоны около 1,6 эВ (см. рис. 2.14).
В действительности распределение солнечной энергии на Земле далеко от идеального и связано с тремя основными источниками атмосферного поглощения, а именно: газами (O2, N2 и др.), водяным паром и пылью. В результате атмосферного поглощения ослабляется ультрафиолетовая часть солнечного
спектра. Влияние названных источников поглощения можно описать, если ввести длину оптического пути (воздушная масса AM) и количество водяного пара в атмосфере w. Поглощение будет тем больше, чем больше AM и w.
С учетом изменения солнечного спектра под влиянием географических и атмосферных условий поток фотонов Q(Eg), способных генерировать пары электрон-дырка в полупроводнике с шириной запрещенной зоны Eg, определяется как
![]() Q (Eg )= s Q M >
Q (Eg )= s Q M >
Eg h
![]() где Q(v) — поток фотонов с энергией hv на отрезке А — = 10 5 •см_1;
где Q(v) — поток фотонов с энергией hv на отрезке А — = 10 5 •см_1;
vmax — максимальная частота в спектре солнечного излучения.
Зависимость потока фотонов Q(Eg) и плотности тока, которые образовали бы генерированные этими фотонами пары при их полном разделении, представлена на рис. 2.15. Поглощение в атмосфере приводит к уменьшению плотности тока и количества фотонов в полупроводнике. Соответствующие изменения наблюдаются в зависимости от максимальной теорети-
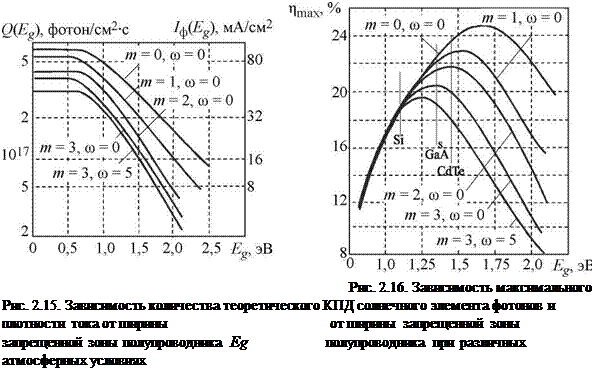 |
ческой величины КПД солнечного элемента и от ширины запрещенной зоны полупроводника (рис. 2.16).
Чем сильнее поглощается излучение атмосферой, тем при более низком значении Eg достигается оптимальная величина Лтах(см. рис. 2.16). С другой стороны, для полупроводников с меньшим значением Eg влияние
атмосферы проявляется слабее, а характеристики солнечных элементов на их основе становятся сопоставимыми с характеристиками солнечных элементов на основе более широкозонных материалов.
ФотоЭДС солнечного элемента при комнатной температуре определяется как
Для достаточно больших интенсивностей излучения, при которых
1ф >> Is, единица в формуле (2.29) может быть опущена.
Если рассматривать ^-«-переход, в котором концентрация примесей в диффузионном слое p-типа значительно больше, чем в исходной пластине «-типа, (что имеет место в солнечных элементах), то плотность тока насыщения определяется уравнением
1
![]()
![]() 2
2
Lh 1h
где p« — равновесная концентрация дырок в «-области; Dh, Lh, ih — соответственно коэффициент диффузии, диффузионная длина и время жизни дырок. Подставляя известные выражения
1
![]() «n =-------- ,
«n =-------- ,
е^ер« где ре, р« — подвижность электронов и удельное сопротивление материа
 |
ла, для фотоЭДС солнечного элемента из кремния с базой перехода «-типа при температуре 300 К находим
Если на лицевую поверхность солнечного элемента (см. рис. 2.2) падает монохроматический свет с длиной волны X и энергией фотонов hv > Eg, зависимость скорости генерации электронно-дырочных пар от расстояния х от поверхности полупроводника определяется выражением [12]
G(X, x) = a(X)F(X)[1 - R(X)]exp[- a(X)x], (2.31)
где a(X) — коэффициент поглощения; F(X) — плотность потока падающих фотонов в единичном спектральном интервале; R (X) — доля фотонов, отражающихся от поверхности.
Генерируемый светом в солнечной батарее фототок может быть найден из уравнения непрерывности для избыточных носителей. При низком уровне инжекции одномерное стационарное уравнение непрерывности для дырок в полупроводнике и-типа имеет вид
Gp _ Рп _ Рп° _ IJ = 0. (2.32)
F Xp e dx
Уравнение непрерывности для электронов в полупроводнике p-типа
п p — п Р0 1 dJ
Gn —p------ Р0 —1 dJn = 0. (2.33)
хп e dx
Отсюда плотность тока дырок и электронов определяется выражениями
|
Jp ePppnE eDp dx, |
(2.34) |
|
dnp |
|
|
Jn = ePnnpE ^ eDn d ' (AJv |
(2.35) |
В этих выражениях Jp и Jn — плотность дырочного и электронного токов. В солнечном элементе с резким p-n-переходом и постоянными уровнями легирования по обеим сторонам перехода (рис. 2.17) электрическое поле вне обедненной области отсутствует. Из выражений (2.31), (2.32), (2.34) можно получить уравнение, описывающее распределение неосновных носителей дырок в и-области
Dp—pn _ pn—pn0 + aF (1 — R)exp(-ax) = 0. (2.36)
dx X p
Общее решение этого уравнения имеет вид
pn - pn0 = Ach(x/Lp) + Bsh(x/Lp) - Cexp(- ax) , где Lp = (DpXp)1/2 — диффузионная длина; A, B, C — константы.
34
Использование в уравнении (2.36) частного решения pn - pno = C exp(- ax) позволяет определить C:
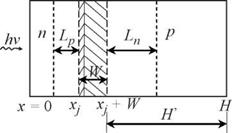 C = aF(1 - R)tp / (a2Lp -1).
C = aF(1 - R)tp / (a2Lp -1).
Константы A и B определяются в реРис. 2.17. Размеры солнечного
зультате использования граничных условий элемента и характерные длины на фронтальной поверхности (при x = 0), даффузии не°сн°вных шоттелет где происходит рекомбинация, и на границе обедненной области. Первое условие может быть получено, если учесть, что при x = 0 плотность диффузионного тока равна плотности поверхностного рекомбинационного тока
DP d(Vn0) = SP(Pn - Pn0),
где Sp — скорость поверхностной рекомбинации.
Второе граничное условие справедливо для границы области пространственного заряда, где избыточная концентрация неосновных носителей мала, что связано с их удалением полем из области обеднения. Таким образом,
Pn - Pn0 = 0 при x = Xj.
Подстановка этих граничных условий в уравнение (2.36) позволяет получить выражение для избыточной концентрации дырок:
Pn - Pn0 = [aF(1 - R)V(a2LP2 - 1)] (SpLp / Dp +aLP ) х
—ax ■
sh[(xj - x) / Lp ] + e j [(SpLp / Dp)sh(x / Lp) + ch(x / Lp)] - ax
(SpLp / Dp)sh(xj / Lp) + ch(xj / Lp)
Тогда плотность дырочного фототока, генерируемая фотонами с длиной волны X, на краю обедненной области равна
элемента с р-базой при заданной длине волны падающего излучения и предполагая, что время жизни носителей, их подвижность и уровень легирования в этой области постоянны.
Чтобы найти электронный фототок, собираемый из подложки, необходимо использовать уравнения (2.31), (2.33) и (2.35) при следующих граничных условиях:
np - Про = 0 при x = Xj + W, (2.39)
где H — полная толщина солнечного элемента; W — ширина обедненной области.
Условие в выражении (2.39) означает, что избыточная концентрация неосновных носителей вблизи края обедненного слоя равна нулю, а в (2.38) — определяет скорость поверхностной рекомбинации вблизи омического контакта на тыловой поверхности.
Использование этих граничных условий позволяет определить плотность электронного фототока, генерируемого фотонами с длиной волны X, на краю обедненной области р-базы (x = Xj + W):
где Hi — толщина квазинейтральной области р-базы.
В дополнение к диффузионным составляющим фототока, собираемым в квазинейтральных n - и p-областях (уравнения (2.37) и (2.40) соответственно), необходимо учесть дрейфовую компоненту, возникающую в области обеднения. Электронно-дырочные пары, генерируемые светом в области обеднения, выносятся из этой области электрическим полем еще до того, как успевают рекомбинировать между собой. Поэтому фототок обедненного слоя в единичном спектральном интервале равен числу фотонов, поглощаемых в этом слое в единицу времени:
Jdr = eF(1 - R)exp(- axj)[1 - exp(- aW)]. (2.41)
Таким образом, фототок, генерируемый в солнечном элементе светом с длиной волны X, определяется суммой выражений (2.37), (2.40) и (2.41)
Jl(X) = Jp(X) + Jn(X) + Jdr(X). (2.42)
Полная плотность фототока, протекающего при освещении элемента на основе p-n-перехода солнечным светом со спектральным распределением F(X), можно получить интегрируя выражение (2.42):
X2
Jф = I [Jp (X) +Jn (X) + Jdr (X)]dX,
X1
где X1 и X2 — коротковолновая и длинноволновая границы поглощения.
Для типичного солнечного элемента на основе p-n-перехода X1 = 0,3 мкм. Красная граница поглощения определяется шириной запрещенной зоны полупроводника. Связь между длиной волны красной границы поглощения Xqs, мк, и шириной запрещенной зоны полупроводника Eg, эВ, описывается
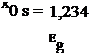 |
уравнением
Для кремния (Eg = 1,12 эВ при T = 300 К) красная граница поглощения находится вблизи 1,1 мкм.
Выражение (2.42) позволяет рассчитать спектральный отклик солнечного фотоэлемента. Спектральным откликом называется число собираемых электронов, приходящихся на один падающий фотон при данной длине волны.
Спектральный отклик SP равен фототоку Jl(X) (выражение (2.42)), деленному на величину eF, при наблюдаемом (внешнем) отклике, либо деленному на величину eF (1 - R), при внутреннем спектральном отклике
J p (X) + Jn (X) + Jdr (X)
SR = -^---------- ^-------- d^-L. (2.43)
eF (X)[1 - R(X)]
Если спектральный отклик известен, полная плотность фототока, протекающего при облучении элемента солнечным светом со спектральным распределением F(X), равна
X 2
JL = e j F(X)[1 - R(X)]SR(X)dX.
XI
Коротковолновый край спектральной зависимости Q(X) определяется в основном сбором носителей из фронтального слоя, а длинноволновый край — из базовой области.
В СЭ на основе непрямозонных полупроводников значительная часть излучения с hv > Eg генерирует электронно-дырочные пары глубоко в базовой области, что обусловливает пологую спектральную зависимость Q в длинноволновом участке спектра фотоответа вследствие рекомбинации части генерированных носителей в объеме базы и на тыльной поверхности.
В СЭ на основе прямозонных полупроводников благодаря более резкому краю поглощения значения Q имеют более резкий подъем в длинноволновой части спектра. Однако «поверхностное» поглощение в этом случае начинается при больших значениях X, что приводит к более быстрому спаду значений Q при уменьшении X, из-за рекомбинации фотогенериро - ванных носителей на фронтальной поверхности [17].
Реальный внутренний спектральный отклик для кремниевого солнечного элемента с p-базой существенно отличается от идеальной ступеньки (рис. 2.18 [12]). При расчетах использовались следующие параметры прибора: Nd = 5-1019 см-3, Na = 1,5-1016 см-3, ip = 0,4 мкс, in = 10 мкс, Xj = 0,5 мкм, H = 450 мкм, Sp (лицевая поверхность) = 104 см/с, Sn (тыльная поверхность) = да. На рис. 2.18 приведены также спектральные зависимости вклада каждой из трех компонент тока. При поглощении фотонов с низкими энергиями основная доля носителей генерируется в базовой области, поскольку коэффициент поглощения в Si при этом мал. Если же энергия фотонов превышает 2,5 эВ, основной вклад в фототок вносит лицевой слой. При энергиях фотонов выше 3,5 эВ а превышает 106 см-1 и спектральный отклик полностью определяется лицевым слоем. Поскольку величина Sp предполагается достаточно большой, поверхностная рекомбинация на лицевой поверхности элемента приводит к значительному уменьшению спектрального отклика по сравнению с идеальным значением. При aLp >> 1 и axj >> 1 спектральный отклик приближается асимптотически к величине, которая определяется фототоком лицевой стороны перехода, равной
![]() 1 + S p/aDp
1 + S p/aDp
SR =---------------------- p------- p----------------
(SpLp / Dp)sh(Xj / Lp) + ch(Xj / Lp)
Скорость поверхностной рекомбинации Sp сильно влияет на спектральный отклик, особенно при высоких энергиях фотонов. На рис. 2.19 приведены кривые спектрального отклика, рассчитанные для прибора с теми же параметрами (см. рис. 2.18). При этом скорость Sp изменялась в диапазоне
102...106 см/с. Наблюдается сильное уменьшение спектрального отклика при увеличении Sp. Из выражения (2.44) следует, что при заданной величине Sp спектральный отклик улучшается при увеличении диффузионной длины Lp. В общем случае для роста спектрального отклика в диапазоне используемых длин волн следует уменьшать Sn и Sp и увеличивать Ln и Lp.
|
1,0 |
1 |
Полный |
|
и 0,8 |
. 1 Идеаль ный | "отклик |
^■''■''отклик |
|
0,6 |
Базо- Лицевой |
|
|
А 0,4 сЗ Он |
: |
вая об - слой |
|
1 II |
ласть Обедненный |
|
|
Спект о КЗ |
||
|
слой |
|
0 1 2 3 4 5 |
|
hv, эВ |
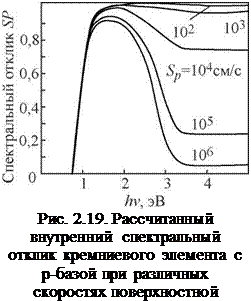 Рис.2.18. Рассчитанный внутренний
Рис.2.18. Рассчитанный внутренний
спектральный отклик кремниевого
элемента с р-базой
Итак, наблюдается резкое падение коэффициента собирания в коротковолновой области, вызванное плохими диффузионными и рекомбинационными параметрами легированного слоя, определяется неполным собиранием носителей из базы [18].
Увеличить Q можно за счет уменьшения поверхностной рекомбинации. Это достигается тщательной обработкой поверхности полупроводника с целью устранения рекомбинационных центров. Кроме того, эффективная скорость поверхностной рекомбинации зависит от наличия потенциального барьера, что также дает принципиальную возможность снижения рекомбинации.
В арсениде галлия скорость поверхностной рекомбинации значительно выше, чем в кремнии. Выращивание на поверхности GaAs тонкого широкозонного слоя из твердого раствора AlxGa1-xAs (x = 0,75-0,9) позволяет существенно снизить скорость поверхностной рекомбинации на гетерогранице благодаря близости периодов решеток GaAs и AlAs и меньшему числу оборванных валентных связей на гетерогранице, чем на свободной поверхности GaAs [22]. Потенциальный барьер на гетерогранице препятствует попаданию носителей тока, генерированных в узкозонном материале, на поверхность широкозонного слоя. В этом случае величина коэффициента
собирания в коротковолновой области определяется спектральной зависимостью показателя поглощения широкозонного слоя твердого раствора. При малых толщинах этого слоя (< 0,1 мкм) возможно сохранение высокой фоточувствительности и для самого коротковолнового участка солнечного спектра (при X < 0,4 мкм).
Второй путь повышения Q связан с уменьшением толщины лицевого легированного слоя для того, чтобы сделать неэффективный легированный слой более прозрачным для фотонов солнечного спектра [18]. Однако создание мелких переходов ограничивается возрастанием сопротивления растекания токов. Кроме того, в тонких легированных слоях резко возрастает влияние рекомбинации на внешней поверхности. Для мелких переходов существует проблема создания металлических контактов, обусловленная возникновением объемных шунтов, которая также ограничивает уменьшение толщины слоя. Все это создает некоторую оптимальную толщину поверхностного легированного слоя.
Третий путь направлен на повышение чистоты полупроводникового слоя, что резко уменьшит объемную безызлучательную рекомбинацию. Потребуются необходимые разработки технологии получения высококачественных исходных материалов и приборов, которые не ухудшали бы исходные параметры. В настоящее время значительное ухудшение параметров базы возникает в результате термообработки элементов. Кроме того, большое количество рекомбинационных дефектов возникает при создании ^-и-перехода за счет введения посторонних примесей.
Наконец, четвертый путь повышения эффективности собирания носителей связан с созданием в слоях фотопреобразователя встроенных электрических полей, способствующих дрейфу неосновных носителей к р-п-переходу.