ТЕХНОЛОГИЯ КАТАЛИЗАТОРОВ

ПОРИСТАЯ СТРУКТУРА КАТАЛИЗАТОРОВ

При создании катализаторов необходимо предусмотреть их максимальную производительность, селективность и устойчивость в работе. Только созданием определенного химического состава эти показатели не обеспечить. Таким образом, на современном этапе научные основы приготовления катализаторов включают формирование оптимальной пористой структуры. В последние годы с использованием уже известных активных химических соеди­нений, в основном вследствие совершенствования структуры, по­лучены новые более эффективные контактные массы [40, 51, 61 ].

Пористая структура катализатора характеризуется главным образом радиусом пор г, их объемом v и площадью поверхности S. Согласно строению и физико-химическим свойствам пористые тела принято делить на два основных класса: губчатые и корпускулярные (ксерогели) [51, 55, 62, 63]. Твердые тела губчатой структуры пронизаны конусными, цилинд­рическими и бутылкообразными порами.

В корпускулярных (глобулярных) структурах поры образо­ваны промежутками между касающимися частицами (корпуску­лами, глобулами), составляющими основу, скелет материала [51, 63]. Существуют смешанные структуры, в которых комбинируются оба вида пор [51 ]. Примерами катализаторов раз­личного типа могут служить: алюмосиликатные катализаторы крекинга (корпускулярные); пористые стекла, некоторые угли (губчатые); никелевые катализаторы, имеющие корпускулярную структуру из частиц никеля, которые в свою очередь пронизаны цилиндрическими, бутылкообразными порами, сформировавши­мися при удалении порообразователя (смешанная структура).

Глинистые материалы, которые достаточно широко исполь­зуют в катализе, имеют пластинчатую (слоистую) структуру. Они состоят из пластинок, ширина которых много больше толщины. Поры имеют щелевидную и клиновидную форму [55, 64]. Волокнистые материалы типа ас­беста также находят применение при создании катализаторов (а. с. СССР 929211). Особняком стоят цеолиты и ряд других микропористых материалов [65]..

Из всех перечисленных структур наиболее распространенной является корпускулярная (глобулярная) [51 ], в которой опреде­ляющими являются два параметра: размер глобул и плотность их упаковки. Изменения этих параметров во многом определяют разнообразие пористых структур. Характеристики пористого тела (удельная площадь поверхности, объем и размер пор), а также различные свойства (адсорбционные, диффузионные, механиче­ские, капиллярные и другие) являются функцией этих двух пара­метров.

Для удобства расчета геометрии глобулярных структур сделано допущение об их монодисперсности. В таком случае размер гло­бул монодисперсной глобулярной модели возможно получить из удельной площади поверхности или как среднее эксперимен­тальное значение с помощью микроскопа.

Плотность упаковки численно может быть выражена пори­стостью фсв, т. е. долей объема пористого тела, приходящегося на поры (относительный свободный объем, см3/см3):

= + (2-7)

А размер глобул модели вычислен из удельной площади поверх­ности (5уд, м2/г) образца:

D = 6-10s/(p„CTSra). (2.8)

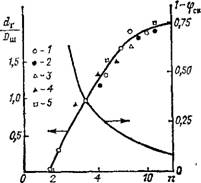
Рис. 2.4. Интерполяционные кривые зави­симости степени заполнения (1 — Фсв) и относительного размера горла пор <<г//>ш от числа контактов п для упаковок шаров:

1 — точки для выбранных правильных упаковок шаров; 2— 5 — эксперименталь­ные точкн по результатам разных работ для случайных упаковок шаров; dr — диа­метр горла пор; £>ш — диаметр шара

Здесь V и vr — объем пор и гло­бул, которые находят из кажущейся и истинной плотности [51]; D — диа­метр глобул, мм; рист — истинная плотность частиц, г/см3.

Второй параметр модели определяется из пористости фсв; по этой величине можно определить число контактов каждой гло­булы с соседними (п). Для определения п используют зависимость пористости от п (рис. 2.4) [66, 67]. Диаметр полости поры (Da_ п) можно выразить диаметром вписанного в нее шара (Dm), а раз­мер горла (£)г. п) диаметром вписанной в него окружности (D). Ниже приведены характеристики правильных упаковок, шаров [20]:

Число контактов...................... 4 6 8 12

Пористость, %......................... 65,99 47,64 31,98 25,95

К\...................................................... 1,016 0,476 0,246 0,184

K2 .................................................... 0,915 0,414 0,225 0,155

K3 ............................................ 1,00 0,732 0,291 0,225

З

Примечание. fcj = ип - Ош; =Dr_ n - D; = Dn n • Dm (здесь t»n — объем поры на 1 шар).

Число п, равное 12, соответствует плотнейшим упаковкам — гексагональной или кубической гранецентрированной; п = 8 — кубической объемно-центрированной; п = 6 — простой кубиче­ской; n, = 4 — тетраэдрической. В геометрически подобных си­стемах, таким образом, с различным размером глобул пористость и число контактов одной глобулы сохраняются.

В случае монодисперсной однородной модели, если значение внутренней площади поверхности катализатора отнесено не к единице массы (5УД), а к единице объема (5уд), получим [51 ]:

T 5уд = Фсв^ЇгР - (2.9)

Здесь гг — радиус глобулы; р — число глобул в 1 см3 катализатора.

Относительный объем уг, занимаемый глобулами, составляет (1 — Фсв), где свободный объем фсв не зависит от размера сфери­ческих глобул и определяется способом упаковки.

Объем глобул в 1 см3 катализатора, выраженный через раз­мер и число глобул в нем, будет равен:

І - Фсв = (2-Ю)

Внутренняя площадь поверхности 1 см3 катализатора, выра­женная через свободный объем и радиус глобулы, ориентировочно составляет:

_ 4яг»(1-фсв)-3 3(1-Фсв) уД ^ ' (2 }

Таким образом, внутренняя площадь поверхности глобуляр­ного монодисперсного катализатора обратно пропорциональна радиусу (размеру) глобул, т. е. она обратно пропорциональна эквивалентному радиусу пор, которые представляют собой зазоры между глобулами. Следовательно, скорость реакции и в кине­тической области пропорциональна площади поверхности пор и обратно пропорциональна их радиусу:

U^^S, (2.12)

S = a2/r. (2.13)

Здесь ctj и а2 — коэффициенты пропорциональности.

Для перехода на глобулы неправильной формы Г. К - Боресков предлагает ввести выражение для гидравлического радиуса 'гидр (20]. При беспорядочной упаковке глобул оно запишется как отношение свободного объема к внутренней площади поверх­ности 1 см3 катализатора:

_ фсв___________ Фсв^г /о /ль

Rmp~s;a - 3(1-фсв) • <2Л4>

Пористые материалы классифицируются не только по геомет­рии пор, но и по их размерам. Существует ряд классификаций именно по этому признаку [51 ]. Деление, предлагаемое тем или иным автором, является чисто условным. Так, М. М. Дубинин определяет три типа пор: макропоры, для которых нижний предел радиуса кривизны можно принять 100—120 нм (1 ООО—1200 А); переходные поры, у которых эффективный радиус кривизны лежит в пределах от 120 до 1,5 нм и, наконец, микропоры с радиусом менее 1,5 нм [68]. А. В. Киселев основными признаками для от­несения адсорбентов к тому или иному типу структуры считает характеризующие их изотермы адсорбции; всего же выделено четыре типа [69]. И. Е. Неймарк расширяет классификацию Киселева до пяти типов, вводя уточнение в виде подгрупп с их характеристикой [51, 65].

Протекание той или иной реакции на поверхности катализа­тора всегда связано с транспортировкой реагирующих веществ и продуктов реакции к участкам внутренней поверхности и от них. Как указано (см. гл. 1), в зависимости от условий процесса, активности, пористой структуры и размеров зерен катализатора процесс могут лимитировать собственно химические превращения (кинетическая область) либо диффузионные торможения (диффузи­онная область) [39, 51, 70].

Степень уменьшения концентрации реагентов от периферии к центру частицы (зерна) катализатора определяет эффективность использования его внутренней поверхности (или пор). Степень использования внутренней поверхности г], определяемая как от­ношение наблюдаемой скорости реакции к скорости реакции при полном использовании внутренней поверхности, имеет специфи­ческую функциональную зависимость от основных параметров пористости в различных областях протекания реакции. Скорость каталитической реакции, отнесенная к единице объема зерна ка­тализатора «', зависит от скорости реакции иа, отнесенной к еди­нице поверхности катализатора (удельной каталитической актив­ности), от площади поверхности S'yA и ее доступности, которая ха­рактеризуется степенью использования внутренней поверхности т);

= (2.15)

Удельная активность катализатора данного химического со­става приблизительно постоянна, и максимум скорости реакции отвечает максимуму произведения 5уДт]. Пористую структуру, обеспечивающую это условие, считают оптимальной [20, 71 ].

Степень использования внутренней поверхности определяется безразмерным параметром ¥ (модуль Тиле). Этим же параметром удобно количественно оценивать границу областей протекания реакции:

0.5

(2.16)

Здесь L — расстояние от периферии до центра зерна, м; С — концентрация основного компонента у поверхности зерна катализатора, моль/м3; Дэ — в м2/ч; и8 — в моль/(м2-ч).

При ¥ < 0,5 процесс идет в кинетической области и степень использования внутренней поверхности близка к единице. При Y > 2,5 процесс протекает в области внутренней диффузии, ис­пользуется лишь ограниченная приповерхностным слоем зерна часть катализатора. В этой области степень использования внут­ренней поверхности примерно обратно пропорциональна Y, а эффективная глубина /э проникновения реагентов в пористое зерно для реакции п-го порядка выражается соотношением:

T h = VDj{kCn-1). (2.17)

Когда скорость реакции намного превосходит скорость под­вода реагентов, макроскопическая кинетика определяется про­цессами транспорта и не отражает истинной скорости реакции на поверхности, ее зависимости от температуры, концентрации и других параметров.

Внешняя диффузия является лимитирующей стадией процесса лишь в случае очень быстрых реакций, которые полностью проте­кают на внешней поверхности катализатора; тогда применяют не­пористые контактные массы.

Рис. 2.5. Влияние линейной скорости по­тока реагентов на скорость процесса

Области: I — виешиедиффузиониая; II — переходная; III — виутридиффузиониая или кинетическая

Переход внешнедиффузион - ной области во внутридиффу - зионную или кинетическую свя­зан с линейной скоростью w по­даваемых реагентов. На рис. 2.5 показано, как влияет значение w на скорость процесса в каждой из перечисленных областей. Участок АВ соответствует внешнедиффузионной области, участок CD, параллельный оси абсцисс, — внутридиффузионной или кинети­ческой, а далее по мере роста w увеличивается перемешивание, снижается АС и уменьшается и. Наконец после точки Е наступает полное перемешивание.

При выборе наиболее выгодной макроструктуры катализатора, отвечающей максимальной его активности, следует учитывать ха­рактерные особенности каждой области протекания процесса с тем, чтобы достичь высоких скоростей реакции.