ТЕХНОЛОГИЯ КАРБАМИДА

Уравнение кинетики синтеза карбамида в статическом автоклаве

! Все авторы, которые пытались на основе той или иной модели [3] построить кинетическое уравнение процесса синтеза карбамида, не учитывали одно важное обстоятельство: объем жидкой фазы — реакционной зоны системы — в присут­ствии избыточного аммиака может изменяться в процессе реак­ции в несколько раз. Избыточный аммиак не растворяется в жид­ком карбамате, но по мере дегидратации последнего аммиак начинает растворяться в выделившихся воде и жидком карбамиде. Растворенный аммиак сдвигает равновесие реакции в сторону карб­амида и воды, т. е. возрастает глубина дегидратации. Это, в свою очередь, способствует увеличению содержания воды и карбамида, дальнейшему растворению аммиака, сдвигу равновесия и т. д. Кроме этих факторов на скорость процесса растворения амми­ака должны влиять перемешивание смеси, состояние и форма поверхности контакта фаз, интенсивность ее обновления жидко­стью из глубины фазы. Таким образом, здесь тесно переплетены процессы макроскопической и химической кинетики, проявляю­щиеся в сильном изменении объема реакционной зоны во времени.

Эти представления были положены в основу кинетической мо­дели реакции. Принято, что процесс синтеза обратим, а его кине­тика определяется одновременным протеканием реакций 1, 2, 3 (табл. 1.1) [23]. Стадийность реакции дегидратации при состав­лении кинетического уравнения можно не учитывать, так как в реальном синтезе цианат аммония, видимо, присутствует в нич­тожных количествах. Это, разумеется, не означает, что протекание синтеза по стадиям не влияет на кинетику процесса, изменение механизма обязательно будет отражаться при обработке экспери­ментальных данных на изменении энергии активации и стериче - ского фактора в различных температурных интервалах.

Ограничение реакцией 3 является удобной формализацией: при высоких температурах реакция 3 должна трактоваться как сумма стадий 4 и 5, а при относительно низких температурах — как независимая от стадий доминирующая реакция прямого от­щепления воды от молекул (или ионов) карбамата аммония.

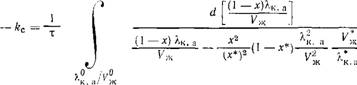
Полагается, что реакция 1 — наиболее быстрая, реакция 2 про­текает с меньшей скоростью, а реакция 3 — наиболее медленная. Процесс синтеза в прямом направлении имеет первый, а в обрат­ном — второй порядок, причем концентрации зависят от времени не только вследствие изменения молекулярного состава смеси, но и изменения во времени степени конденсации NH3, С02 в карб - амат а и объема жидкой фазы Уж. Итоговое кинетическое урав­нение имеет следующий вид [23]:

Va*1-*)/17;

Где индекс «О» относится к т = 0, а * — к состоянию равновесия; kc — константа скорости синтеза карбамида.

Для вычисления kc по уравнению (1.50) необходимо знать зависимости А, к.а = Д (т) и = /2 (т), которые в отличие от х = = /з (т) [21, 24] не поддаются экспериментальному определению в условиях высоких давлений при перемешивании фаз. Име­ются, однако, достоверные зависимости Р — /4 (т) [24], отража­ющие изменение А. к. а, ViK во времени. Чтобы раскрыть эту связь, протекание процесса синтеза во времени представили в виде цепи последовательно расположенных псевдоравновесий: I — когда в начальный период завершается равновесие 1 (см. табл. 1.1), но равновесия 2 и 3 заторможены; псевдоравновесия II — когда завершаются равновесия 1 и 2, но 3 по-прежнему заторможено, и состояния равновесия — когда наступает равновесие всех трех процессов 1, 2 и 3 [23].

Полезность такого подхода заключается в том, что удается избежать математических трудностей, возникающих при описа­нии одновременного сдвига равновесий 1, 2, 3. Для псевдо­равновесий I и II составлены системы трансцендентных уравне­ний, включающие константы равновесий, балансы масс и объемов сосуществующих фаз и уравнения связи давления и мольных объемов компонентов в газе на основе уравнений Битти—Бридж- мена и Мартина—Хао. Летучести компонентов вычислялись по табличным Р—V—Т данным с применением строгих уравнений летучести [25].

Решением систем уравнений на ЭВМ [23] получена связь

Pv Ак. аі1-рп; Уж,-Я,;

В интервале 433—473 К при рсм = 750 кг/м3, L = 4, W = 0. Зависимости а — Р*, Уж — Р* определены из обобщенных уравнений для х*, ср*, 5со2 • Сравнением Р1 [23] и эксперименталь­ных значений Р° при т — > 0 [24] показана их удовлетворительная 40
сходимость. Это означает, что псевдоравновесие I близко реали­зуется на опыте. Псевдоравновесие II, если его рассматривать изолированно от реакции 3 (см. табл. 1.1), не может быть реализо­вано на опыте, поскольку газообразный NH3 не растворяется в жидком карбамате аммония, а лишь способен образовывать при взаимодействии с С02 молекулы карбамата в стехиометрическом количестве. Однако условие заторможенности реакции 3 не озна­чает, что она вовсе не проходит при завершении псевдоравнове­сия II, так как константы равновесия 2 получены в опытах с обя­зательным присутствием в системе карбамида и воды, количества которых определяются стехиометрией реакции 3, но остаются неизменными при соблюдении условий ее заторможенности [13, 19].

В состоянии I можно считать, что реакция 3 не успела пройти сколько-нибудь глубоко (хі —» 0). Это обусловливает спонтанное торможение реакции 2. Однако в состоянии II хи >> 0, что обу­словливает возможность протекания реакции 2. С точки зрения правила фаз Гиббса в состояниях I и II системы аммиак —«кар­бамат» неразличимы, физическое различие заключается в том, что компонент «карбамат» в состоянии I представляет собой ин­дивидуальное расплавленное вещество, а в состоянии II — термо­динамический компонент с постоянным мольным отношением карбамида, воды и карбамата аммония. Это даетдвозможность полагать, что по-прежнему имеет место система аммиак — «карб­амат» с различной степенью заторможенности последнего в каж­дой точке «пути» Р1—>Ри\ А,„.а1 — А, в.аіі; Х1 * Хц-

Аналогично и на пути Рп --> Р*\ хи —> х* эта система существует вплоть до состояния истинного равновесия, в котором затормо­женность реакции 3 определяется закреплением параметров со­стояния Р, Т, L (W — 0). По отношению к этому состоянию система на пути Р1 —* Р*, х{ —» х* неравновесна и не совершает максимальной работы. Но благодаря заторможенности реакции 3 и более высокой скорости реакции 2 в каждой точке этого пути система может рассматриваться как псевдоравновесная система с различным содержанием карбамида и воды в компоненте «карба­мат», обладающая дополнительной степенью свободы. Последняя в замкнутом пространстве при закрепленных L, Т реализуется спонтанным изменением Р на пути I —> II —> *, вызывающимся изменением величин А, к. а, V, K. Отсюда следует, что расчетные за­висимости А, к.а — Р, Vm — Р псевдоравновесной системы и экс­периментальные значения Р — т можно совместить при каждой заданной Т и постоянных L, рсм.

- Абсолютная скорость протекания реакции 3 (или скорость изменения химического состава компонента «карбамата») при условии более быстрого протекания реакции 2 теперь уже не имеет существенного значения. При любой скорости изменения состава «карбамата» в каждой точке пути Р] —> Р* устанавливается

Псевдоравновесие реакции 2 и системы аммиак—«карбамат» в целом. Поэтому введение фактора времени т в термодинамическую логику в данном случае корректно.

Совмещая зависимости А, к.а — Р, Уж — Р с эксперименталь­ными Р — т, получили искомые кривые а — т, Уж — т [23]. Интегрированием (1.50) нашли, что kc не зависит от времени, причем уравнение (1.50) правильно воспроизводит опытные дан­ные вплоть до 483 К, тогда как известные в литературе кинетиче­ские уравнения описывают опытные данные при температуре не выше 453 К [3]. Величины kc даны в табл. 1.8. Как видно из таблицы, kc = f (Т, v) [7] и эта зависимость ослабевает с ростом v, а в координатах уравнения Аррениуса можно наблюдать излом кривых. Это подтверждает тесную связь химических и макро­скопических факторов в данном процессе.