ТЕХНОЛОГИЯ КАРБАМИДА

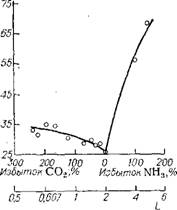
Термодинамика синтеза карбамида

Равновесная степень превращения С0.2. Зависимость величины х* от условий синтеза изучалась многими авторами [51. Большинство работ проведено при L — 2, когда выход карбамида заведомо мал (табл. II.1). Кроме того, известные эксперименталь­ные данные относятся в основном к сравнительно низким t и Р, эти данные значительно расходятся между собой и большинство их не вполне надежно по ряду причин. Между тем на практике предъявляются все более жесткие требования к точности значений х*. Поэтому авторы [5—7] поставили специальные эксперименты по определению значений х* в широком диапазоне параметров процесса на основе усовершенствованной методики исследований. Способ подачи реакционной смеси на синтез с помощью микронасо­сов-дозаторов [8] позволял проводить опыты при любом Р в интер­вале 10—100 МПа; при этом L изменялась от 2 до 6; W — от 0 до 1,6; t — от 170 до 210 °С. Величину х* определяли по анализу жидкой фазы равновесной системы. Средняя квадратичная ошибка экспериментального определения величины х* ох* = 0,56%.

По экспериментальным данным с использованием достоверных литературных сведений методом наименьших квадратов было найдено обобщенное уравнение

Х* = 34,3L — 1.77Z-2 — 29.3Г-І - 3,7LW - j 0,913/ — 0.074Ш — — 5,4 10-в^-(- 0,0234Р—112,1 (II. 1)

Уравнение составлено по результатам 65 опытов; коэффициент множественной корреляции гх* — 0,988; ох* = 2,14%.

Из анализа уравнения (II.1) следует, что кривые зависимости х* — t (при W = const и Р = const) проходят через максимум, причем с увеличением L этот максимум смещается в сторону более низких температур. О существовании самого факта температур­ного кризиса х* было известно давно. Но точная причина этого явления до последнего времени не была установлена. Необходимо отметить, что в большинстве перечисленных в табл. II. I исследо­ваний пофазного отбора проб не производилось и х* вычислялась по валовому составу равновесной смеси. По поводу экстремума зависимости х* — t высказывались [9, 10} предположения о том, что он обусловлен влиянием плотности загрузки автоклава, интенсивным переходом С02 в газовую фазу равновесной системы NH3—С02—СО(МН2)а—Н20 при повышении температуры, а также образованием побочных продуктов (биурета, циануровой кис­лоты). Поскольку уравнение (II. 1) характеризует состав самой жидкой фазы, очевидно, что упомянутые предположения нельзя признать удовлетворительными. Анализ причин температурного кризиса "ж* изложен выше в гл. I.

Аналогично работам [5—7 ] было проведено исследование [11]. Полученные экспериментальные данные, а также обобщенное уравнение для вычисления х* хорошо согласуются с результатами работ [5—7]. Относительно температурного кризиса х* точка зрения авторов [11] сводится к двум предположениям: с ростом температуры либо меняется знак теплового эффекта реакции дегидратации H2NCOONH4, либо в жидкой фазе достаточно глу­боко протекает эндотермическая реакция диссоциации карбамата аммония.

При проектировании многих производств карбамида в свое время большую роль сыграла известная обобщенная номограмма Фрежака [12] зависимости х* — t — L— W. Эта номограмма была составлена полуэмпирически, на основе упрощенных пред­ставлений о термодинамике синтеза карбамида и небольшого объема экспериментальных данных. Опубликованная позднее номограмма [13], составленная по тому же принципу, отличается от первой лишь геометрической структурой. Сопоставление значе­ний х*, снятых с обеих номограмм, с надежными эксперименталь­ными данными [6, 7, 11 ] приводит к заключению [5], что указан­ные номограммы пригодны лишь для ориентировочной оценки величины х* и не могут быть использованы при проектировании современных крупных агрегатов синтеза карбамида. Последний вариант номограммы [14], — как установлено тщательным анали­зом []5] — в температурном интервале 190—210 °С, представляю­щем наибольший практический интерес, не обеспечивает удовлет­ворительной точности. Номограммой можно пользоваться лишь при температурах до 190 °С.

В ряде случаев, например, при изучении теплофизических, коррозионных и прочих свойств системы NH3—С02—CO(NH2)3— —Н20, при получении различных продуктов на основе карбамида, для вычисления х* нельзя воспользоваться уравнением (II.1). В соответствующих опытах на лабораторных установках в ста­тических условиях регламентированному изменению доступна ве­личина рсм, а не Р. Поэтому на основе экспериментальных данных, полученных при исследовании системы NHS—С02—CO(NH2)2—Н20 в статическом автоклаве, с использованием наиболее достоверных литературных сведений авторами [16 J составлено обобщенное уравнение зависимости х* — t — рсм — L — W:

Х* = 0,0413* — 14,07рсм— 11,2061 — 16.33Г - f 0,02372Lt — — 6,21Sp—J +44,48 In L - f 7,340LpCM -f - 30,60 (11.2)

В отличие от уравнения (II.1) здесь х* — степень превращения всего исходного количества С02 в карбамид, %.

Уравнение (II.2) составлено по данным 102 опытов, охваты­вающих следующие интервалы изменения переменных: t = 160 + 200 °С; рда = 0,Зч-1,0 г/см3; L = 2-5; IF = 0-1,5. При этом /> = 0,990; ах* = 1,6%.

Равновесное давление. Зависимость величины Р* от условий синтеза, как видно из табл. II.2, изучали многие авторы [171. Тем не менее, область параметров процесса L > 2 и W > 0, представляющая наибольший практический интерес, до недавнего времени оставалась неизученной.

Уравнения для вычисления Р*, предложенные в работе [18], применимы только при L = 2, IF = 0. Составленное позднее уравнение [19], которое используется в кинетических и техноло­гических расчетах [1 ], относится к W — 0 и получено по экспе­риментальным данным в сравнительно узких интервалах изме­нения t и рсм.

Выразить зависимость Р* — f (t, рсм, L, W) для широкого интервала параметров в виде одного обобщенного уравнения не представляется возможным: функция чувствительна к степени химического взаимодействия реагентов; частные зависимости Р* — L при неизменных t, рсм и W имеют экстремальный характер; в области параметров, представляющей практический интерес, может изменяться число компонентов системы и возможны пере­ходы системы из гетерогенного состояния (жидкость—газ) в гомо­генное (жидкость либо газ) [17, 20—23].

В работе [24] путем обработки результатов систематических измерений равновесного давления [20—22] приведены уравнения (II.3)—(II.5) для вычисления равновесных значений Р:

= — 31,945* — IО2-3965,1 Г1 +■ 0.05820*2 + 310, III +938,99L"1 — -25,87L2 - f 0,6719Г - 3017,6рсм -99,ОЗер-1 + 1998,7р2см + 6247,8 (II.3)

Pf~r = — 1,5810/ + l0-3-5,1730«f2 + 3,5030pCM + [,669L-

— 0.4565Г — 0,981651T2 + 120,98 (11.4) Pf~r = - 2,1796* + 10-3-7,078^ + 0,33275pCM - 32,3031 +

+ 4,8638І2 + 0,4148Г +225,98 (II.5)

Основные характеристики этих уравнений сведены в табл. II.3.

Кроме того, составлены уравнение (II.6)—(II.9) для вычисле­ния Lmm, Ргр, ргр, trys: Lmin — величина соотношения NH3 : С02, отвечающего [17, 20—22] минимуму на кривой Р* — L при задан­ных t, рсм, W\ Ргр, ргр, £гр — параметры системы [20—23] на границе перехода из двухфазной области (жидкость—газ) в одно­фазную (жидкость). Основные характеристики уравнений (II.6)— (II.9) помещены в табл. II.4.

Если заданное значение рсм > ргр, для вычисления Р* следует использовать уравнение (II.3), если же рсм < ргр, необходимо предварительно вычислить Lmin. При L > Lmln для расчета Р* служит уравнение (II.4), при L < Lmin — уравнение (II.5).

Уравнение (II.8) выполняет не только вспомогательную роль, но и совместно с уравнениями (II.7) и (11.9) представляет самостоятель­ный интерес, так как для многих технологических целей [20—23 ] необходимы сведения о параметрах рассматриваемой системы при изменении фазового состояния.

Плотность смеси в однофазной области (жидкость) рж можно вычислить по уравнению:

Рж= 10~3- 8,928/ —■ 10~5-2,912/2 + Ю~4-2,5/38Р-1- 10'* ■ 1.4661Р2 — — 0,25651 + 10~2-2,085L2 — 10"2-1,246Г + Ю'?-3,587ІГ2 + 0,9066 (11.10)

Основные характеристики уравнения (11.10) приведены в табл. II.4.

Объемные соотношения жидкой и газовой фаз. Для мно­гих технологических расчетов необходимо располагать сведениями о величине объемной доли жидкости ср* (в %) или газа в равновес­ной системе NH3—С02—CO(NH2)2—Н20. Зная величину <р*, можно вычислить плотность, сжимаемость, модуль упругости каждой из фаз и газожидкостной смеси в целом.

На основе выполненных систематических измерений величины ф* составлено [25] следующее обобщенное уравнение зависимости Ф* ~ t - Рсм - L - Г:

Ф* = — 0,0165* + 63,9рсм +11,14LpCM + 5,9р2„ — 0,3L + 0,6Г — 2,4 (11.11)

Уравнение (11.11) получено по данным 85 опытов в следующих областях параметров: t — 170—210 °С; рсм = 0,3—0,9 г/см3; L = == 2—6; W = 0—1. При этом гф = 0,992, 0ф = 2,59%.

Массовые соотношения жидкой и газовой фаз. Для вычисле­ния массовой доли жидкости в равновесной системе т]з* (в %) необходимо располагать сведениями о равновесных составах фаз.

Соответствующие экспериментальные данные (полученные, в основ­ном, при W — 0) в виде констант равновесия реакций представлены в [26]. По этим же данным было составлено [27] уравнение зависимости г|э* — t — рсм — L (при W = 0):

I|>* = — 0,50Н -f 0,408*рсм + 0,0372ifL - f 22,2рсм —

— 44,9р|м + I0.02L —3,18L2 + 0,193L3+ ИЗ,9 (11.12)

Для уравнения (И. 12) гф = 0,989; = 1,02%. Однако для большинства распространенных в промышленности технологических схем характерны значения W > 0. В связи с не­достаточным количеством сведений по составам фаз рассматривае­мой системы при W > 0 величину Я|) можно вычислить лишь приближенно. Предложены [27] следующие полуэмпирические методы.

При L = 2 величину г|% можно вычислить по уравнению

^ = 100_________ (ІОО-ФНІОО-ФГ) ,

Luu (! - J - 0,2308IF) (100 — ф) ( а>

Где гр — определяют по уравнению (11.12), а ф и ф^ — по уравне­нию (11.11).

При L ^ 3,5 рекомендовано уравнение:

Г)),!/ =100 — (100 — фіі/) —(11.14) Pw

Где pnh, — плотность чистого газообразного NH3, г/см3, при заданных значениях t и Pw; — плотность газожидкостной смеси, г/см3.

В случае 2 < L < 3,5 и t < 200 °С значения легко опре­делить графической интерполяцией расчетных данных, получен­ных при L — 2 и L 3,5.

Плотности сосуществующих фаз. При изучении состояния системы NH3—С02—CO(NH2)2—Н20 в случае проведения опытов в статических условиях величина рсм, г/см3, выбирается независи­мой переменной. При заданном (постоянном) объеме автоклава величина рсм целиком определяется количеством загруженных исходных реагентов; в то же время рсм является функцией t, Р, L, W, если последние выбрать в качестве независимых переменных.

Зная величину рсм, можно вычислить плотности сосуществую­щих жидкой (р;к) и газовой (рг) фаз, пользуясь соотношениями: •ф

Рж=~ Рсм (11.15)

100 —'Ф /ТТ 1СЧ

Используя полученные экспериментальные данные [19] по зависимости Р — t — рсм — L при W = 0, а также наиболее во надежные литературные данные, авторы [27] составили следую­щее уравнение:

Р*м= _ 10~3-9,550* + 10-5.1,8335*2 + 0,3110L — 10~2-3,4540L2—

— 10-4-6,3340LP+10-5-1,5918*Р— 1,3357Р~Ч - 1.3996 ' (II.17)

Уравнение (11.17) получено по данным 64 измерений в интерва­лах t = 150—220 °С; Р = 10—100 МПа, L = 2—6; при этом гр =

— 0,980, ор = 0,019 г/см3. Этим же уравнением пользуются и для ориентировочной оценки значений в двухфазной области (жидкость—газ). Отметим, что выше были приведены также урав­нения для вычисления ргр — на границе перехода из двухфазной области жидкость—газ в однофазную область — жидкость (II.8) и рж — в однофазной жидкостной области (11.10).

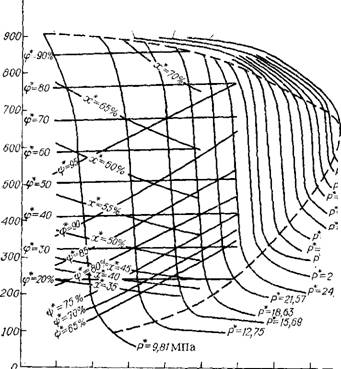
Диаграмма термодинамических свойств системы NH3—С02 —СО (NH2)3—Н20. В результате обработки экспери­ментальных данных с использованием приведенных выше уравне­ний авторы [28] построили диаграммы, наглядно отображающие функциональную связь и закономерности изменений х*, ер*, гр* в двухфазной области жидкость—газ, а также Р* при различных значениях t, рсм, L., W. Одна из диаграмм изображена на рис. II.2. Она относится к представляющим наибольший практический интерес значениям L и W. Семейство х* — кривых на диаграмме ограничено пределами изменения температуры t, для которых справедливо соответствующее расчетное уравнение. Поскольку функция х* — f (t) в интервале 190—210 °С проходит через максимум, в случае экстраполяции значения х* при t > 200 °С некоторая погрешность неизбежна. Прочие функции: ф* — t и if* — t, — по-видимому, можно экстраполировать в пределах 10—20°. Следует отметить, что все кривые на диаграммах в области значения рсм < 0,3 получены путем экстраполяции.

Пунктирная параболическая кривая делит диаграмму на три области: однофазная — газ (под нижней ветвью), однофазная — жидкость (над верхней ветвью), двухфазная — жидкость—газ (между ветвями).

Как видно из приведенной диаграммы, в двухфазной области даже вблизи границы с однофазной областью (газ) г|э* превышает 50% и достигает 95% задолго до границы с однофазной областью (жидкость). Из этого следует, что рассматриваемая функция мало­чувствительна к фазовому состоянию и не пригодна для аналити­ческого определения пограничных условий. Созданные диаграммы могут быть использованы в технологических расчетах, при изуче­нии теплофизических, коррозионных и прочих свойств системы NH3—С02—CO(NH2)2—Н20, а также при получении различных продуктов на основе карбамида.

Равновесные составы фаз в системе NH3—С02—СО (NH2)2—Н20. Подробно изложенные в работе [1 ] экспериментальные данные Болотова и ряда японских исследователей по равновесным соста­вам фаз в системе жидкость—газ NH3—С02—C0(NH2)2—Н20
сохраняют свое значение и в настоящее время. Новых сведений за последние годы появилось в литературе очень мало.

Авторы [29] измеряли парциальные давления компонентов системы при і — 20—80 °С, а также изучили зависимость степени гидролиза карбамата аммония от состава раствора и температуры в интервале 0—30 °С. Эти исследования имеют лишь теоретическое значение.

Авторы [4 ] определяли составы жидкой и газовой фаз, а также плотности и объемные соотношения жидкости и газа при t = = 150—200 °С; Р = 8—20 МПа, рсм = 0,53 г/см3, L = 2 и W < 0. В этой работе в газовой фазе равновесной системы, наряду с NH3, С02 и Н20, измеряли содержание CO(NH2)2. Например, при 170 °С, рсм = 0,53 г/см3, 1 = 2 и W = 0 массовое содержание CO(NHa)a в газе составило 1,6%.

Характеристики системы NH3—С02—CO(NH2)2—Н20 в иссле­дованиях [4] существенно отличались от параметров процесса 62
в узле синтеза промышленных агрегатов. Это несколько снижает практическую ценность рассматриваемой работы на современном этапе, хотя как было указано ранее, важное перспективное ее значение не вызывает сомнений.

Описание равновесия синтеза. Длительное время для практи­ческих целей пользовались термодинамической моделью системы NH3—С02—CO(NH2)2—Н20, предложенной Фрежаком [12]. Исходя из этой модели, авторы [10] с использованием эмпириче­ских уравнений [18] зависимости Р* — t — рсм составили для L = 2 и W = 0 уравнение зависимости х* — f (t, рсм). Последнее удовлетворительно описывало опытные данные только в сравни­тельно узких областях параметров. К настоящему времени на­коплен обширный экспериментальный материал, который не укладывается в рамки модели Фрежака и ее более поздних моди­фикаций [10, 13, 14].

Попытка составления математического описания равновесия реакций при синтезе карбамида была недавно предпринята в работе [23]. Предложенную авторами модель нельзя считать удачной, поскольку в качестве одного из основных ее элементов было использовано рассмотренное нами выше уравнение из работы [14] для определения х*. Наиболее обоснованное термодинамическое описание процесса синтеза предложили авторы [26]. Эта работа сохраняет свою актуальность до настоящего времени.

Для многих практических целей равновесные составы фаз в системе, образующейся при синтезе карбамида, можно вычис­лять, исходя из значений х*, а также приходящихся на жидкую фазу массовых долей (в % от общего количества в системе) NH3—Anhs. СОа в свободном и связанном виде—ХСо2 и Н20—^н2о - В расчете на 1 моль исходной С02 при равновесии справедливы уравнения:

Чн,= L~"NhM00 (II.18)

*со, = 0-««>,) 100 (ПЛ9>

W+ 0,0\х* (1~п' )— л - п н2о = — Л... „ „. * /■ ;—г^ 100 (п'2°)

Г + 0,01**(1-лШ2)

100 (11.21)

Пк

1 - "со,

Где п^н„, п'со2 и n'Hz0 — число молей компонентов газовой фазы; пк — число молей карбамида в жидкой фазе.

Авторы [30 ] с использованием полученных экспериментальным путем значений х*, а также литературных данных по равновесным

Составам сосуществующих фаз составили следующие Интерполя­ционные уравнения (при W = 0): ХШз = 10-2.8,509* — 0,3018*рсч + 10-4-5,506*2 + 129,2рси —

— 44,60рс2м + 0.8351L - 0.4742Z.2 + 10"-2• 4.207L3 + 35,32

Г = 0,976; о = 1,08% (П.22)

?.СОг = 80,26рсм — 36,92р2м— 0.4797*+ 10~3-6,I42*L + + Ю-8 -1,123*2 + 21.84L — 4.173L2 + 0.2442L3 + 69,91 (11.23)

Г = 0,985; 0=1,59%

Чо = -0,1517* - Ю-4-2,655*2 + 37,29Рсм - 45,95р2м + 5,810р|м -

— 4,006L + 0,1803*рсм+ 0,02287*1+ 105,134 (11.24) г = 0,991; о = 0,44%

Тепловой баланс процесса синтеза. Подробные тепловые рас­четы процесса синтеза, по результатам которых были построены диаграммы и составлены обобщенные уравнения, описаны в работе [30]. Из-за отсутствия в литературе термических характеристик плава синтеза карбамида и рециркулируемого раствора угле - аммонийных солей (РУАС) теплоемкости этих потоков вычисляли [30] по правилу аддитивности с использованием некоторых эмпи­рических закономерностей и уравнений квантовой теории тепло­емкости. Недавно теплоемкости упомянутых потоков были изме­рены [31 ] при 25 °С. Использование надежных значений теплоєм­костей позволит повысить точность тепловых расчетов процесса синтеза карбамида.