Равновесие газ—жидкость в частично открытой системе NH3—С02—Н20— CO(NH2)2 с заторможенными реакциями превращения карбамида
На практике система считается частично открытой, если число компонентов с постоянной массой в ней меньше числа фаз. Вариантность такой частично открытой системы совпадает с вариантностью закрытой системы [4]. Это дает основание описать равновесие частично открытой системы, не выходя за рамки классической термодинамики. Такая возможность заложена в методе Гиббса, в котором закрытая система' представлена совокупностью открытых систем. Пусть закрытая и открытая системы имеют одинаковый закрепленный объем Vа. При постоянной температуре для закрытой системы справедливо [51:
Будем считать, что закрытая система отделена непроницаемой перегородкой от некоей другой закрытой системы, способной изменять объем. Заменим непроницаемую перегородку на полупроницаемую, через которую может проникнуть только компонент /. По отношению друг к другу исходные закрытые системы превращаются в открытые, но вместе по-прежнему представляют закрытую систему. В результате перехода компонента изменяются Р, V, Ц/ по (1.43) в образованной закрытой системе, что распространяется и на составляющую ее открытую систему с объемом Vа. Заменяя полупроницаемую перегородку на непроницаемую, получаем закрытую систему с объемом У0, состояние которой отличается от первоначальной закрытой системы, что является единственно только результатом изменения ее массы при переходе компонента /.
Пусть в исходной системе содержалось молей компонентов и а'долей от этой суммы удалилось при перемещении компонентов /, k и т. д. (меняя перегородки, можно переводить поочередно все прочие компоненты). Если текущее число перевода всех компонентов равно s, в каждой вновь получаемой закрытой системе
S
Будет содержаться (1 — а') (1 — а")... = П (1 — аг) мо-
Г=1
Лей. Отсюда, полагая, что аг мало, находим число молей в результате перевода г компонентов и изменения состояния исходной системы s раз:
S а
InS"=in2"°+2,n _ in S п°+1d ln ~а)
Г=1 О
Т. Є.
(1.44)
8S
А2 = As In (Р/Р0)
|
1,00 |
|
0,2 -0,! " О \g(P/P°) |
|
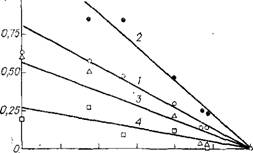
Рис. 1.9. Сравнение экспериментальных данных с графиком функции по уравнениям (1.46) и (1-47) прн Р=2-5МПа, Т= 373-433 K, X°jkl= = = 0,524, А'» а = 0,084, Х0ИгО = 0,257, X» = = 0,1361 |
|
VH36 , NH3 |
|
1 - а |
A* = X01.Aj + X0kAk + X0lAl
Последнее является степенью отгона суммы молей компонентов из открытой системы, которая описывает изменение ее состояния без нарушения требования термодинамики закрытых систем. Эта величина связана с ctjik>l компонентов следующим образом [19]:
Xi
|
Доли компонента до и после его выведения из системы. Далее предположим, что зависимость от V в окрестности V0 можно описать уравнением для идеальных систем. Пользуясь (1.43) и суммируя (интегрируя) потерю массы при переходе трех компонентов /, k, I, находим: ■ A/>Klln(P/P°) (1-46) (1.47) (1.48) |
Где ху, Xj — мольные
|
|
Где P° — давление в исходной закрытой системе; Р — в конечной закрытой системе при той же температуре; Ajik:l> Л2 — не зависящие от Р, Т, X°it k, і величины, отражающие способность компонентов покидать исходную закрытую систему.
|
(1.49) |
Уравнения (1.46—1.48) проверили по экспериментальным значениям a,, ki и а2 при Р = 2 — 5 МПа, Т = 373 — 433 К и X°jt k, и отвечающим составу «плава синтеза», зафиксированному в производстве [13, 19]. Величины Р° вычисляли из вспомогательного уравнения, предварительно полученного корреляцией экспериментальных значений Р° в форме уравнения (1.42), [3]. Опыт подтвердил справедливость уравнений (1.46, 1.47), причем соответствие среднеарифметической взвешенной величины Лопыт и Л2 по (1.48) выполняется с удовлетворительной точностью (рис. 1.9). Поскольку при одинаковых Т величина Р/Р0 <1, значения Ajtktl и Л2 отрицательны. Если Р/Р0—> 1, из (1.47), разлагая логарифм в ряд и ограничиваясь первым членом разложения, находим:
■ Ах(1—Р/Р«)
Такое уравнение было ранее найдено чисто эмпирическим путем [3]. Полученные уравнения служат для оценки предельных величин степеней отгона летучих компонентов из «плава синтеза» при заданных давлении и температуре «плава дистилляции» в непрерывном процессе.