Технологическое оборудование машиностроительных производств
Графическое изображение уравнений скорости резания и подачи
Производим и продаем электроприводы ЭТУ, ЭПУ для двигателей постоянного тока, тел./email +38 050 4571330 / rashid@msd.com.ua
Для кинематических расчетов коробок скоростей и подач в металлорежущих станках применяют два метода: аналитический и графоаналитический. Оба метода позволяют находить величины передаточных отношений. Однако, как правило, используют только графоаналитический метод. Достоинством его является то, что он позволяет быстро находить возможные варианты решения, что дает большую наглядность и облегчает сравнение вариантов. При графоаналитическом методе последовательно строят структурную сетку и график частоты вращения.
Структурная сетка дает ясное представление о структуре привода станка. По структурной сетке легко проследить связи между передаточными отношениями групповых передач (групповой передачей называют совокупность передач между двумя последовательными валами коробки скоростей или подач). Однако сетка не дает конкретных значений этих величин. Она наглядно характеризует ряд структур в общей форме. Структурная сетка содержит следующие данные о приводе: число групп передач, число передач в каждой группе, относительный порядок конструктивного расположения групп вдоль цепи передач, порядок кинематического включения групп, диапазон регулирования групповых передач, число частот вращения ведущего и ведомого валов групповой передачи.
График частоты вращения позволяет определить конкретные величины передаточных отношений всех передач привода и частоты вращения всех его валов. Его строят в соответствии с кинематической схемой привода. При разработке кинематической схемы коробки скоростей или подач с вращательным главным движением должны быть известны: число ступеней частоты вращения Zшпиндeля, знаменатель геометрического ряда ср, частоты вращения шпинделя от щ до пг и частота вращения электродвигателя пм.
Число ступеней частоты вращения шпинделя Zпри наладке последовательно включенными групповыми передачами (в многоваловых коробках) равно произведению числа передач в каждой группе, т. е. Z= PaPbPc...Pk. Например, для привода, показанного на рис. 7, Z= =РаРьРс= 3x2x2= 12.
При заданном или выбранном числе ступеней ряда частоты вращения шпинделя число групп передач в каждой группе и порядок расположения групп можно выбирать различными. Этот выбор в основном и определяет конструкцию коробки скоростей и подач.
Для наиболее часто применяемых значений могут быть использованы следующие конструктивные варианты: 22
Z= 4 = 2x2;
Z— 6 = 2x3;
Z= 8 = 2x2x2 = 4x2 = 2x4;
Z= 12 = 3x2x2 = 2x3x2 = 2x2x3 = 3x4 = 4x3;
Z= 16 = 2x2x2x2 = 4x2x2 = 2x4x2 = 2x2x4 = 4x4;
Z= 18 = 2x3x3 = 3x2x3 = 3x3x2;
Z= 24 = 2x3x2x2 = 2x2x3x2 = 2x2x2x3 = 2x3x4 = = 2x4x3 = 3x2x4 = 3x4x2 = 4x2x3 = 4x3x2.
В станках с изменением вращения шпинделя по геометрическому ряду передаточное отношение передач в группах образуют геометрический ряд со знаменателем срх, где х — целое число, которое называют характеристикой группы. Характеристика группы равна числу ступеней скорости, кинематически предшествующих данной группе. Общее уравнение наладки групповых передач имеет следующий вид: іх' h ' :/3.../р = 1 : <рх: ф2*:
Для последовательного получения всех частот вращения шпинделя сначала переключают передачи одной группы, затем другой и т. д. Если в коробке скоростей, показанной на рис. 7, использовать с этой целью, прежде всего, передачи группы (А), затем группы (С) и в последнюю очередь группы (В), то соответственно этому порядку переключения группа (А) будет основной, группа (С) — первой переборной, группа (В) — второй переборной.
Для основной группы передач характеристика AJ>= 1; для первой переборной Группы X] = Ри ДЛЯ второй переборной группы Х2 = РР2 и т. д., где Pi и Р2 — соответственно числа передач основной и первой переборной группы.
Для конструктивного варианта привода, показанного на рис. 7 и принятого порядка переключения скоростей, можно записать структурную формулу Z= 3(1) х 2(6) х 2(3). В формуле цифрами в скобках обозначены характеристики груп п. Основной и различными по номеру переборными группами может быть любая группа передач в приводе. Поэтому наряду с конструк-
Г_
|
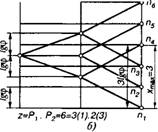
Р1=3; х0=1 Р^=2; х0=Р1=3 |
|
1 І |
|
Pz=3; *,=p,=2 p,=2;
Z=P1.P2=6=3(2).2(1) в) |
III
Тивными вариантами привода возможны также различные его кинематические варианты.
|
11 |
Во избежание чрезвычайно больших диаметров зубчатых колес в коробках скоростей, а также для нормальной их работы установлены следующие предельные передаточные отношения между валами при прямозубом зацеплении: 2 >/ > (1/4); отсюда наибольший диапазон регулирования групповой передачи будет (/тахЛтіп)пред = 2/1(1/4) = 8.
Отношение (/тахЛтіп)пред ИМЄЄТ Наибольшую ВЄЛИЧИНу ДЛЯ ПОСЛЄДНЄЙ переборной группы привода, следовательно, для коробок скоростей, где Хтах — наибольший показатель для последней переборной группы, Р— число передач в этой группе.
Для графического изображения частот вращения шпинделя станка обычно используют логарифмическую шкалу чисел. С этой целью геометрический ряд частот вращения п2 = Ліф; щ = пхц2 пА = а^ф3; nz = Ліф2 1 логарифмируют 1gn2 = lgfli + ^ф; 1gn3 = gnx + 2^ф; lg/24 = lg^ + +3^ф; ... ; lgnz = lgAij + (Z— 1)^. Откуда lg/i3 — 1gn2 = lg<p; lgn4 — 1gn3 = =21g<p; ...; lg^ = — 1 gnz-1 = І8Ф = const.
Таким образом, если откладывать на первой линии последовательные значения логарифмов частот вращения ль п2, л3,..., nz, то интервалы между ними будут постоянными и равными Igy.
Рассмотрим построение структурной сетки и графика частот вращения для коробки скоростей, кинематическая схема которой показана на рис. 8, а. Для принятого конструктивного варианта привода возможны два варианта структурной формулы: Z= 6 = 3(1)2(3) и Z= 6 = =3(2)2(1). В первом случае основой группы будет первая в конструктивном отношении группа передач, а первой переборной — вторая группа передач; для второго случая наоборот.
На рис. 8, б, в показаны структурные сетки приведенных структурных формул привода. Они построены следующим образом. На равном расстоянии друг от друга проводят вертикальные линии, число которых должно быть на единицу больше, чем число групповых передач. Также проводят ряд горизонтальных параллельных прямых с интервалом, равным логарифму ^ф (число горизонтальных прямых равно числу Z ступеней частоты вращения шпинделя). На середине первой слева вертикальной линии наносят точку О, из которой симметрично, в соответствии с числом передач в группах, по заданной структурной формуле проводят лучи, соединяющие точки на вертикальных линиях. Расстояние между соседними лучами должны быть равными где Xj — характеристика соответствующей группы.
Оптимальный вариант структурной сетки выбирают из следующих соображений. Выше отмечалось, что независимо от порядка переключений групповых передач диапазон регулирования последней переборной группы является наибольшим. Поэтому следует определить регулирования последовательных переборных групп для всех вариантов структурных сеток (при выбранном значении ф) и исключить из дальнейшего рассмотрения варианты, не удовлетворяющие условию
UUрел = Ф<П-|№И * 8-
Для варианта, показанного на рис. 8, б, Хтйх = 3, а для варианта, показанного на рис. 8, в, Хтах = 2. Вариант, приведенный на рис. 8, б подходит для всех значений ф, так как 2/2 — 1/3 = 8; вариант на рис.
|
3. Нормальные ряды чисел в станкостроении
|
|
4,25 |
42,5 |
||||||||
|
4,5 |
4,5 |
45 |
45 |
||||||
|
4,75 |
47,5 |
||||||||
|
5,0 |
5 |
5 |
50 |
50 |
50 |
||||
|
5,3 |
53 |
||||||||
|
5,6 |
5,6 |
5,6 |
5,6 |
56 |
56 |
||||
|
6,0 |
60 |
||||||||
|
6,3 |
6,3 |
6,3 |
6,3 |
63 |
63 |
63 |
|||
|
6,7 |
67 |
||||||||
|
7,1 |
7,1 |
71 |
71 |
||||||
|
7,5 |
75 |
||||||||
|
8,0 |
8 |
8 |
8 |
8 |
80 |
80 |
80 |
||
|
8,5 |
85 |
||||||||
|
9,0 |
9 |
90 |
90 |
||||||
|
9,5 |
95 |
|
425 |
|||||||||
|
45 |
56 |
450 475 500 530 560 600 |
450 500 560 |
500 |
500 |
560 |
|||
|
63 |
63 |
63 |
630 670 710 750 800 850 |
630 710 800 |
630 800 |
710 |
630 |
||
|
90 |
900 950 |
900 |
|||||||
|
1000 |
1000 |
1000 |
1000 |
1000 |
1000 |
8, в удовлетворяет всем значениям ф, за исключением ф = 1,8 и ф = 2, поскольку 1,78<3~1)2 > 8 и 2(3~1)2 > 8, на рис. 8, г, д показаны построенные для обоих вариантов структурных сеток графики частоты вращения при ф = 1,26, П = 160 мин"1, пъ = 500 мин"1 и пэъ = 1000 мин"1.
Графики частоты вращения строят в следующей последовательности: на равном расстоянии друг от друга проводят вертикальные линии, число которых равно числу валов коробки скоростей; на равном расстоянии друг от друга с интервалами ^ф (проводят горизонтальные линии, которым присваивают (снизу вверх) порядковые номера частот вращения, начиная с пх. Луч, проведенный между вертикальными линиями, обозначает передачу между двумя валами с передаточным отношением і = фш, где т — число интервалов lg<p, перекрытых лучом. При горизонтальном положении луча / = 1, при луче, направленном вверх, /> 1, а при направленном вниз /< 1.
Для данного примера (ф = 1,26) с учетом особенностей отдельных передач и значений предельных передаточных отношений /Мин. пред. = 1/4= = 1/ф6 и /мин. пред = 2/1 = ф3 строим для каждого варианта цепь передач для снижения частоты вращения от яэд до пх = 160 мин"1. Наиболее целесообразно при этом так разбить общее передаточное отношение цепи, чтобы сохранить более высокими частоты вращения промежуточных валов, в этом случае размеры коробки скоростей уменьшаются. Дальнейшее построение ведем, используя принятые варианты структурных сеток. Построенный график частоты вращения позволяет определить передаточные отношения всех передач коробки.
По найденным передаточным отношениям определяют числа зубьев зубчатых колес, следует иметь в виду, что в станкостроении межосевые расстояния, суммы чисел зубьев сопряженных колес, числа зубьев червячных колес и модули нормализованы. При постоянном расстоянии между осями ведущего и ведомого валов, при одинаковом модуле группы передач сумма чисел зубьев каждой пары зубчатых колес является постоянной величиной, т. е. IZ= Zx + Zq = Z3 + Z| = Zs + = ... = const.
Передаточное отношение пар зубчатых колес, находящихся в зацеплении, i = Zx/Za, h = Z3/Z4, /3 = %/Zb и т. д.; из уравнений Zx + Zf= = IZ и / = Zx/Z2 следует, что Z, = (1//, + 1)/IZ и Za = (1//2 + 1)/IZ. По этим формулам находят числа зубьев колес группы по заданной IZ. Передаточное отношение iu h и т. д. определяют по графику частоты вращения. По этим формулам находят числа зубьев колес группы по заданной IZ Передаточное отношение /ь /2 и т. д. определяют по графику частоты вращения.
Ряды частот вращения шпинделей, двойных ходов и ряды подач в станках. Для станков с вращательным главным движением окружная скорость резания зависит от числа оборотов шпинделя и диаметра обрабатываемой заготовки: К= ndn, где К— скорость резания в м/мин; 28 d — диаметр обрабатываемой заготовки в м; п — частота вращения заготовки в минуту.
При работе в различных условиях, особенно на специализированных и универсальных станках, возникает необходимость изменять скорость вращения шпинделя. Для получения оптимальных режимов обработки существует бесступенчатое регулирование числа оборотов. В первом случае в определенном интервале можно получить любое заданное значение. При ступенчатом регулировании частоту вращения шпинделя устанавливают в виде определенного ряда чисел оборотов. Механизмы, осуществляющие ступенчатое регулирование, проще по конструкции и надежны в эксплуатации, в следствие чего имеют наибольшее распространение.
Ряды чисел оборотов шпинделей чаще всего строят по закону геометрической прогрессии. Этот ряд удобен для осуществления экономических режимов резания. Достоинство его и в том, что он позволяет создавать сложные приводы из элементарных двухваловых механизмов, построенных тоже на основе геометрического ряда.
Допустим, что пи пъ — ряд чисел оборотов шпинделя. Если члены ряда расположить по возрастающей степени, то пх — /iiniu, a nz = =лтах; п и nz называют пределами регулирования: пх — нижним, nz — верхним, где z — число ступеней скорости вращения.
Если ф — знаменатель геометрической прогрессии ряда, то nz = =лг_іф = л1ф2~1. Решая это уравнение относительно ф, получим
|
|
Величина D = /wMim - Изменение
Скорости резания при переходе от одного числа оборотов шпинделя на другое — соединение по ряду при неизменном диаметре обработки называют перепадом скорости.
Его относительная величина для геометрического ряда (Vx — Vx+ х)/ /(К) = (пх — пк-1)/пх = (ф — 1)/ф = const. Значения применяемых в практике станкостроения знаменателей ряда и чисел оборотов шпинделей регламентированы. В основу нормализации положены, в частности, следующие принципы:
А) возможность получения рядов с различными знаменателями из основного ряда, имеющего наименьший знаменатель, путем отбрасывания отдельных членов ряда и сохранения основного ряда через 1,3, 5 и т. д.;
Б) десятичное повторение через «а» членов: пи п2, пъ, ..., 10пи 10л2, 10/ІЗ, ..., 100л,, 100/І2, 100/ІЗ... ДЛЯ ЭТОГО необходимо, чтобы /!* + ! = =ЛіФ°= 10/ij и ф = Ш.
Использование данного принципа позволяет иметь дело с меньшим количеством цифровых значений и строить таблицы чисел оборотов в пределах одного десятка;
В) удвоение через «Ь» членов: пи п2, ..., 2пи 2пъ 2я3, ..., 4пи 4пъ
4л3, ..., и т. д.; пь +1 = /*іФ*= 2пх и ф = .
Удвоение позволяет использовать в качестве привода двухскорост - ные двигатели переменного тока. Для того чтобы ряды одновременно соответствовали принципам бив, необходимо, чтобы: ср = ЛІТО = уі2 . Логарифмируя, получим lgcp= 1 /а • lglO = 1 /Ь • lg2 и, следовательно, b = 0,3 а. Для основного ряда принято значение фтш = 10* = 4Ш =
= ъ.
Нормальные ряды чисел в станкостроении приведены в табл. 3. Их значения принимают в качестве чисел оборотов шпинделей, подач, мощностей и т. д. Стандартные значения, полученные на основе указанных принципов, представлены в табл. 4.
|
4. Стандартные значения чисел
|