Техника наплавки алюминия бронзы на сталь

Методы определения сварочных напряжений и деформаций

Развитие техники, сопровождавшееся внедрение сварки в промышленность, обусловило необходимость изучения сварочных напряжений и деформаций.

Возникновение сварочных деформация и напряжений непрерывным нагревом свариваемого металла и его пластическим деформированием в процессе сварки, поэтому задача определения напряженно-деформированного

состояния сварных соединений является задачей термопластичности. Несмотря на то, что основное уравнение теории упругости для класса температурных задач были сформулированы более 100 лет назад Дюгамелем и Нейманом, а основные положения теории пластичности более 50 лет назад, решение задач определения сварочных напряжений и деформаций в общем виде связано с большими математическими трудностями. В первую очередь с выбором математической модели.

Процесс формирования сварочных деформаций и напряжений характеризуется рядом особенностей:

высокой концентрацией нагрева; . широким интервалом изменения температур;

изменением физико-химических свойств свариваемого металла; возникновением пластических деформаций.

Характер сварочных напряжений в значительной степени определяется геометрическими размерами свариваемой конструкции.

Отсюда следует, что построить математическую модель, которая в должной степени отражала бы перечисленные особенности сварочных напряжений и деформаций и в то же время позволяла бы довести решение задачи в общем случае до конкретного количественного результата возможно лишь с привлечением мощных вычислительных средств. Поэтому в ряде случаев бывает достаточно воспользоваться приближенными методами расчета, т. к. точные решения требуют больших затрат времени и средств для определения сварочных напряжений и деформаций используются расчетные схемы, в основе которых в той или иной степени находится ряд допущений.

В ряде приближенных методов расчетного определения сварочных напряжений и деформаций использовано допущение об одноосности сварочных напряжений. Во внимание принимают только напряжения ох> действующие в направлении, параллельном оси шва. Другие напряжения сгуи а2 считаются достаточно малыми.

Гипотеза плоских сечений предполагает отсутствие сдвига, т. е. yv=0.

При укладке шва сечения могут перемещаться, поворачиваться на некоторый угол, но не могут искривляться.

Гипотеза об одновременности укладки шва позволяет не рассматривать движение температурного поля вдоль оси Ох. Считается, что теплоту при сварке вводят сразу по всей длине шва, и в дальнейшем теплота распространяется только в направлении Оу, а если речь идет о круговом шве, то только в направлении оси г.

В некоторых случаях температурное поле вообще не рассматривается [69], а предполагается, что полоска металла, которая при сварке нагревалась до высоких температур, при остывании сокращается, встречая сопротивление усадки со стороны остального холодного металла. Принимают допущения о характере зависимости механических свойств металла от температуры. При расчётах используют схематизированные диаграммы зависимости предела текучести от температуры, а так же предположения о поведении металла как упругопластического тела. Нередко считают, что модуль упругости Е и коэффициент (X не зависят от температуры.

Для решения конкретных практических задач применяются следующие приближённые методы определения сварочных напряжений и деформаций: графоаналитические методы; методы, использующие аппарат теории упругости; методы, использующие аппарат теории пластичности.

К графоаналитическим относятся методы, разработанные Г. А. Николаевым, Н. О. Окербломом и К. М. Гатовским.

Наиболее ранними исследованиями сварочных напряжений и деформаций были работы Г. А.Николаева [91-94], в которых четко представлен механизм образования продольных деформаций и напряжений при наплавке валика на кромку полосы и при сварке пластин в стык. В данном методе приняты следующие допущения: имеются только одноосные продольные напряжения; поперечные сечения плоские; зависимость предела текучести от
температуры схематизирована; материал идеально упругопластический; модуль упругости Е и коэффициент а 'во всем диаппозоне температур приняты постоянными.

Решение задачи сводится к рассмотрению напряжений и деформаций только в двух сечениях пластины: в сечении, соответствующем наибольшей ширине изотермы 1150 °С при квазистационарном температурном поле, и в сечении после полного остывания пластины.

Собственные деформации (f^p+£ai) определяются как разность

наблюдаемых е„ и температурных ва деформаций:

В +£■ — в - в — в - сеАТ

упр пл н we н

В методе Н. О. Окерблома [95] приняты те же допущения, что и в методе Г. А. Николаева. Однако в отличие от последнего распределение упругих и пластических деформаций рассматривается не в двух, а во многих поперечных сечениях пластины на стадиях нагрева и охлаждения. В первом сечении начальные енач деформации равны нулю. Так как, считают, что до этого момента пластические деформации не происходили. Во всех последующих сечениях в качестве так называемой начальной деформации в уравнении (4.11.) в расчет вводят пластические деформации, которые имелись в предыдущем расчетном сечении. Тогда уравнение (4.1.) для сечения с номером п преобразуется к следующему виду:

(4.2.)

где Дг" - приращение пластических деформаций при переходе от сечения п-1 к п;

£яупр - упругие деформации в сечении п; в" - наблюдаемые деформации в сечении п; . в” - температурные деформации в сечении п; f"4 - пластические деформации в сечении п-1.

Существует разновидность данного метода, предназначенная для расчета деформаций напряжений в очень широких пластинах, для которых при

2В-юо можно принять єи=0. Если нужно определить только остаточные пластические деформации, то для пластин нет необходимости последовательно рассматривать п-ое количество сечений для определения временных деформаций. Достаточно определить упругие и пластические деформации для момента времени ДТ= ДТтах, когда пластические деформации максимальны, а затем решить задачу для полного остывания, используя пластические деформации при ДТ= ДТтах как начальные пластические.

При расчете напряжений и деформаций в случае быстродвижущихся источников теплоты используется гипотеза об одновременности укладки шва по всей длине.

Ширина зоны пластических деформаций 2ЬП вычисленная по методу

Н. О. Окерблома, получается больше, чем по методу Г. А.Николаева. Максимальные растягивающие остаточные напряжения в низкоуглеродистых сталях равны от в обоих методах.

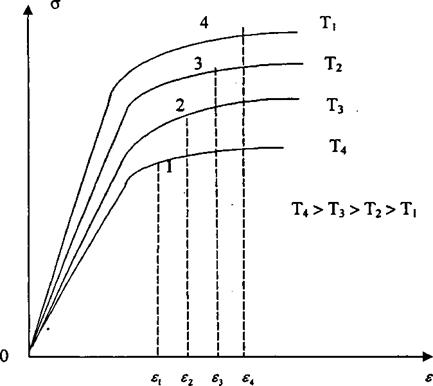
Метод К. М. Гатовского [96] отличается от предыдущего тем, что в нем вместо диаграммы идеально пластического тела используют диаграмму зависимости с упрочнением, полученные при разных температурах. Гипотезы об одноосности напряжений и плоских сечений сохраняются. Так же рассматривают ряд поперечных сечений на стадии нагрева и остывания пластины. Для определения упругих и пластических деформаций в каждом случае используют уравнение (4.2.) и метод последовательных приближений для отыскания правильного значения. Разделение собственных деформаций на упругие и пластические проводят с использованием действительных диаграмм и с учетом зависимости модуля упругости Е от температуры. Неопределенным в данном методе представляется определение напряжений на стадии высокотемпературной деформации. Предполагается, что возникает такое же упрочнение металла, как и упрочнение от деформаций при более низких температурах. При таком допущении металл должен последовательно проходить через состояние, характеризуемое точками 1-4 рис.4.6., хотя фактическое поведение металла будет иным. Оно может быть определено путем получения термодеформограммы.

т. е. фон, на котором происходят в области высоких температур значительно более сложные процессы деформаций, выходящие за пределы одноосной задачи. Эти методы не предназначены для определения поперечных деформаций.

Значительное место в исследовании сварочных напряжений и деформаций в тонкостенных оболочках принадлежит упругим решениям. Они являются первым приближением точного упругопластического решения.

В основе метода «упругих решений» лежат исследования академика А. А. Ильюшина. Упругое решение в деформациях и перемещениях нередко оказывается достаточным для определения перемещений при сварке.

Упругое решение, найденное для случая остывания неравномерно нагретого тела, когда начальное состояние тела перед остыванием можно рассматривать как не напряженное, дает качественную картину распределения остаточных напряжений, в некоторых случаях достаточную для правильных суждений о характере поля напряжений.

Упругие решения, конечно, не дают совершенно полного и правильного отображения картины распределения напряжений деформаций при сварке, если в действительности протекают пластические деформации. Степень неточности в каждом конкретном случае различна. Но она допустима для решения ряда практических задач [98].

Многие задачи определения напряженного состояния решаются с помощью методов, разработанных в теории упругости.

В работах К. П. Большакова выполнено приближенное упругое решение для подвижного температурного поля. Получение решения в общем, виде для перемещающегося температурного поля в процессе сварки весьма затруднительно в следствие сложных очертаний зон нагрева. Поэтому автором принято допущение, что форма изотерм температурного поля, возникающего при сварке тонкой пластины принимается в виде овала. Далее используется конформное отображение изотермы на внешнюю сторону окружности единичного радиуса. И, применяя математический аппарат плоской температурной задачи, определяются компоненты временных напряжений. Такой подход к решению зада^ с движущимся температурным полем обусловлен определенной схематизацией температурных процессов при сварке.

Одним из приближенных приемов описания остаточных напряжений в сварном соединении состоит в использовании аппарата теории упругости и привлечения экспериментальных данных, найденных для отдельных точек полученного соединения [99]. Применяя определенные аппроксимирующие зависимости, условия совместимости деформаций и дифференциальные уравнения равновесия, можно определить остаточные напряжения. Следует отметить, что точность вычисляемых, остаточных напряжений в первую очередь зависит от соответствия принятых в качестве функций распределения деформаций истинному характеру их распределения в рассматриваемом случае сварки.

К рассматриваемой группе относятся методы, предназначенные для решения неодномерных задач. Приближенными их называют. вследствие необходимости принятия допущений либо в отношении температурного поля, либо модели тела и многомерности поля напряжений. Точность получаемых результатов может быть различной, начина от сугубо качественных до количественных, которые можно использовать в нормативных расчётах.

Метод B. C. Игнатовной [100] предполагает мгновенную укладку шва по всей длине. Расчету остаточных напряжений и деформаций предшествует определение временных деформаций и напряжений на стадии нагрева. В качестве момента времени tp для их расчета принимается такой, когда наибольшая температура в какой-либо точке шва равна ТР. Температура ТР - это температура перехода из состояния, когда металл имел весьма низкий предел текучести и не способен сопротивляться пластической деформации, в состояние резкого возрастания предела текучести. Следовательно, температура ТР совпадает с температурой Тк рассматриваемой в предыдущем методе.

При распределении температур, соответствующем методу времени tp, методами теории упругости определяются временные условные напряжения.

По величине интенсивности вычисленных напряжений <yi определяется граница области развития пластических деформаций с учетом зависимости предела текучести металла от температуры. Вычисляются сами компоненты пластических деформаций на основе теории упругопластических деформаций. Поле, найденных пластических деформаций, в момент времени tp является полем начальных пластических деформаций, по которым затем для нормальной температуры тела определяются остаточные деформации и напряжения.

В основе метода Г. Б. Талыпова [101] лежит допущение, что «каждый металл резко теряет свою способность сопротивляться пластическим деформациям в определенном для. него достаточно узком интервале температур». Считается, что это происходит при определенной средней в этом интервале температуре Тк. Т. е. сг(=0, при температурах Т > Тк. Границы зоны, где металл нагрелся до Т = Тк, определяется по расчету температурного поля от движущегося источника теплоты при выбранном способе сварки.

Второе допущение заключается в том, что расчет проводится для стадии остывания, а процессы образования деформаций и напряжений на стадии нагрева не рассматривается. Процессы перераспределения теплоты и изменения температур в этот период не учитываются; считается, что области, в которых температура ниже Тк имеют все время начальную нормальную температуру Т0. И перед началом остывания свободны от каких-либо напряжений.

Таким образом, причиной образования остаточных напряжений и деформаций является температурное сокращение зоны, где температура выше Тк. Температурное сокращение этой зоны принимается равной а (Тк-Т0). Автором данного метода [101] предлагается так же другой подход, который состоит в следующем. Считается, что указанная зона приобрела начальные пластические деформации укорочения аг(Тк-Т0) в тех направлениях, где при нагреве было стеснено температурное расширение. Следовательно, по границам этой зоны и к остальным частям тела нужно приложить силы q противоположного знака, чтобы ликвидировать имеющиеся зазоры между

рассматриваемыми зонами. Образующиеся при этом деформации и напряжения считаются остаточными. '

Различие двух рассматриваемых подходов, по существу, заключается только в том, что в первом случае происходит равномерное сокращение металла зоны во всех направлениях, в то время как во втором случае сокращение может быть только в направлениях, по которым было стеснение при нагреве.

Для получения более точной сходимости экспериментальных и теоретически рассчитанных результатов, автор предлагает следующее: ввести упрочнение металла, а не принимать его идеальным упругопластическим; увеличить размеры рассматриваемой температурной зоны, где протекали пластические деформации, за пределы изотермы Т = Тк.

В работах В. А. Винокурова и Л. Г. Григорьянца [102, 103] разработан способ с использованием основных положений теорий упругости и пластичности, который определяет остаточные напряжения. с учетом подвижности источника тепла и зависимости свойств металла от температуры.

Исследованию кинетики сварочных напряжений и деформаций посвящены работы В. И. Махненко [77,79]. Автор сформулировал задачу кинетики сварных напряжений и деформаций при сварочном нагреве на основе теории неизотермического пластического течения. Для этого использовался метод последовательного выслеживания развития упругопластических деформаций на всем интервале нагрева - остывания конструкции. На каждом этапе решения находится с учетом истории нагружения методом «упругих решений», который позволяет свести нелинейную задачу к совокупности линейных. Однако сложность математического описания реальных процессов и необходимость большого количества экспериментальных данных затрудняет применение данного метода в инженерной практике.

На основании вышеизложенного, все существующие методы определения сварочных напряжений и деформаций используют различные гипотезы, упрощающие реальные процессы упругопластического

деформирования при сварке. В настоящее время не существует единой методики определения сварочных напряжений, а лишь имеются частные методики, предназначенные для решения определенного круга инженерных

задач.