ТЕПЛОПРОВОДНОСТЬ СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ
ВЫБОР ОПТИМАЛЬНОЙ МЕТОДИКИ ИСПЫТАНИИ
Выше уже отмечалось, что при определении коэффициентов теплопроводности при помощи приборов, основанных на использовании постоянного теплового режима (к их числу принадлежит и прибор ВТИ, примененный нами), зачастую имеют место методические погрешности, существенно искажающие результаты испытаний.
Во избежание этого нами были проведены специальные предварительные исследования, имеющие целью установить оптимальную методику испытании пи приборах рассматриваемого вида. Исследованпя были направлены в сторону разрешения важнейших в данном случае вопросов — ликвидации боковых тепло - потерь образцов, устранения влияния потери образцами влаги и ее перераспределения в процессе испытания, локализации воздействия контактных воздушных прослоек на границе между поверхностями образца и прибора. Проведение всех этих мероприятии и обеспечивает в основном надежность результатов испытаний. Помимо того, был также рассмотрен вопрос о температурном поле прибора и о наиболее вероятной степени точности испытаний
на приборе, (поскольку знание эгнх харакіеристніс необходимо при анализе и оценке результатов наших •жснерлмпптальпых данных в целом.
Выпор диаметра обрыщи. Выбирая диаметр образца, необходимо иметь 'В виду, что при меньшем иіамеїре легче ураипове - енть температуры при испытании; с другоіі стороны, больший диаметр парализует влияние возможной неравномерности строения материала образца. В принятом для проведення исследования приборе диаметр основного нагревателя равнялся 12 см однако известно, что не следует назначать диаметр образца точно по размерам основного нагревателя, так как образцы некоторых материалов в процессе испытания могут слегка обкрашиваться и по краям впоследствии образуются зазоры.
Для выбора оптимального диаметра образца были (проведены, специальные исследования с материалами различных объемных весов. Диаметр образцов сначала брали равным 15—16 см, а затем путем последовательных срезок доводили до величины 12 см, причем образец каждый раз заново испытывали. Высота образцов составляла около 3 см. Средняя температура испытаний равнялась 25°.
Помимо изменения диаметра образца варьировали также и диаметр холодильника прибора. Испытания были проведены с двумя различными холодильниками. Одни из холодильников имел диаметр, обычно применяемый їв приборах типа ВТИ, равный внешнему диаметру охранного кольца (рис. 1); другой холодильник был с уменьшенным диаметром, равным диаметру основного нагревателя прибора, т. е. 12 см. Результаты испытаний показали, что коэффициент теплопроводности повышается с увеличением диаметра образца; последнее несомненно связано с возрастающими при этом боковыми теплопотерями образца. Одновременно было установлено, что в случае использования прибора с большим холодильником величины I получаются более высокими, чем для образцов того же диаметра, испытанных на том же приборе, но с малым холодильником В связи с этим все дальнейшие испытания вели с холодильником малого размера, а диаметр образцов составлял 12,2—12,3 см.
Выбор высоты образца. Желательность увеличения высоты образца диктуется в первую очередь тем, что при этом возможно повысить точность результатов испытаний (поскольку рлзмор высоты входит в формулу для подсчета коэффициента тснлощю - водности—см. выше), а также в той или иной мере ослабить влияние возможной неравномерности структуры самого материала образца.
Однако, с другой стороны, необходимо иметь н виду, что с увеличением высоты образца затрудняется регулирование тем - пер а ті р и повышается длительность процесса испытания. Помимо того, существенное увеличение высоты образца неизбежно будет сопровождаться резким повышением теплопотерь с боковых сто - рои образца и процессе испытания, что, естественно, искали г ею релулыагы. . >іо обстоятельство и должно. по существу явиться решающим при выборе вьюны образца.
-Для выявления влияния высоты образца на величину коэф фнциеита теплопроводности были проделаны специальные исследования с материалами различного объемного веса. Испытыва - лись образцы диаметром 12,3 см и высотой от 6—10 до 1,7—3 см. Высоту образцов уменьшали путем их последовательной срез™ с обеих сторон по 'Мере производства испытаний. Средняя температура испытаний равнялась 2Г>°
Из результатов испытаний, приведенных в табл. 1, та первый взгляд нельзя сделать сколько-нибудь утешительных выводов, так как по этим данным получается, что с уменьшением высоты образца величина коэффициента теплопроводности непрерывно уменьшается и, стало быть, боковые теплопотери имеют место даже для образцов крайне 'незначительной высоты. Однако еще из опытов проф. О. Е. Власова [2] известно о наличии дополнительного термического сопротивления за счет воздушных зазоров, неизбежно имеющих - место между. поверхностями образца и прибора. Э [О так. называемое «переходное сопротивление» отражается. па экспериментально «слученной величине X, уменьшая последнюю, .причем уменьшение, естественно, имеет место тем в большей степени, чем меньше высота самого образца.
Таким образом, приведенные в табл. 1 данные о коэффициентах теплопроводности образцов разной высоты, на величину которых оказывает влияние, помимо возможных боковых тепло - потерь, также и переходное сопротивление, не могут непосредственно служить для выявления оптимальной высоты образца.
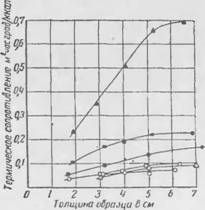
Более наглядная картина получается, если вычислить значения термических сопротивлений образцов и построить зависимость этих величин от высоты (рис. 2). Поскольку переходное сопротивление можно считать более или менее постоянным для образцов разной высоты (из одного и того же материала), то характер кривых на рис. 2 иллюстрирует уже непосредственное влияние боковых теплопотерь.
Как указывает проф. Д. Л. Тимрот [24], критерием, позволяющим судить об отсутствии боковых reiuoiiolvpi., является линейная зависимость термического сопротивления образца от его высоты. В случае же, когда боковые теплопотери начинают оказывать влияние, эта зависимость, естественно, приобретает криволинейный характер. Рассматривая рис 2 под этим vi.'imi зрения, обнаруживаем, чю при высотах образцов 1 Т> ( и и более в ряде случаев имеет место уже вполне наглядное огклоненне от линейной зависимости.
В внд этого при дальнейших испытаниях использовались только такие образцы, в которых высота равнялась 3 см с незначительными отклонениями в ту или другую сторону.
2-239
|
Таблица 1 Результаты испытаний образцов различной высоты
|
|
* Маловероятный результат; ■ расчет не принимается. |
Выбор перепади температур в приборе. В процессе испытания влага, сначала равномерно распределенная в образце, в силу общеизвестных положеніїІЇ должна ш той или пион степени переместиться от теплой поверхности образца к холодной. Поскольку в приборах, основанных на использовании постоянного теплового режима, процесс испытания довольно длителен, отмеченное выше явление при известных условиях может привести к тому, что у холодной поверхности образца скопится значительное количество влаги, переместившейся из той части образца, которая примыкает к нагревателю прибора. Естественно, что это явление может привести к получению искаженных результатов испытаний.
Очевидно, однако, что степень перераспределения влаги в образце должна находиться в непосредственной зависимости от величины температурного перепада в приборе. Для выяснения этого обстоятельства нами были проведены специальные исследования с материалами различных объемных весов и разной влажности. Максимальное влагосодержа - ние образцов составляло 21,5% (по оОьему) Образцы испытывали параллельно при различных перепадах температур — от 10 до 50° После испытания соответствующие образцы быстро распиливали пополам (по высоте) и затем определяли содержание влаги в каждой половине образца.
|
Условные обозначения: А - Пенобетон тенлиизоляциснпыО ■ - — «»— конструктивный • - Г ипсодар отливка Д ------- •> □ - Кирпич красный ° ■> — силикотньй |
|
Рис. 2. Термическое сопротивление образцов различной высоты |
Результаты испытаний приведены в табл. 2. Из этих данных видно, что в случае перепадов температуры, не превышающих 10 20°, влагосодержание в обеих половинах образца является практически одинаковым [2] и, следовательно, искажения результатов испытаний па теплопроводность при этом не может иметь места.
|
Ї- |
Здесь, впрочем, следует указать, что очень многие исследова
тели, пользовавшиеся приборами, основанными на принципе постоянного теплового режима, С ОТМСЧСМІНЬИМ ШІЛОІИІСМ совершенно не считались и вели испытании влажных образцов ври перепадах температур порядка 50—60° и выше; это, конечно, отразилось на достоверности полученных ими данных. Последнее обстоятельство обычно служит главной причиной нареканий в отношении результатов исследований, проведенных па приборах рассматриваемого вида [22].
В связи с изложенным для исследовании влажных материалов нами был принят в качестве постоянной величины температурный перепад в приборе, равный 15°. При этом перепаде, с незначительным отклонением в ту или другую сторону, велись все дальнейшие испытания. Последующая выборочная проверка подтвердила отсутствие сколько-нибудь значительной неравномерности распределения влаги в образцах после испытаний при указанном перепаде температур.
|
І а б л и ц а 2 Распределение влаги в образцах после испытания на теплопроводность
|
|
• В числителе дан процент влаги в верхней половине образца, в знаменателе-и нижней. |
Кривые распределения величии потери образцами влаги, построенные на основе результатов всех проведенных нами испытаний. Из этих данных явствует, что в наиболее часто повторяющихся случаях размер потери влаги был незначителен. Однако в отдельных случаях потеря достигал а 10— 15 % (и более) от общего содержания влаги в данном образце.
При испарении влаги затрачивается некоторое количество тепла, могущего повысить величину Q. вводимую п расчет при вычислении коэффициента теплопроводности по формуле (1), и, следовательно, исказить его значение. В связи с этим явилось необходимым выяснить характер протекания .процесса потери влаги. в образцах во время испытания.
Для этой ці'.'їн были проведены специальные исследования с различными материалами. Как уже отмечалось, установлению постоянного теплового режима. в образце предшествует некоторый период времени. Предстояло выяснить, когда, собственно говоря, происходит потеря влаги—в процессе ли установления постоянного режима или, наоборот, по его достижении.
Для выяснения этого обстоятельства образцы исиытывались двукратно. Один раз испытание производилось нормально, .і лругои раз — но сокращенному циклу, т. е. только до момента установления постоянного режима, после чего испытание сразу же прекращалось.
Таблица З
|
Потеря илаги образцами и процессе испытаний (при средней температуре 25 | 5 )
|
Результаты испытаний, приведенные в табл. 3, показывают, что в обоих случаях величина потери влаги примерно одинакова. Отсюда ясно, что потеря влаги в основном происходит в период, предшествующий установлению постоянного режима, и, следовательно, не отражается. на величине коэффициента теплопроводности.
Учет переходного сопротивления. Совершенно естественно, что, как бы тщательно не производилась отшлифовка поверхностей образца, добиться полного отсутствия воздушного зазора между .поверхностями образца и прибора ие представляется возможным.
С. И. Муромов [16] в своих исследованиях многослойной изоляции выяснил, что даже между двумя плотно прижатыми друг к другу шлифованными стеклами существует воздушный зазор с термическим сопротивлением, .равным г=0,0036 м2час град/ккал.
По данным проф. О. Е. Власова [2], величина термического сопротивления двух. воздушных зазоров между поверхностями образцов кирпича и медными плитками прибора. колеблется в пределах от R = 0,016 до R — 0,026 м2 час град/ккал.
Для выявления того, какая же величина термического сопро тивления воздушных зазоров между поверхностями образцов и прибора имела место в наших опытах, можно воспользоваться вышеприведенными результатами испытаний образцов различной высоты (табл. 1).
Если образцы имеют малую высоту, т. е. когда боковые потери тепла отсутствуют, то, пользуясь результатами определения коэффициентов теплопроводности двух образцов различной высоты
(Л| И hi), МОЖНО ВЫЧИСЛИТЬ ЦСЛІІЧШіу ПереХОЩЮГО іЧЧірої ІІІІЛеіІІІЧ,
«сходя из значений термических сопротивлений этих образцов (Я| и /v'v). Обозначим:
R— переходное сопріугніїїлеиие ні л обеих поиерхпос гях образца
|
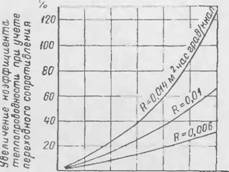
С,? о, ч 0,6 o, s /.о <,? Нсэффициент теплопроводности чналім час грав Рис. 4. Влияние переходного сопротивления на величину коэффициента теплопроводности при толщине образца 3 см |
(принимается одинаковым дли обоих образцов); X—действительный коэффициент теплопроводности материала образца (с учетом переходного сопротивления). Тогда
R* =
Решая эти уравнения совместно, находим R. Вычисленные таким путем значения переходных сопротивлений для разных материалов приведены в той же табл. 1. Как видно из этих данных, величина R колеблется в пределах 0,0062—0,014 м2час град/ккал, что, имея в виду опыты Муромова с шлифованными стеклами (по Муромову для двух зазоров R= 2 • 0,0036 = = 0,0072), во всяком случае свидетельствует о достаточно тщательной подготовке образцов в наших испытаниях.
Если учесть влияние переходного сопротивления при средней толщине образца 3 см, то, как видно нз рис. 4, значения коэффициентов теплопроводности, полученные непосредственно из экспериментов, в особенности для материалов с большими значениями /, подлежат весьма серьезной корректировке.
В связи с этим нами при последующей обработке экспериментальных данных все полученные и, опытов величины /. систематически пересчитывались с учетом постоянной величины переходного сопротивления, принятой равной (для обеих поверхностей образца) R = -- 0,01 лі-час град/ккал.
Поскольку фактические значения R для различных материалов неизбежно доллагм были отклоняться от вышеуказанной
средней 'величины (по краіміси мере в пределах, приведенных в табл. 1), то тем самым, естественно, были внесены известные неточное їй и окончательные значения ко (ффицш-н rem геилонр" водное ph. Однако из рис. 1 ницпо. что. иілчпіслию (тльніио ні точности имели бы мести, если бы влияние переходного сопротивления нами не учитывалось совершенно.
Температурное поле прибора. Для выявления действительного характера распределения температур по сечению образца в процессе испытания необходимо определить температурное поле при бора как для случая использования большого холодильника (обычного для приборов типа ВТИ), таи и для случая использования применявшегося нами малого холодильника (с диаметром, равным диаметру основного нагревателя. прибора).
Приняв высоту образца равной 3 см (в соответствии с высотой, принимавшейся нами при производстве всех испытаний), зададимся характерными точками поля, распределенными по прямоугольной сетке, при расстоянии между точками по горизонтали, равном 0,02 м, а по вертикали — 0,015 м. По сечению же образца сетку берем вдвое чаще (рис. 5).
Расчет пространственного температурного поля, обычно представляющий существенные трудности, в случае наличия оси симметрии, как показал К - Ф. Фокин [25], значительно упрощается. В данном случае осью симметрии является вертикальная ось прибора, а сам прибор и образец имеют цилиндрическую форму. Это дает возможность произвести определение температур в различных точках поля из условий теплового баланса, руководствуясь. законами прохождения потока тепла в теле цилиндрической формы. Так, например, для точки 18, находящейся внутри температурного поля, количество тепла, передаваемого к точке 15:
2лА30,015 Я і= (По •
In ■
То же, к точке 23:
_ 2^3 0,015
Ї2 — о~]2 V д8 23J»
Ln ~оДо~
То іже, к точке 17:
__ 7iA3 (0,112-0,092) Чъ ~ ~ Ш5 [3] ~~
То же, к точке 19:
____ ^3(0.11^-0,09?) ,у, v
Чі ~ ~ Щб ^ 18 ~
Из условия теплового баланса <7і + <7г + +'/4 =0, откуда находим выражение для tis.
Принимаем:
Коэффициент теплопроводности материала образца X -= 0,05 ккал/м час град коэффициент теплопроводности изоляционной засыпки ^-з = 0,05 . . . коэффициент теплопроводности стали (стенка кожуха прибора) Хс50,0 „ . коэффициент теплоперехода от поверхности кожу-
^,ха прибора (или засыпки) к воздуху а = 7,5 ккал! мг нас град
Температуру холодильника прибора 7"0 — 18е
Температуры нагревателя н охранного кольца прибора Т = Тк = 33'
Температуру воздуха в помещении лаборатории tB — 18*
Одновременно принимаем, что в средней части образца радиусом 0,02 м (ограниченной цилиндрической поверхностью, проходящей через точки а — б — в) имеет. место линейный ход температур. Принимаем также, что на холодной и горячей сторонах образца и примыкающей засыпки температура равна, соответственно, температуре холодильника и нагревателя прибора. Принимаем, наконец, что по линии точек г — д — е тепловой поток идет .нормально, независимо от влияниия соседних зон по вертикали. Таким образом, все граничные условия заданы.
Пользуясь описанным выше приемом, составляем выражения теплового баланса для всех точек температурного поля как в случае прибора с большим холодильником, так и с малым. Решая полученные системы уравнений, находим значения температур в различных точках поля для обоих случаев (рис. 5, а и 5,6).
Из приведенных данных видно, что, когда прибор имеет малый холодильник, то налицо приток тепла к боковой поверхности образца и, стало быть, через образец протекает дополнительное количество тепла, идущего от охранного кольца. Поскольку при подсчете а по формуле (1) учитывается только количество тепла Q, прошедшее через основной нагреватель, очевидно, что величина /., подсчитанная при этом значении Q, в действительности является несколько заниженной.
Наоборот, при пользовании прибором с большим холодильником имеет место утечка тепла через боковую поверхность образца за счет переохлаждения последней той частью холодиль - пика, которая расположена над охранным кольцом. J го оосгон - тслю'но приводит к завышению величины >, определенной на
Приборе С ҐІШІЬІІШ'М ХОЛОДИЛЬНИКОМ, ІІірОІїІШ /Ц ПСПІПІГЛІ. ПОП) ІІІЛ ЧЄІІ11Я "Kl »"■>! 1>|]>І 11 (1 KM ІТІІ "ГеПЛОПрОНОДШКЧ'Н.
Отсюда становится попятным, почему при пользовании прибором с малым холодильником экопериментальные значения получаются меньшими, чем определенные на приборе с большим холодильником (см. выше).
Найдем степень погрешности за счет неравномерности распределения температур по сечению образца, имеющую место при определении величины к & обоих этих случаях.
В случае прибора с малым холодильником средняя температура боковой поверхности образца:
F = 33 + (29,3 + 25.6 + 21,85) 2+ 18 = gg 5g0.
Приток тепла от боковой поверхности образца к цилиндрической поверхности радиусом 0,04 м, проходящей через точки 4-5—6 (со средней температурой 25,5°):
(25,56 — 25,5) 2 • 3.14 - 0,05 ■ 0.03 Q' ^ = 0,001395 к кал/час-,
Ln W"
Количество тепла, прошедшее через образец от основного нагревателя:
П 15.0-3,14-0.06»-0,05 п 000 Q = = 0,283 ккалчас.
Следовательно, погрешность
, 0,001395-100 , ,ч
Р = ------- jjggg----- = 0,49% (в сторону занижения к).
В случае прибора с большим холодильником средняя температура боковой поверхности образца
T" = 33+ (29,2+ 25,3+ 21.6) 2 + 18 = ^ 40.
Утечка тепла от цилиндрической поверхности радиусом 0,03 м, проходящей через точки /—2—3 (со средней температурой 25,5°) л боковой поверхности образца:
(25,5 — 25.4) 2-3,14-0.05.0.03
------ ,,„г---------------------- 0,00136 кка■ і час;
,п 1),0"Г
■погрешность:
= = 0>48„|(1 (I| fTO|)OIiy ;taulllIIKMimi I).
Таким образом, как при испытаниях с ЙЬМш'и. м холодплыш - ком, так и с малым холодильником погрешности, получающиеся за счет неравномерности распределения температур но сечению образца, крайне невелики, что является следствием. незначительной, по существу, степени этой неравномерности в обоих случаях. Отмеченное положение, как показали подсчеты, сохраняется и при использовании изоляционных засыпок с друїой теплозащитной способностью (например, при л3=-0,07—0,10 ккал/м час град), а также при иных значениях температур холодильника и нагревателя прибора (если, однако, сохранена неизменной принятая величина разности этих температур, т. е. Г— Т0= 15°).
Сказанное относится не только к результатам испытания образцов, обладающих малой теплопроводностью (X =0,05 ккал/м час град). Подсчеты показали, что при увеличении неравномерность распределения температур по сечению образца становится еще меньшей, а при больших значениях коэффициента теплопроводности образца Q - — 0,5—1,0 ккал/м час град) эта неравномерность вообще полностью исчезает, так как тепловой поток, идущий от нагревателя через образец, становится настолько мощным, что его не в состоянии отклонить никакие соседние влияния.
Очевидно поэтому, что с рассматриваемой точки зрения вопрос о. выборе типа холодильника, при принятых размерах прибора и толщине образца 3 см, вообще не играет особой роли. В наших испытаниях был использован малый холодильник, что дало определенные удобства при производстве испытаний и позволило избежать случайных погрешностей, могущих «меть место при недостаточно тщательной подбивке изоляционной засыпки в пространстве между свисающей частью большого холодильника и охранным кольцом (или при случайной осадке засыпки в этом пространстве в процессе испытания).
Точность испытаний на приборе. Ошибка, могущая произойти при определении коэффициентов теплопроводности на описанном приборе, представляет собой совокупность частных погрешностей, имеющих место при:
А) измерении высоты образца h;
Б) .нахождении количества тепла Q, проходящего через образец в процессе испытания;
В) определении. величины температурного перепада в образце (Т — Т0).
Подсчет отдельных составляющих "Каждой из этих частных погрешностей и их дальнейшее суммирование не представляют никакой сложности. Однако такой путь позволит установить лишь пределы, .в каких способно меняться макс и, м а л ь. н о - в о з - м о ж н о е значение величины общей ошибки, !в то время как нас
больше интересует наиболее вероятное значение этой величины. Дли последней цели произведем анализ ре «ульта тон всех лынолшчьпмч паїмп tu inaілмпіі
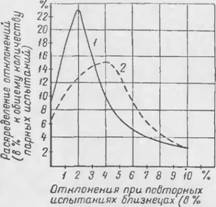
І І. і рис. <> изображены выровненные кривые распределения отклонении, имевших место при повторных йеныганняч-близне- цах. При этом приведены отдельные кривые для образцов, испытанных. в сухом и но влажном состоянии. При определении отклонений в результатах испытаний влажных образцов, в тех случаях, когда размер 'влажности в парных испытаниях 'недостаточно совпадал, отдельные результаты соответственно корректировались.
Из рис. 6 можно установить, что основная масса отклонений (70—80%) не превышает 4—5%. Среднее квадратичное отклонение по всем испытаниям сухих образцов равно 4,65%, а влажных образцов — 5,1 %.
Приведенные величины должны, по существу, достаточно близко охарактеризовать наиболее вероятные значения общей ошибки, если к ним присовокупить те погрешности, которые не могли войти в величину отклонений при повторных испытаниях-близнецах. Сюда относится погрешность, возникающая при измерении высоты образца (равная примерно 1 %), а также погрешность, имеющая место при определении значения Q, за счет неравномерности температур по сечению образца при малых значениях /-). Таким образом, следует полагать, что при определении коэффициентов теплопроводности на описанном приборе наиболее вероятная величина общей ошибки не превышает для основной массы испытаний ")-7%.
Этими данными нам и придется руководствоваться при последующем анализе результатов экспериментов, ибо совершенно очевидно, что с 'влиянием тех или иных подлежащих изучению факторов только тогда имеет смысл считаться, когда оно суще - твеино превышает точность испытаний на приборе.
|
К наименьшему результати по наждой ларе испытаний) Рис. 6. Кривые распределения отклонений при повторных испытаниях на теплопроводность I—сухие образцы: 2—влажные образцы |
|
(равная округленно 0,5%, да и то |
Полученные данные в целом позволили автору внести ряд юч. чечпй в методику определения /- на приборах, работающих г. п;>."., ui:iv постоянного теплового режима [10].