ТЕПЛОПРОВОДНОСТЬ СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ
ВЛАЖНЫЕ МАТЕРИАЛЫ
Вопросу о влиянии влажности уделял внимание целый ряд исследователей, поскольку наличие последней весьма существенно отражается на величине коэффициента теплопроводности. Однако,
58
Встречающиеся м литературе м іирііалі. і, .чарактеріАуіоіцнс влмн - ипе влажности на коэффициент теплопроводности, можно рассматривать лишь к качестве случайные и разрозненных данных, позволяющих судить о роли влажности вообще, по и большинстве случаев не дающих возможности уверенно использовать эти сведения в практических условиях. Немаловажная причина такого положения заключается в игнорировании многими из исследователей явлений перераспределения влаги в образцах, испытанных при больших температурных перепадах, о чем уже говорилось выше.
Установленные И. Каммерером общеизвестные зависимости, иллюстрирующие влияние влажности на коэффициент теплопроводности материалов неорганического происхождения, построены безотносительно от структурных различии, имеющих место среди материалов этой группы. Поскольку данные Каммерера широко популяризированы в литературе без надлежащей их критической оценки, на зтом вопросе стопі остановиться подробнее.
|
Кнал/м час град
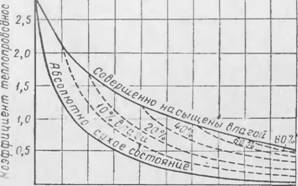
О w 20 30 W 50 60 70 80 90 100 % Пористость Рис. 23. Влияние влажности на теплопроводность неорганических материалов по Каммереру |
|
З Є |
|
Зависимость между влажностью и теплопроводностью для различной степени насыщения влагой и для материалов разной пористости (различных объемных весов). Хотя рассматриваемая диаграмма и обладает большой четкостью, нельзя не отнестись критически как к методике ее построения, так и к оценке послуживших для этого данных. |
Каммерер в своей посвященной рассматриваемому вопросу работе [35 -1] приводит анаграмму (рис. 23), иллюстрирующую
Как признает сам Каммерер, диаграмма эта не носит вполне точного характера. Нижняя кривая (для абсолютно сухпч материалов) построена по частичным опытным данным[4]. Чго же касается верхней кривой для материалов, полностью насыщенных влагой, то она построена только по концевым точкам—X = = 2,8 — для совершенно плотного тела и 0,50 ккал/м час град (вода). Общее же направление верхней кривой взято произвольно.
Данные, послужившие Каммерсру для построения промежуточных кривых, (Приведены в табл. 9. В той же таблице показаны, и величины коэффициентов теплопроводности, непосредственно снятые с рассматриваемой диаграммы. Естественно было бы предположить, что эти величины с достаточной степенью точности совпадают с результатами испытаний, послуживших для построения диаграммы. Однако мы видим, что для большинства точек расхождения достигают значительных размеров и по существу лишь всего 3—4 точки могут быть занесены в актив автора диаграммы.
|
Таблица 9 Теплопроводность неорганических строительных материалов По Каммереру
|
В другой своей работе Каммерер [35—3] опубликовал еще одну аналогичного рода зависимость, выведенную им из опытов с кирпичом, причем последнее обстоятельство не препятствует Каммереру рекомендовать эти данные для учета влияния влажности в любых неорганических строительных материалах, безотносительно от их структуры и объемного веса.
ЛвГОроМ ОЫ.'Ш НрОВеДОНЫ ОПЫТЫ! ПО В1.ШНЛЄІІІПО b. lIDIllUH ИЛ. ЇЖ
IKK 111 ll.'l КО >фф||ЦПЄІ1Т теплопроводности многочисленных мяте риалов ячеіісіого строения — различных по структуре и оОьем ному несу видов пепопето на и пористого кирпича, а также разнообразных мелкопористых материалов (табл. 4, 5 и 8).
Рис. 21 и 25, на которых показаны результаты испытаний части из этих материалов, достаточно наглядно иллюстрируют общий характер полученных зависимостей. Из этих данных можно установить, что зависимость между влажностью и коэффициентом теплопроводности характеризуется прямой линией, т. е., другими словами, прирост коэффициента теплопроводности на 1 % объемной влажности является постоянной величиной, не связанной с количеством влаги, содержащейся в материале. При этом, однако, нетрудно заметить, что линия характеризующая зависимость между влажностью и коэффициентом теплопроводности, часто является прямой только до некоторого критического значения влажности, а за тем приобретает кривизну, направленную выпуклостью вверх. Последнее свидетельствует уже о снижении интенсивности прироста X с дальнейшим увеличением содержания
Влаги. Совершенно такая же закономерность для различных видов кирпича наблюдается и в опытах Н. Г. Резцова [20], производившего эксперименты на приборе проф. Г. М. Кондратьева, повиди - мочу, j условиях незначительного перепада температур.
Обратимся к попытке объяснить это явление теоретическим путем. Для этого надо вычислит!, теоретические коэффициенты теплопроводности материалов ячеистого строения разной степени
Нлажпости и выяснить, какие закономерности при этом будут иметь место.
Вопросами теоретического определения величиньїі проводимости сложных тел того или иного строения занимался ряд исследователей. Однако ни одна из попыток разрешения этой задачи не увенчалась успехом. Если сравнить теоретические величины коэффициентов теплопроводности, вычисленные по формулам различных авторов, с надежными экспериментальными данными, то, как правило, получаются достаточно серьезные расхождения. Последнее имеет место даже для материалов с таким, относительно, правильным и равномерным строением, как пенобетон.
Объясняется это огромными математическими трудностями, возникающими при попытке
Непреодолимы. Эти обстоягельетва вмсеїе с иепзОежіюи ногич ностыо в назначении некоторых основных констант не нозво ля К) г <п.|Ги и вполне правильное п достоверное значение абсолют пых величин коэф(|)пцпепгов теплопроводности на основе каких-либо теоретических формул. В еіце большей степени это относится к влажным материалам. Однако, если ориентироваться не на абсолютные, а на относительные значения искомых закономерностей, то попытка вычисления величины X теоретическим путем может иметь определенный смысл.
В самом деле, если интересоваться отношением коэффициента теплопроводности материала во влажном состоянии, к таковому в сухом (например, определять, каким закономерностям подчиняется прирост коэффициента теплопроводности на 1% влажности), то значительная часть условностей, принимаемых в таком теоретическом расчете, сможет погаситься, н вероятно уластся получить более или менее правильную, если и не с количественной, то хотя бы с качественной стороны, зависимость.
Прежде чем переходить к такому расчету, необходимо рассмотреть возможные расчетные структуры, которые наиболее близко отвечали бы структуре рассматриваемого материала. В качестве последнего примем пенобетон, для которого нами произведено значительное количество экспериментов п который обладает относительно достаточно правильной и равномерной структурой.
Переходя к выбору последней, необходимо указать, что вся основная масса исследователей, пытавшихся вывести формулы для теоретического определения коэффициента теплопроводности, в качестве > ісментариой ячейки принимали куб с вписанной в него фигурой гой или иной формы (шар, тетраэдр, октаэдр и т. д.). При этом в зависимости от того, рассматривались ли зернистые или ячеистые материалы, излишек меж ту объемом куба и обы мом винсапной фигуры (теїа) рассматривался либо как во «туш - чая. либо как твердая фаза.
Ячейки пенобетона но форме вполне отвечают шару, и слело вательно, в качестве основной вписанной фигуры можно принять последний, полагая, что основная воздушная фаза имеет шаровидную форму. Если бы мы этим ограничились, т. е. приняли, что на каждый элементарный куб приходится только одна шаровидная ячейка, то это означало бы, что мы ориентируемся на кубическую укладку шаров. Однако такая укладка, как известно, является наименее плотной, и пористость материала с кубически уложенными шаровидными ячейками составляет всего приблизительно 52,4%.
Отсюда, зная, что объемный вес цементного камня, из которого состоят стенки ячеек пенобетона, равен в среднем 1,51 t/mz, получаем наименьший возможный объемный вес пенобетона равным
(I —0,524; 1,51 =0,63 т м*.
Такое положение совершенно противоречит дейсгинтемыюсгн, поскольку известно, что па практике іпіолпс возможно получить пенобетон объемным несом (),:ш О. ІІГ) г/мл
Наиболее плотная укладка іна|)он одинакового днамеїра, как известно, тетраэдрическая. В этом случае норпстость материала со сферическими ячейками составляет приблизительно 74,2%. При этом минимальный объемный вес пенобетона будет равен
(1 —0,742) 1,51 =0,39 т'м3,
Что значительно ближе соответствует действительности. На практике минимальный объемный вес может быть меньше этой величины, так как в действительности ячейки пенобетона неодинакового размера (хотя степень неравномерности их в большинстве случаев относительно невелика) и, стало быть, укладка шаров может быть еще более плотной.
Ограничимся, однако, рассмотрением структуры с шарами одинакового размера, расположенными в тетраэдрическом порядке, т. е. в таком порядке, при котором шары верхнего ряда укладываются в углубления, образованные каждыми четырьмя шарами нижнего ряда. Этому, кстати, довольно близко соответствует и действительная структура пенобетона.
Такому положению отвечают и условия структурообразования пенобетона, вытекающие из технологии его изготовления. Как известно, пенобетон получают, смешивая вяжущее тесто (или тесто из смеси вяжущего с заполнителем) с особой стойкой пеной, выдерживающей давление вяжущего, вплоть до его отвердевания и не разрушающейся в процессе смешения. Таким образом, пена является первичным формообразующим элементом при изготовлении пенобетона, причем промежутки между оболочками пены заполняются вяжущим тестом и в дальнейшем служат стенками ячеек, а сами ячейки сохраняют форму и расположение оболочек пены. Но, как известно, каждая из оболочек пены стремится к увеличению в объеме, и при этом, помимо общего роста всего объема пены, естественно, происходит наиболее тесное уплотнение взаимного расположения оболочек.
Таким образом, тетраэдрическое расположение ячеек пенобетона является структурой, достаточно оправданной, и может быть положено в основу теоретического расчета. При этой структуре каждую элементарную ячейку материала можно себе представить в виде куба, в центр которого вписана сферическая пора, а во всех восьми углах куба размещены дополнительные поры, по форме представляющие собой неполные четверти центральной сферической поры.
Величине 74,2%, то внутренний днамегр центральной поры (взле - мепг. ірпоіі нчеііке-кубе) ранен сто|)оііе куба Іхлп же пористе н> маіерналл метине, m цп. імеїр цгиіра.'іі. пічі поры мгпі. ш.іеігн п. стало быть, мерилом условной порппосгп материала может слу жнгь разность между величино* стороны куба и диаметром центральной поры.
Обозначим сторону куба через 2R, тогда величина условной пористости характеризуется значением aR.
Полагая ьлагу расположенной равномерно по стенке поры, толщину пленки влаги можем обозначить через bR. Эта величина будет характеризовать и степень условной влажности материала, пенимая под этой величиной только ту влагу, которая располагается в основных ячейках пенобетона (без учета влаги, могущей заполнить поры в стенках ячеек, к каковому обстоятельству мы еще вернемся).
Для теоретического определения коэффициентов теплопроводности материалов ячеистого строения воспользуемся приемом, разработанным проф. О. Е. Власовым [3,26].
Рассмотрим установившийся температурный режим в условиях плоскопараллельного теплового потока. Полагая, что температурное поле ограничено с боков плоскостями, абсолютно непроницаемыми для теплового потока, а с двух других сторон — изотермическими плоскостями, на которых поддерживаются постоянные температуры, причем тепловой поток направлен по оси х нормально к изотермическим плоскостям, приходим по Власову к значению величины теплопотери через рассматриваемый слой по уравнению
А(
Сіх
Flh
Где bt — температурный. перепад в слое;
—коэффициент теплопроводности на участке сечения с площадью Fr
Если разрезать нашу элементарную ячейку-куб по диагонали, то мы получим схематическое изображение, приведенное на рис 26.
Обозначим коэффициенты теплопроводности вещества стенок ячеек, воды и воздуха через >>т, Х„ и >.вз, а соответствующие им площади участков сечений через FT, F„ и Fn3. Для расчета нашу ячейку необходимо разбить на 5 слоев, в каждом из которых значения площадей, приходящихся на долю вещества стенок _-ек. воды и воздуха, подчиняются определенным закономер - н остям
(о
С другой стороны, согласно общеизвестным положениям, если обозначить средний коэффициент теплопроводности материала через имеем потерю тепла через половину элементарной ячейки
В том случае, когда fi2 > АС, имеем
/ I / , Л /і I Л" — /і (1
Где А, - /С.
Для решения задачи нам остается еще найти выражения для пористости и влажности материала. Эти величины, как уже указывалось выше, определяются значениями а и b (рис 26). Исходя из обычных 'геометрических положений, находим (при R — 1). пористость
Р _ '/з* [2 (1 — а) + (2 -- VT-а)" О + 2а } влажность
_ р 2/з" [2(1 - G - &)3 + (2 - /2- а - Ь)Ц +VT - 2A-2Ft)| (9)
Отсюда, зная в каждом отдельном случае значения пористости и влажности материала, можем определить при помощи формул (8) и (9) величины a, b и далее по формулам (7), (6), (5) и данным табл. 10 и Ц вычислить
Прежде чем переходить к вычислению коэффициентов теплопроводности пенобетона теоретическим путем, необходимо задаться предпосылкой в отношении распределения влаги в пенобетоне.
Стенки ячеек пенобетона состоят из цементного камня, пористость которого (при удельном весе пенобетона, равном в среднем 2,54, и объемном весе камня 1,51 т/м3) составляет
2,542~'-51 -100 = 40,6° ,..
Естественно принять, что эти поры в цементном K. IMHO, как наиболее мелкие, заполняются водой в первую очередь, причем пока они полностью не заполнены влагой, последняя в самих ячейках пенобетона еще отсутствует. Лишь после полного влагонасы - щения пор в цементном камне, т. е. в стенках ячеек, из ->ти пор начинает поступать влага в ячейки, распределяясь равномерным слоем по контуру поверхности ячеек.
Таким образом, в первый период увлажнения пенобетона, когда влага еще не проникла в ячейки и заполняет лишь (частично пли полностью) поры в цементном камне, при теоретическом определении величины среднего коэффициента теплопроводности лм можем принять, что материал сухой [Ь = 0), влияние же увлажнения отразится лишь на изменении вводимого в расчет коэффициента теплопроводности материала стенок ячеек--/,.
Когда же материал сгенок ячеек полностью увлажнится, т. е когда влажность стенок будет равняться 40,6% по объему, то. принимая соответствующую полному увлажнению цементного
камня величину коэффициента теплопроводности стенок ячеек лт> дальше уже в нашем теоретическом расчете будем определял. Хм, исходя из схемы влажного материала, причем величину Ь будем находить не по полному содержанию влаги в материале, а по разности между этой последней величиной и тем количеством влаги, которое находится в порах цементного камня и '.полностью их заполнило.
Поскольку мы опытным путем выявили влияние влажности на коэффициент теплопроводности цементной отливки (рис. 24), то для определения значення при разной степени увлажнения цементного камня, из которого состоят стенки ячеек, воспользуемся непосредственно этими экспериментальными данными.
Произведем определение теоретическим путем коэффициентов теплопроводности пенобетона разных объемных весов при различной степени влажности. В табл. 12 приведены значения влажности и величины принятые нами в качестве исходных данных при
|
Л |
Этих расчетах. Одно-
Временно принимаем '-„ =0,50 и = = 0,025 ккал/м час град.
Вычислив сначала коэффициенты теплопроводности пенобетона в сухом состоянии (при X, = 0,40 ккал/м час град), а затем во влажном состоянии >.т —см. табл. 12) определяем, исходя из этих данных, величины прироста коэффициента теплопроводности сухого материала на каждый процент объемной влажности.
Результаты подсчетов иллюстрируются рис. 27. Из этого графика мы видим, во-первых, что значения прироста коэффициента теплопроводности уменьшаются с увеличением объемного веса материала (к этому вопросу мы еще вернемся в дальнейшем). Во-вторых, здесь обнаруживается то же явление, которое уже отмечалось выше, а именно, что в первый период увлажнения величина прироста л не меняется, остается постоянной, а затем, начиная с некоторого момента, интенсивность прироста уменьшается.
Из рис. 27 видно, что этому моменту снижения интенсивности прироста как раз соответствует момент превышения общего содержания влаги в пенобетоне над степенью полного насыщения
|
•л Го |
1 |
1 1 |
1 |
С1 «О Г |
2,75 |
Ю Г |
||||
|
1р Со |
1 |
1 |
'С, п 1 п |
|||||||
|
Оо «5 СЧ |
1 |
1 |
1 |
О о |
1,85 |
1 |
||||
|
»о СЧ |
I 14,25 |
In Со |
СП JO |
•л / |
•о Га |
Ю |
1 |
31,5 |
Го |
|
|
1 21,5 |
1 |
40,6 |
1,85 |
1 |
||||||
|
Сэ сч |
•X - 'О СЧ СП |
,о ЭО |
СП га |
1 1.85 |
I |
30,2 |
1,49 |
25,2 |
1,32 |
|
|
16.! |
1 |
40,6 |
Ю Се |
1 |
1 |
1 |
||||
|
10,75 |
40,6 |
1,85 |
1 |
1 |
1 |
1 |
||||
|
О |
1 |
25,2 |
Сч со |
18,9 1,08 |
■о |
0,94 |
Со сч |
0,85 |
||
|
Иэ |
18,9 |
1,08 |
І Со ю (N — О 1 |
9,43 0,73 |
Ю 'со ю со t-*|o |
1 00 (М сч о СО о |
||||
|
- |
Г- СО |
0,53 |
І О Сч |
Оо -г О |
1,89 |
■^г |
Iq |
Ю О |
Со сч_ |
Га о" |
|
В том числе | на долю самих ячеек |
73,5 |
60,3 |
47,0 |
33,8 |
20.5 |
|||||
|
В том числе На долю пор в стенках ячеек |
Ю о |
Со |
21,5 |
26,8 |
32,25 |
|||||
|
Общая в пенобетоне |
1 а См —г ЭЭ |
-г 'О |
68,5 |
О О ^ |
52,75 |
|||||
|
Тона в су - хоч состоянии В ОТ/Л3 |
Т О |
CD О" |
Со о |
С> |
CN |
Влагой цементного к^мня, т. е. момент, когда излишек влаги начинает уже поступать в самые ячейки. Естественно, что чем материал более тяжелый, т. е. чем большая член, и общей пористости материала приходите» на долю пор и цементном камне стенок ячеек, тем этот момент отдаляется.
Таким образом, получается, что для материалов большого объемного веса (выше 0,8—1,0 т/м3) этот момент снижения интенсивности прироста коэффициента теплопроводности под влиянием влажности остается вообще почти не обнаруженным (в пределах исследованных размеров увлажнения материала).
Из рассмотрения рис. 24—25 видно, что даже для материалов с минимальным объемным весом момент перехода в кривизну линии, характеризующей влияние влажности, имеет место при величине последней не ниже 15% по объему. Но известно, что фактическое влагосодержание материалов, находящихся в обычных ограждающих конструкциях, даже в наиболее суровых условиях эксплуатации никогда не превышает указанной величины. Таким образом, с отмеченным выше явлением вообще можно не считаться и принять за основу при последующей обработке результатов экспериментов те значения величин прироста коэффициента теплопроводности, которые соответствуют первому периоду увлажнения материала. Эти величины и приведены в табл. 4, 5 и 8
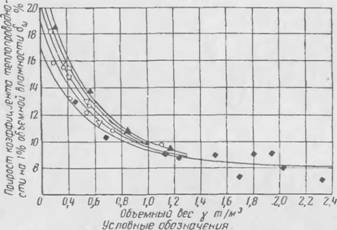
Если нанести значения добавок на влажность?>w (под этой величиной условимся понимать прирост коэффициента теплопроводности I на 1 % объемной влажности материала тз процентах) для исследованных материалов мелкопористого строения (табл.8) на график, в зависимости от объемного веса, то мы получим картину изменения рассматриваемой величины в весьма широком диапазоне плотности — от 0,4 до 2,3 т/м3 (рис. 28).
Как видим из этого графика, с увеличением объемного веса величина добавки на влажность падает. Это явление, отмеченное и в результате теоретических подсчетов (см. выше), является вполне закономерным, поскольку повышенному объемному весу соответствует возрастающее содержание плотного вещества, а отсюда растет и удельное значение последнего среди элементов, слагающих величину коэффициента теплопроводности материала.
Примем, после ряда предварительных прикидок, что кривая, характеризующая зависимость между величиной добавки на влажность t>w и объемным весом мелкопорнстых материалов, подчиняется закону
Тогда, экстраполируя нашу кривую до величины ■( = = 2,5 т/м3 — предельного объемного веса, практически возможного для материалов данной группы, находим с = 8,0. Далее, оперируя обычным способом наименьших квадратов, получаем
П — 8,0; її 0,3; b Г),7. Отсюда дли искомом зависимое:і мелкоиорпетык мап'|)іілл. і прнхо т. пм к с. вщuuih-mv выражению
Если нанести величины для исследованных материалов ячеистого строения (табл. 4 и 5) на тот же график (рис. 28), то оказывается, что точки, соответствующие группам материалов с определенными размерами ячеек, располагаются в общем достаточно закономерно.
|
♦ мептпарисгпыр материалы о - Материалы d= 0,45-0,71 мм V - — d= 0,81 - 1,Оп мм П •• el 1,2,4 1.38 мм Ж U 1,71 1,87 мм |
Рис. 28. Влияние влажности на теплопроводность неорганических материалов ячеистого строения
Очевидно, что характер взаимосвязи между величиной то бавкн на влажность н объемным весом в материалах с отпоен гельпо крупными ячейками в общем такой же, как и в мелкоио ристых материалах. Таким образом, в приведенную выше формулу для мелкопористых материалов может быть введен дополнительный член, характеризующий расположение кривых при материалах с различными размерами пор.
Для того чтобы формула имела при этом фншчсский смысл, лог дополнительный член должен обращаться в нуль при размерах ячеек, имеющих место в мелкопорнстых материалах, т. е. при среднем диаметре ячеек, равном 0,14 мм.
С другой стороны, нз характера распределения точек на рнс. 28 видно, что величина йи. р возрастает пропорционально увеличению диаметра ячеек. Прн этом по мере увеличения объемного веса влияние размера ячеек па величину заметно снижается, что вполне понятно, если учесть, что с повышением объемного веса уменьшается и содержание ячеек в единице объема материала.
Исходя из отмеченных положении, приходим, после ряда пробных прикидок, к нижеследующей формуле, характеризующей искомую общую зависимость
Г. = 8,о( *5?т + lj + 7,12 (rf — 0,14)°-8-0,05т, (10)
Где — прирост коэффициента теплопроводности X на каждый процент объемного влагосодержания материала в %•
Как видно из рис. 28, соответствующие этой формуле кривые достаточно удовлетворительно сходятся с результатами испытании.
Формула (10) дает возможность осуществлять практический учет влияния влажности на коэффициент теплопроводности неорганических материалов ячеистого строения при содержании влаги до 15—20% (по объему).
Таким образом, оказывается возможным определять значения коэффициентов теплопроводности указанных выше материалов при любой их влажности (в отмеченном пределе) по следующей формуле:
Где /.„, коэффициент теплопроводности влажного материала їв ккал/м час град; і —определяется по формуле (L'); '•w—определяется. по формуле (10); w влажность материала в % по объему.