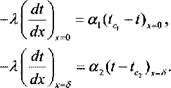Стационарное поле температур тел с источниками тепла
Введём следующие ограничения: тела рассматриваются с
постоянным тепловыделением по объему; на границах тел теплообмен подчиняется закону Ньютона (условия третьего рода); теплопроводность и теплоотдача не зависят от температуры.
Неограниченная пластина.
с) t t
Из уравнения (2.9) при —=- = —- = 0 следует, что
|
(2.47) |
И t
A—j + W = 0, 0<х<5.
dx
|
|
Запишем условия на границах (рис. 2.4 а)
(2.48)
(2.49)
Решение
W,
|
dxydx) А’ dx А |
t = ~ х +C, x + C2. (2.50)
Постоянные интегрирования С/и С2найдём из уравнений (2.48) - (2.49):
|
t(-2 > Н2 |
|
|
X |
|
|
6=2L |
|
t 01 l('l> ui |
|
|
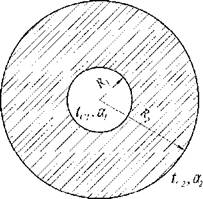
Рис. 2.4. К определению стационарных полей температур тел с
источниками энергии
SHAPE * MERGEFORMAT

Рассмотрим частные случаи
К,=Кг=К’ а,=аг=а,
W5
|
Тогда |
WS
|
С, |
С2 ~ tc г
2Х z L' 2а
Подставим значения С] и С2 в (2.50):
W5,1 х х[1].
TOC o "1-5" h z t = t+ (—+------------ ).
с 2 а X Х5
Последнее выражение преобразуем, введя новую систему координат:
8 т т 5
х-х - X-L; L-—.
|
(x'+Lf 2 L |
|
WL WL t — t —--- 1--- а X |
|
(*'+£)- |
|
(2.51) |
|
EL+m(x.+i)<Lzl2=m+]L(i^x% a X 2L a 2X |
|
WL WL T. r2L-x'-L1 — + — (x'+L)[-------------------- ] a X 2 L |
Найдём максимальную температуру tmax, которая соответствует центру пластины x=L, а х'=0.
|
Неограниченный сплошной цилиндр. Дифференциальное уравнение и граничные условия имеют вид |
|
d2t 1 dt -------------- dx х dx dt |
|
W_, X ' |
|
(2.52) |
|
dt a, 1— (t — t Л dx X |
|
= 0, |
|
dx |
|
1=0 |
|
Представим (2.52) в виде |
|
d, dt. — (x—) dx dx |
|
W |
|
Решение этого уравнения |
|
dt _ Wx C, dx 2X x |
|
dx 2X W 2 ^ • —“ X 4- C, ІПХ4- С. AX 1 2 |
|
-00, ЧТО |
|
Найдём постоянные интегрирования С; и Сг. При х = 0, абсурдно, поэтому полагаем С] = Ои запишем решение в виде |
|
W 2 . х + С-, АХ 2 |
|
Из условий на границе x=L определим Сг. |
|
dt dx |
|
Wx 2Х |
|
WL |
|
с =L |
|
c-L |
|
WL а ґ W т2 _ ч А “--- + X + ^ ( Л — 0. 2Х X АХ |
|
Окончательно температурное поле цилиндра имеет вид |
|
W, т1 г, W т t-t =—(1} - х )н L с АХ 2а |
|
Полный неограниченный цилиндр (рис. 2.4 б). Дифференциальное уравнение для неограниченного цилиндра имеет вид (2.52), его решение было получено выше. |
|
(2.53) |
w
t = Xі + С. Inx + C7
4 1 1 2
На границах x = Rjvlx = R2 теплообмен происходит по закону Ньютона со средами, температуры которых равны t и tc, а коэффициенты
теплообмена - и а2 , Граничные условия имеют вид
|
dt dx |
|
1 |
|
x—R^ |
|
(2.54) |
|
А— dx |
|
«1 (t t. )[ |
|
a2(t - t) |
Используя эти условия, найдём постоянные С/и С2'.
|
1 |
W
|
41 |
С, - —[а, а2 (Г2 - Г,) + у (Я2а, + Д, а2) +
С2 + (/?,2 In Д2 - R; In Д,)- — (а, In Д, + а,/?, In /?2) +
41
WX R R a, t aJ
|
a, V й2 Ді у |
+^f-f)+a'a2 {h'ln Rl ~ ^ ык^+л(-^+;
В = a. a~, ln —3- + 1
Пример. Полый электрический проводник охлаждается водой, текущей в его внутренней полости и естественной конвекцией на наружной поверхности, находящейся в воздухе. Размер проводника Rj = 2 мм, i?2 =3 мм, удельное сопротивление материала />=0,1 Ом мм / м, 1=
15 Вт/мК, сила тока 7=1000 А, аз =1000 Вт/м2К, а2 = Ю Вт/м2 К, ^ _30°С,
^ =20°С.
Требуется определить максимальную температуру проводника.
Решение: Найдём координату х0, соответствующую максимальной температуре
dt
С W 21С
|
dx |
il o=0; Xq = Jt± = о,00298м
х0 21 V W
Поскольку Ri<x0<R2 , то максимальная температура достигается внутри проводника и можно воспользоваться полученными выше формулами (в противном случае максимальная температура наблюдалась бы на одной из поверхностей).
С2 =1304,9; С, =120,5; tmax =543,9°С,
|
при такой высокой температуре следует рассмотреть вопрос кипения воды. Шар с источником энергии. Дифференциальное уравнение имеет вид: |
|
d2t 2 dt W Л ^ ^ _ —_-1--------- __—^ о < х ^ L dx х dx Я |
|
(2.55) |
|
На границе x=L теплообмен происходит по закону Ньютона, поэтому граничное условие имеет вид |
|
-л* dx |
|
('-OL |
|
■ а |
|
x—L |
|
Максимальная температура должна быть в центре шара, что позволяет записать |
|
dt dx |
|
t=0 |
|
Покажем решение приведённой выше системы уравнений. Представим (2.55) в форме |
|
1 d2(xt) W - д |
|
d(xt) dx |
|
Я |
|
Я |
|
х dx |
|
Интегрируя дважды последнее уравнение, получим |
|
d(xt) W х2 _ ,. . W х2 , ^ J — _ ь С,, d(xt)— — dx + Cidx, dx Я 2 1 Я 2 |
|
Wx2 „ С2 1- С, н-------------- 6 Я х |
|
WXі Я 2-3 |
|
+ С[ х + С 2t ■ |
|
tx |
|
где С]И С2 - постоянные интегрирования. Устремим х—>0, тогда t —юо, что физически абсурдно, поэтому |
|
Wx2 6 Я |
|
полагаем С? = 0 и t |
|
+ С,. |
|
На основании условия (2.56) определим Сь |
|
WL WL „ WL2 „ X = a[ hC-r]; ЗЯ ЗЯ 6Я 1 c |
|
dt dx |
|
запишем выражение для искомой температуры: |
TOC o "1-5" h z w w
t-te= №-?)+ L (2.57)
62 3a
Приведём сводку формул для трех тел простейшей формы:
tm~te=—(L ~хг) + — Ц 22 а
W /г2 2ч W т
t - f = — (L-x) +------- L;
цш c 42 } la
W tT2 2ч W T
t “ t — — (X “X ) + — L,
62 Ъа
Во всех случаях температурное поле тела представляется параболическим законом. При а=оо и х=0:
WL2 WL1 WL1
tnn tc~^U’ ^ tc~ 4Л’ *ш *е~ 62'
Найдём среднюю объёмную температуру пластины, цилиндра и шара; по определению
|
{v ~~К V с у У V |
|
(2.58) |
U(t~Odv,
где V и dV - объём и элемент объёма тела.
Ki - 2L-1-1, dVu=dx-l'l, ~L<X<L - Кц = жі} ■ 1, dVц = l/rxdx •1, о < x < і •
Э
V = —77ТЪ ш 3 ’ dVm = 4nx1dx, о <x<L
Подставляя в (2.58) значения разности температур из (2.51), (2.53) и (2.57) и производя интегрирование, получим после простых преобразований выражение для среднеобъемного перегрева
(2-59)
где P=W'V - полная мощность источников в теле; V и S - объём и теплоотдающая поверхность в теле; п - коэффициент, равный для пластины, цилиндра и шара
1 1 з
пп=у я,--’ ”“ = 5' ^2-60^
Формулу (2.59) можно также применять для оценки средней объёмной температуры тел иных конфигураций с распределёнными источниками энергии. Для этого следует все тела разбить на три группы: тела группы шара имеют все три измерения одного порядка; тела группы цилиндра имеют два конечных измерения одного порядка и третье измерение - неограниченно большое (z, «ь «ьъ); тела группы пластины обладают одним измерением конечной величины с двумя другими неограниченно большими измерениями (z, <<z2 » Z3 )• При оценке Э,, для тел указанных групп следует выбирать соответствующие значения п из (2.60) или промежуточные значения этих величин.