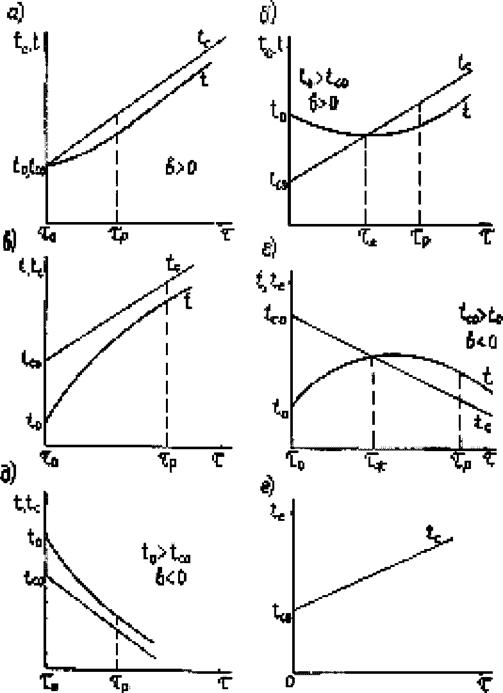
Нагревание или охлаждение тела в среде, температура которой изменяется во времени с постоянной скоростью
Рассмотрим следующий случай (рис. 2.6 е):
tc=b{r-T0) + tc0, Р = Р0= 0. (2.77)
Согласно (2.69) F0 = tc0, F =tc, и из формулы (2.70) следует, что
г
t-tc =(t0 I ещг dr.
После преобразований получим
t-tc=-b_ + (t0-te0+—)e-a (2.78)
mQ m0 ^
Графическое представление разновидностей рассматриваемых режимов дано на рис. 2.6, из которого видно, что возможны случаи пересечения кривых t(r) и tc (г) , однако, такое пересечение может быть только в одной
точке, соответствующей максимуму (рис.2.6 г) или минимуму (рис. 2.6 б). Запишем условие пересечения
t(T.) = tc(r.) (2.79)
и найдём время г», когда происходит пересечение кривых. Из (2.79) и (2.78) следует, что
|
Рис. 2.6. Охлаждение или нагревание тела в среде, температура которой меняется по линейному закону |
тп
Откуда
|
(2.80) |
Т, = г0 + — 1п(1 + ———).
|
тп |
Ытп
Если f0 = ?с0, то пересечение происходит в точке т, =г0 (рис. 2.6 а). При г0 > гс0 и 6>0 точка пересечения соответствует времени т, > г0(рис. 2.6 б). Рассмотрим отдельно случай
tc0>t0b b>0.
Как следует из (2.80), аргумент In будет меньше единицы, и второй член в правой части этого уравнения всегда будет отрицательным, т. е. уравнение имеет решение лишь для г* < т0 . Последнее означает, что пересечение никогда не произойдёт, так как рассматриваются процессы, протекающие
при т>т0, а т„>т0 (рис. 2.6 в). Для Ь<0 и tc0 > t0 выражение ——— >0 и,
Ь/тй
следовательно, г, >т0 , т. е. возможно пересечение кривых t(j) и fc(r)
(рис. 2.6 г). Наконец, для Ь<0 и tcQ <t0 выражение — — < 0, т. е. т, < т0, что
b/m0
означает невозможность пересечения кривых t{z)vi. tc{т) (рис. 2.6 д).
Рассмотрим теперь, как изменяется ход кривой t(r) с течением времени. Со временем второе слагаемое в (2.78), содержащее экспоненту е~тч (*—го) в качестве множителя, становится пренебрежимо малым по сравнению с первым, т. е. разность температур тела и среды стремится стать постоянной
(2-81)
при больших значениях (г-г0). Из рис. 2.6 видно, что с течением времени кривые t(v) и tc{г) становятся практически параллельными. Обозначим
время, начиная с которого с заданной степенью точности можно не учитывать второе слагаемое в (2.78), через туи тепловой режим тела при т>тР назовём регулярным режимом второго рода, а при т < тР - иррегулярным (дорегулярным) режимом. Слово регулярный (regular) дословно означает «правильный», «закономерный». Здесь оно употребляется в смысле «упорядоченный» и в рассматриваемом конкретном случае означает, что спустя некоторое время начальное температурное состояние перестаёт влиять на температурное поле тела. Иногда такой режим называют «квазистационарным». Из сопоставления общего выражения для температурного поля тела (2.78) с выражением (2.81), а также анализа рисунков 2.6 следует, что для всех случаев соотношений t0 и tc0 при т>тР разность температур (tP-tc) изменяется по одинаковому закону (2.81). В развёрнутом виде уравнение (2.81) примет вид
|
b |
|
b< 0 |
|
(2.82) |
|
tp(T)^tc0+b(T-T0) |
Выражение (2.78) является точным решением задачи, а (2.82) — приближенным. Для некоторых технических задач часто бывает удобно использовать такого рода приближенные выражения.
В заключение заметим, что процесс нагревания или охлаждения тела в среде, температура которой изменяется во времени с постоянной скоростью, в чистом виде встречается редко, а для своего осуществления требует применения специальных средств регулирования. Однако некоторые явления, протекающие в естественных или лабораторных условиях, можно в первом приближении свести к рассмотренному здесь процессу или к их совокупности. Например, охлаждение метеозонда при его подъёме можно с довольно грубым приближением описать с помощью приведённых выше уравнений.