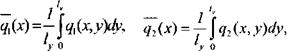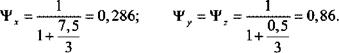Тепломассообмен

Критерии неравномерности поля температур в теле

Критерии 4'z,4'/,4'1,4'2, определенные выражениям (2.98), (2.106),

(2.109), характеризуют неравномерность температурного поля в поперечном сечении тела. Можно попытаться найти точное значение для этих критериев. Для этого необходимо иметь точные аналитические выражения температурного поля и произвести с ними операции, указанные формулами (2.98), (2.106), (2.109). В общем случае эти критерии будут изменяться с координатами, что затруднит интегрирование дифференциальных уравнений (2.99), (2.107), (2.109). Для случая

4'z=4'j;=4'1=4'2= 1 (стержни и пластины) интегрирование этих уравнений,

как будет показано ниже, не представляет труда и приводит к сравнительно простым выражениям. Однако для того, чтобы знать

величину критерия ¥ в каждом конкретном случае и быть уверенным в возможности свести задачу к пластине или к стержню, необходимо получить хотя бы приближенные зависимости для оценки *Р. Предположим, что критерий ¥ не зависит от координат; численные значения этого критерия для многомерного и одномерного температурного поля незначительно отличаются друг от друга.

Эти два предположения существенно упрощают задачу отыскания аналитического выражения для *Р.

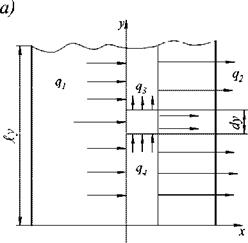
Изложим один из путей решения этой задачи. Рассмотрим процессы переноса тепла в твёрдом теле и покажем физический смысл приведённых выше операции осреднения. На рис. 2.9, а показан элементарный объём dxdy, в левую грань которого входит удельный поток q{{x, y),а из правой - выходит q2{x, y), с верхней и нижней граней рассеиваются удельные потоки Чъ(х, у) и q4(x, y) . Обычно при составлении уравнения баланса энергии рассматриваем малый объём dxdy и рассчитываем ту часть потока QT, которая за счёт теплопроводности пришла (или ушла) в данный объём

Qt = (?: - <h)dy + (Уі - q4)dx,

а затем, учитывая другие источники или стоки энергии Q, на основе закона сохранения энергии QT=Q. Если теперь произвести операцию осреднения по одной из осей, например у,

а вместо локальных потоков чъ(х, у) и q4(x, y) будем рассматривать их частные значения при у = 0 и у = I., т. е.

Тогда пришедший (или ушедший) в элемент lydx поток выразится в виде

Qt = Яі (*) - Яі 0ЭД. + [Яз (*> h) - я a (*,0)]<fr.

Другие источники или стоки для объёма lydx дадут поток Q = JQdy,

О

сохранения примет вид QT = Q.

б)

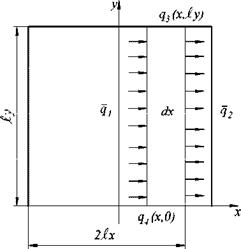
Рис. 2.9. Анализ физического смысла операций осреднения

Из этих рассуждений следует, что при осреднении по одной из осей (например, у), разность между вошедшим и вышедшим из объёма потоком, во-первых, рассматривается для осредненных значений потоков (рис. 2.9 б), а во-вторых, эта разность потоков может быть представлена в виде внутреннего (в данном элементе ljx ) источника энергии постоянной

мощности. Следовательно, для оценки критерия неравномерности температурного поля в каком-либо направлении возможно рассмотреть простейшую задачу об одномерном температурном поле тела с постоянным источником энергии.

Заметим, что здесь идёт речь не о точном вычислении критериев неравномерности поля, а только об их оценке.

Например, для неограниченной пластины толщиной 21х с постоянным источником энергии и условиями третьего рода на границах х = ~1х и х = 1х на основании (2.15) имеем

Найдём отношение средних на поверхности (х = 1х) и по объёму перегревов Ss и 9V.

Из приведённого выражения следует, что

Отношение температуры &s и &г по определению является критерием неравномерности поля температур. Для пластины равно

(2.112)

Температурное поле неограниченного цилиндра с источником тепла описывается выражением (2.53). Определяя температуры &s и Эу для

цилиндра:

и беря их отношение, найдём критерий Ч'ц:

1 А Hi

4

Предположим теперь, что критерии ¥ не зависят от координат, и численные значения этих критериев для одномерного и многомерного полей температур незначительно отличаются друг от друга. Специально проведённый для многочисленных конкретных случаев анализ показал, что для стационарного режима сделанные допущения, а также способ оценки критерия ¥ по формулам (2.112) и (2.113) для простейших тел с равномерно-распределёнными источниками тепла приводят к удовлетворительным результатам. Зависимость (2.112) позволяет оценить критерий и 1Т'у для приведённых выше случаев.

Эти формулы позволяют решить вопрос о возможности использовать уравнения (2.99), (2.107), (2.109) для нахождения температурного поля стержня и пластины.

Пример. Параллелепипед, размеры граней которого равны 21 х = 20 см, 21 = 21 z = 8 см, обменивается теплом с окружающей средой по закону

Ньютона, коэффициенты теплообмена на границах параллелепипеда ах= 15 Вт, Ом1 - К), ay=az=5 Вт!(м2-К), Коэффициенты теплопроводности

параллелепипеда в направлениях осей х, у, z: Ах = 0,2

Вт /(м-К), AX=AZ = 0,4 Вт/(м-К). Оценить возможность рассматривать температурное поле такого тела по формулам для стержня.

Решение. Найдём значение критериев Bi и вычислим по формулам (2.114) критерии, ч, у, :

Следовательно, по осям у и z отношение среднего поверхностного перегрева к среднеобъёмному близко к единице, т. е. градиент температур в этих направлениях мал. В направлении оси х существенна неравномерность поля температур. В данном случае параллелепипед можно рассматривать как стержень.

Если в дифференциальных уравнениях (2.99), (2.107), (2.109) полагать ¥ не равным единице, а подставлять их значения, вычисленные по формулам (2.113), (2.114), получим более точные выражения для температурного поля стержней и пластин. Естественно, такие поправки следует вводить для значений ¥ , близких к единице, например,

> 0,8 . Для < 0,8 , по-видимому, следует искать точное решение задачи.