Второе начало термодинамики и его применение к физико-химическим процессам
Второе начало термодинамики, предсказанное еще М. В. Ломоносовым, было окончательно установлено в середине XIX в. Клаузиусом и Гельмгольцем (1850—1851). Оно позволяет определить возникновения самопроизвольно протекающих процессов в термодинамических системах и формулируется так: при самопроизвольном переходе теплоты от нагретого тела к холодному, часть тепловой энергии может быть переведена в работу.
Формулировка второго начала
термодинамики
|
|
|
Pi Рг Pi Рз |
|
и |
|
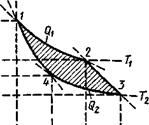
Рис. 8.2. Цикл Карно в р-и-коорди - натах |
Исследование идеального цикла тепловой машины. С. Карно позволило установить условия для получения работы за счет тепловой энергии и тем самым сформулировать второе начало термодинамики. Цикл Карно совершается между двумя изотермами и двумя адиабатами (рис. 8.2), причем предполагается полная обратимость процессов. Подсчитывая изменения параметров состояния, значения работы и теплоты при отдельных процессах, можно показать, что в результате проведенного цикла получили работу, равную площади 1,2,3,4,1, очерченной циклом, в свою очередь равную разности взятой Q! (на участке 1—2) и отданной Q2 (на участке 3—4) теплоты (Qi — Q2). Математически это можно выразить уравнением:
Аа= Qi — Q2 = /?[1п(о2/
/оі)](Г, - Г2). (8.15)
|
V. |
Введем понятие термического коэффициента полезного действия цикла, отнеся полученную работу к теплоте, взятой из среды с температурой Ті:
Пи— (Q і Qi)/Q = Ац/Q і =
= (Г, - 7-2)/Г,. (8.16)
Следовательно, процесс получения работы сопровождается переносом теплоты от более нагретого тела (Гі) к менее нагретому (Тг). Поэтому perpetuum mobile 11 рода невозможен, так как он должен создавать работу только в результате понижения температуры окружающего пространства при E = const. Следовательно, коэффициент полезного действия такого устройства будет равен нулю
Таким образом, второй закон термодинамики формулируется следующим образом нельзя построить периодически действующую машину, которая только совершала бы работу и охлаждала резервуар теплоты в работу можно превратить лишь часть теплоты, самопроизвольно переходящей от нагретого тела к холодному
Если провести цикл Карно в обратном направлении, то теплота будет переходить от холодного тела к нагретому в результате затраты внешней энергии (холодильный цикл).
Теплота не может самопроизвольно переходить от холодного тела к нагретому
Полученные соотношения попробуем применить к молекулярным процессам, происходящим в термодинамических системах
Рассмотрим цикл Карно между двумя бесконечно близкими изотермами В этом случае термический коэффициент полезного действия
i) = dQ/Q = dT/T=dA/Q (8.17)
такого цикла будет стремиться к нулю. Из этого выражения можно определить теплоту Q, сообщенную в систему при температуре Т:
Q = TdA/dT. (8.18)
Полученное выражение справедливо для обратимых процессов. Представим себе процесс обратимого испарения (рис 8 3, а), при котором жидкость, переходя в пар, будет производить работу
|
S) |
|
а) |
|
T/7=C0nstr №1111111 |
|
|
|
т = const |
расширения, перемещая поршень, нагруженный давлением насыщенного пара жидкости, вверх при постоянной температуре Т. Если бы цилиндр не был закрыт поршнем, то процесс испарения совершался бы необратимо, так как молекулы пара диффундировали бы в окружающее пространство (рис. 8.3, б).
|
Л Ни, |
|
й н„ |
|
Рис 8 3 Обратимый(а) и необратимый (б) процессы испарения |
Работа обратимого процесса испарения может быть определена следующим образом.
А = p(vn— о ж).
Так как давление насыщенного пара — функция температуры, то можно записать:
dA/dT=(dp/dT)(v„—vx)
(изменением удельных объемов жидкости и пара от температуры пренебрегаем).
Подставляя полученное выражение в (8 18), одновременно заменяя Q на теплоту испарения АН ясп получим
AH„cn=T(dp/dT)(v„— о ж). (8.19)
Это уравнение (8.19) носит название уравнения Клаузиуса — Клапейрона и имеет большое значение для изучения фазовых превращений — плавления, возгонки (сублимации), полиморфных превращений в твердом состоянии
В общем виде это уравнение можно записать так:
AHar=T(dp/dT)Avnv. (8.20)
Уравнение Клаузиуса — Клапейрона для испарения можно решить с некоторыми допущениями - 1) отбросить за малостью объем жидкости по сравнению с объемом пара, 2) считать приближенно, что насыщенный пар подчиняется уравнению состояния газа (v — RT/p). Тогда можно записать:
АН исп= T{dp /dT)RT/p=RT2d(np)/dT. (821)
Уравнение (8 21) можно решить с различными степенями приближения
1. Полагаем ДЯИСП= const, тогда
np=-AH„J(RT) + C (8 22)
2. Задаем в виде температурного ряда значение А#ис„:
АНЯСП=АН0 + аТ + ЬТ2.
После интегрирования получаем следующее уравнение:
1пр= - AH0/(RT) + (a/R)nT + (b/R)T+ С. (8.23)
Постоянную интегрирования обычно определяют по экспериментальным данным, а само уравнение преобразуют после перехода к десятичным логарифмам в следующее:
gp=-A/T + BlgT + CT + D. (8.24)
В эту форму уравнения хорошо укладываются зависимости
давления насыщенного пара от температуры для очень многих веществ. Некоторые данные для расчета приведены в табл. 8 2.
При высокотемпературных процессах сварки давление насыщенного пара свариваемого металла над ванной может быть весьма значительным. По данным табл. 8.2, кроме давления насыщенного пара, можно найти температуру кипения или разность энтальпии при испарении.
|
Таблица 8.2. Данные для расчета давления насыщенного пара для некоторых металлов
|
|
Примечание. Для А1ж температурный интервал 1200...2800 К, Мо»— 2900...35 ООО К; W, = —2000...3500 К, для остальных веществ — ТПЛ...ГКЯП. |
Например, используя данные табл. 8.2 и уравнение (8.24), можно определить температуры кипения хрома при нормальном давлении (1,013* 105 Па) и в вакууме с остаточным давлением 1,33-10_4Па (10-6мм рт. ст.), которые равны соответственно 2707,6 и 1069 К.
Разность энтальпий испарения меди можно определить как функцию температуры, используя данные табл. 8.2:
А//„Сп=337 800 — 24,362 Т, Дж/моль.
ЭНТРОПИЯ КАК ТЕРМОДИНАМИЧЕСКАЯ ФУНКЦИЯ
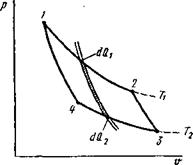
Рассмотрим цикл Карно между двумя бесконечно близкими адиабатами (рис. 8.4). Работа этого элементарного цикла будет тоже бесконечно мала, но термический коэффициент полезного действия может быть достаточно высоким:
т]=(dQi-dQ2)/ rfQi =(7'1 — TaVr,. (8.25)
Разделим дроби почленно на знаменатель и получим -dQ2/dQi = l-T2/Tu Вычитая из единицы обе части равенства, получаем
dQ2/dQi — T2/T или dQ2/T2-dQ/Tv = 0. (8.26)
Отсюда можно записать для любого обратимого цикла:
Следовательно, в любом обратимо проведенном цикле все изменения величины dQ/T в конечном итоге равны нулю.
|
Рис. 8.4. Цикл Карно между бесконечно близкими адиабатами |
По теореме Грина, представляющей собой частный случай теоремы Остроградского, можно заменить подынтегральное выражение полным дифференциалом другой функции от тех же параметров, если интеграл по контуру обращается в 0.
|
(8.28) |
Клаузиус ввел понятие новой функции от тех же параметров (р, v, Т), обозначил ее s и назвал энтропией, исходя из условия:
ds — dQ/T или dQ=Tds.
Используя эту функцию, можно записать уравнение (8.28) в следующем виде:
§ds=0, (8.29)
т. е. при проведении обратимого цикла изменение энтропии в системе равно нулю (результат распространяется на все случаи обратимых циклов). Если же цикл необратим, то работа будет меньше, чем в обратимом, проведенном в тех же условиях:
Л =(rfQ, - rfQ,)/dQ, <(Г, - Т2)/Ти (8.30)
Следовательно, после аналогичных предыдущему преобразований придем к другому результату:
|
(8.31) |
§ dQ/T>0 §dQ/T = 0,
необр обр
т. е. при проведении необратимого цикла изменение энтропии будет больше нуля или энтропия системы увеличивается.
Рост энтропии указывает наличие в системе необратимых процессов; s стремится к максимальному значению при равновесии, т. е. когда все необратимые процессы будут закончены. Можно из определения энтропии записать:
ds = dQ/T = dU/T - f pdv/T или при условии t/ = const и у = const
ds—► 0; S—►Smas
т. e. стремление энтропии к максимальному значению (условия экстремума ds>0) указывает на приближение системы к равновесию.
ЗАВИСИМОСТЬ ЭНТРОПИИ ОТ ТЕМПЕРАТУРЫ, ФАЗОВОГО СОСТОЯНИЯ И КОНЦЕНТРАЦИИ
Энтропия — весьма информативная функция, которая зависит ие только от параметров процесса (р, v, Т), но и от свойств систем, участвующих в этом процессе.
Зависимость энтропии от температуры легче всего определить для моля идеального газа. По условию,
ds = dQ/T.
Заменяем dQ, используя уравнение первого начала термодинамики:
ds = dU/T-^-pdv/Т.
Для идеального газа dU—cvdT, а заменяя p = RT/v по уравнению состояния Клапейрона — Менделеева, получаем
ds = cvdT/Т4-Rdv/v.
|
(8.32) |
После интегрирования в пределах от абсолютного нуля до Т получаем
s г= so + с» In 7" +Ліпи,
где St— энтропия моля идеального газа при температуре Т, sо — энтропийная постоянная (или s—О при О К); cv — молярная теплоемкость газа при y=const; v — молярный объем газа.
Из уравнения (8.32) видно, что энтропия представляет собой функцию температуры, давления (через молярный объем), ио она также зависит от величины с„. Теплоемкость идеального газа зависит от строения молекул: для одноатомного газа с„ = = (3/2)R, а для двухатомного газа из-за увеличения степеней свободы движения она будет равна cv = (5/2)R. Таким образом, даже в самом простейшем случае энтропия отображает строение частиц, составляющих систему. Для реальных веществ, у которых прн изменении температуры существуют фазовые превращения, энтропия должна изменяться при каждом превращении. Ее изменение можно определить по формуле
|
(8.33) |
As = AHn?/T „р,
где ЛЯпр—изменение энтальпии при изменении фазового состояния; Т„р— температура превращения.
Расчетное уравнение для энтропии реальных веществ становится весьма сложным, так как оио должно учитывать изменение фазовых состояний и температурные зависимости теплоемкости, меняющиеся для каждого фазового состояния системы. В общем виде его можно представить уравнением
|
|
где ср— молярные теплоемкости вещества в данном фазовом состоянии; ЛНпр— разности энтальпий фазовых превращений.
Кроме температуры, давления и фазового состояния энтропия очень сильно зависит от концентрации вещества в данной системе. Концентрация в смеси веществ или в растворах в термодинамике определяется через мольные доли, определяемые отношением числа молей данного вещества к сумме молей всех веществ, участвующих в данной системе:
№ = л./2л„ (8.35)
где п, — число молей данного компонента; N, — его мольная доля.
Рассмотрим процесс смешения двух идеальных газов, не реагирующих между собой. Пусть в двух частях объема, разделенного перегородкой А, находится П молей первого И ГІ2 молей второго газа (рис. 8.5, а).
Если удалить перегородку А (рис. 8.5, б), то произойдет перемешивание газов в результате диффузии и иа каждый моль газа любого компонента будет приходиться часть общего объема смеси Ко:
Vo = vZn,; vl = v'Ln,/nl Следовательно, энтропия любого моля компонента і в смеси
Sr=Sg + Ct,.ln 7 + /? In г?2 П,/п,.
Преобразуем выражение s't следующим образом:
sf=(so + cJn Т + /?1пи) — RnNt,
|
Рис 8 5 Объем с двумя і азами до (а) и после (б) их смешения |
где N, = щ/Zn, — мольная доля данного вещества в смеси (уменьшаемое — тепловая, вычитаемое — концентрационная части).
Полученное выражение определяет очень важное понятие, а именно рассеяние или диссипацию вещества, так как если Ni -*■ 0, то энтропия стремится к бесконечности, т. е. выделение вещества в чистом виде из данной смеси будет возможным лишь при очень большой затрате энергии. Это и создает громадные трудности при выделении в чистом виде «рассеянных» металлов, таких, как бериллий, иттрий и др.
|
р, Т - const
|
Большое количество факторов, влияющих на значение энтропии, вызывает необходимость стандартизации табличных значений энтропии для различных веществ. Табулируются значения энтропий чистых веществ в Дж-моль_1-К-1, измеренные при стандартных условиях (7=298,15 К; р=1,013-105 Па). Значения энтропий ряда веществ приведены в табл. 8.3.
Если исследуется процесс при температурах, отличных от стандартных (7=298,15 К), то значения энтропий, взятые из таблиц для стандартных условий, надо пересчитывать по уравнению
5°7=^98,15+2 5 -^Д+2-^. (8.36)
298,15 "Р
Для веществ газообразных, не испытывающих фазовых превращений,
г
„о о і С c„dT
5 7=5 298,15+ J —+—•
298.15
Для многих веществ значения энтропий просчитаны при различных температурах и в справочной литературе можно найти таблицы (s°t—s 298.15), что значительно упрощает расчеты. Учет концентраций для газовых смесей следует вести по уравнению
s'r=s°—Д1пМ. (8.37)
Для других систем (растворы) надо учитывать активные концентрации и коэффициенты активности.
Пример 3. кассовая доля углерода в стали 35 составляет 0,35%. Определить энтропию моля углерода в стали 35, считая коэффициент активности углерода в стали за единицу.
S298.i5=s° — R 1пМ; «с = 5,74 кДж/(моль - К);
0.35/12
0,35/12 + 99,65/56 ~ ; 1п^с = 4,135;
|
Таблица 8.3. Значения стандартных энтропий So для некоторых веществ sc =5,74+ 8,31 -4,135 = 40,1 Дж/(моль-К). Энтропия углерода возросла в ~7 раз.
|