Тепловые процессы при электрошлаковой сварке
Одна из наиболее характерных особенностей тепловых процессов при электрошлаковой сварке — значительная распределенность источника теплоты. Основной металл подогревается шлаком на довольно значительной длине, составляющей около
30.. .70 мм. На заключительной стадии нагрева кромки основного металла разогреваются активной зоной шлаковой ванны и опускающимся расплавленным электродным металлом, в результате чего образуется металлическая ванна шириной, равной ширине шва 2Ьпр (рис. 7.21, а).
В простейших инженерных схемах расчета воспроизвести сложную пространственную форму выделения теплоты при электрошлаковой сварке не представляется возможным. Хорошо отвечает фактическому распределению температур и форме проплавления следующая расчетная схема источника теплоты (рис. 7.21,6): в сплошной пластине без сварочного зазора f движутся три (равномерных по толщине металла) источника теплоты в виде линий AC, BD, расстояние между которыми равно ' и AtBi. Мощность источника на линии АВ соответствует
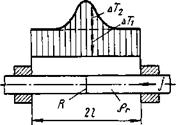
Рис. 7.21. Схема нагрева металла прн электрошлаковой сварке:
а — схема процесса; б — схема движения шлаковых qm и металлического qu источников теплоты
количеству теплоты, приносимому расплавленным электродным металлом в секунду:
Ч*=фрк™ (7-48)
где v — скорость сварки; / и 6 — зазор и толщина металла; р — плотность; hnil — теплосодержание в единице массы металла, если его определять от Ти до температуры шлаковой ванны в ее активной зоне.
Мощность qm двух источников АС и BD равна разности между всей эффективной мощностью источника q и мощностью так называемого металлического источника qK:
ЯШ=Я~Я«- (7-49)
Теплота, выделяемая по линиям АС и BD и распространяющаяся влево от АС и вправо от BD, соответствует подогреву кромок пластин шлаковой ванной. Теплота, распространяющаяся вправо от АС и влево от BD, вследствие ухода источников вперед в основном создает тепловой поток через сечение АВ, что соответствует подогреву металла ванны со стороны шлака, который имеет более высокую температуру, чем расплавленный металл в ванне. Линейная интенсивность мощности равна <?м/(26пр) у металлического и qul/(2hUI) у шлакового источников теплоты. Такой нагрев предопределяет характер распределения температур в пластинах. Изотермы подходят к свариваемым кромкам
под некоторым углом, отличающимся от 90° (рис. 7.22), нагрев
кромок происходит задолго до их плавления. Приращение температуры в любой точке может быть подсчитано с использованием выражения (6.26) путем его интегрирования с изменением х
|
Рис. 7.22. Температурное поле предельного состояния при электрошлаковой сварке, рассчитанное по схеме двух шлаковых и одного металлического источников теплоты (б = 10 см, { = 2 см, Лш = 6 см, <7Ш = 10 кВт) |
в пределах /гш, а у в пределах от — Ьпр до + Ьпр при интенсивностях металлического и шлакового источников, указанных выше:
4r=^r't'V.(^ VF+?)*,+
пр {у—Ь пр)
+7І7, S, Г""а" f +
ш (*—Ащ)
+ 4 -^л/х* + (у+ь„ру] } dx, (7.50)
где р = V1 +46а/ра; 6 = 2а/(ср8); х, у—координаты точки, в которой определяется приращение температуры.
Начало движущейся системы координат для уравнения (7.50) находится в точке О (см. рис. 7.21,6). Так как заранее до расчета значение 6пр неизвестно, то определение приращения температуры по формуле (7.50) может выполняться двояко — в зависимости от расположения точки и требуемой точности. Для точек, расположенных вдалеке от линии сплавления, с максимальным приращением температуры до 700...800 К можно считать bnp — f/2, что условно соответствует минимальной глубине проплавления. При необходимости определения термических циклов вблизи линии сплавления или самой глубины проплавления вначале-нужно найти 6пр. Для этого необходимо в (7.50) про - варьировать значения 6пр, положив в пределах интегрирования первого интеграла, а также в подынтегральном выражении второго интеграла у = Ьпр, а АТтах=Тпл—TV Это условие означает, что берется такое максимальное значение ЛіВі = 26пр, при котором еще достигается приращение температуры, обеспечивающее температуру плавления металла в точке с координатой у=Ьпр. После того как определено 6пр, расчет приращения температур можно проводить для любых точек.
Следует обратить внимание на то, что при электрошлаковой сварке даже без подогрева металла можно обеспечить весьма малые скорости охлаждения, что важно, например, при сварке легированных и, в частности, инструментальных сталей. Этого можно достичь увеличением мощности металлического источника теплоты путем увеличения сварочного зазора f до нескольких десятков сантиметров.
Несмотря на то что при электрошлаковой сварке безразмерный критерий теплоотдачи Р = у/1 4-4ba/v2 может быть близким к единице, его роль может оказаться существенной в образовании неравномерности температуры по толщине АТ& при больших значениях б.
При распространении теплоты в пластине от мгновенного линейного источника [см. формулу (6.6)] поверхностная теплоотдача учитывалась путем введения сомножителя е~ь‘, который показывает уменьшение приращения температуры в среднем, не отражая неравномерности по толщине б. Неравномерность температуры по толщине пластины АТ& при распространении теплоты от мгновенного линейного источника теплоты может быть определена по формуле
АТ* = -Атге-Г,/{ШЩЬТ) =
4яШ '
_ Q 2simn(l —cosft;) c — „Uat/l? (7.51)
4nX6t ^ ^ t|i + sin ті і cosft< ’
где ri—корни уравнения T)c27,/(a6) = ctgT)b
Функция Ф(АТ) зависит от параметра аб/(2Х). Для случая электрошлаковой сварки значения аб/(2Х) обычно находятся в пределах от 0,2 до 1,0.
Приближенно функцию Ф(АГ) в интервале аб/(2Х) = 0,2... 1,0 можно представить суммой заменяющих функций
об 4 at І аб 4at
ф(ДГ)==0,5—е“'*г"*г'—0,164-25-е'- ' ~ ' г-
4 ' 2Х 2Х
|
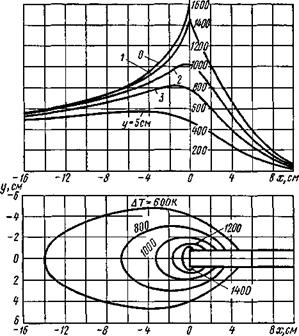
Рис. 7.23. Распределение приращений температур при электрошлаковой сварке плит (q/v = 2400 Вт/см, v = 0,0167 см/с) |
|
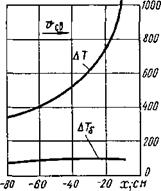
Рнс. 7.24. Распределение приращений температуры по длине свариваемых стержней в процессе их нагрева током |
— 0,336-^-е ^20'3 10,12^'тг‘. (7.52)
2.К
Суммируя разности температур от бесчисленного множества мгновенных линейных источников теплоты (см. п. 6.2), находим
ё к«г^+і1г ~
-0,[64-|-фл/^+-^5,9-2,22-1)] -
-0,336-1-4 'ЛІ ^-+т(20-3-“’•|тг)1 1 • <7'53>
На рис. 7.23 в качестве примера показано распределение приращения средней температуры на оси шва АТ и распределение разности температур AТ&, вычисленное по уравнению (7.53) для 6=70 см, у= 0.