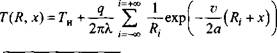Температурное поле предельного состояния в плоском слое
Распределение температур в плоском слое при действии на его поверхности подвижного точечного источника может быть рассчитано с использованием метода отражения. Действительный точечный источник принимают перемещающимся по поверхности
|
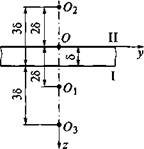
Рис. 6.12. Схема введения фиктивных источников для расчета температур в плоском слое |
полубесконечного тела (рис. 6.12). Отражение потока теплоты, создаваемого источником О, от границы I учитывают введением фиктивного источника 0, симметричного источнику О относительно границы I, т. е. на расстоянии 25 от источника О, действующего на границе II. В свою очередь, граница II для источника 0 будет учтена, если ввести фиктивный источник 02, удаленный от границы II на расстояние 25. Для этого источника необходимо учесть границу I и т. д. В результате таких манипуляций формируется симметричная относительно границы I система бесконечного числа точечных источников, расположенных на оси Oz, причем каждый последующий источник удален от предыдущего на расстояние 25. Такая закономерность расположения источников легко формализуется, что позволяет записать выражение для квазистационарного температурного поля в плоском слое в виде суперпозиции полей предельного состояния всех источников:
|
|
х +у + (z-2/5) - длина радиус-вектора рассматри
ваемой точки А в подвижной системе координат, связанной с /-м источником теплоты; х - абсцисса точки А в подвижной системе координат, і - целые числа от - оо до +оо, і = 0 соответствует реальному источнику О.
Следует отметить, что по мере удаления фиктивных источников
от реального (с увеличением Л/), их вклад в приращение температуры стремительно уменьшается, поэтому для инженерных расчетов можно ограничиться учетом лишь нескольких отражений.
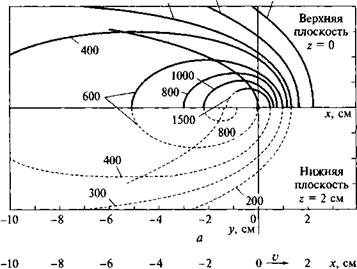
Характер температурного поля в плоском слое (рис. 6.13) позволяет выделить в нем три зоны. В зоне, прилегающей к источнику теплоты, распределение температуры мало отличается от такового в полубесконечном теле (см. рис. 6.11). В зоне, удаленной от
|
300 200 100
|
|
1000 1500 800 -4 -2 0 / 2 У, см |
|
-III- |
||||
|
- |
||||
|
/ |
||||
|
—Jr |
І------- |
|||
|
200 400 600 , „К1 Z, см |
600 400 |
200 |
|
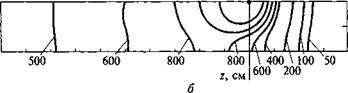
в Рис, 6.13. Температурное поле предельного состояния при наплавке на стальной лист толщиной 8 = 2 см {q = 4 кВт, v = 0,1 см/с, X = = 0,4 Вт/(см • К), а = 0,1 см2/с): а - изотермы и кривые максимальных приращений температур на верхней (z = 0) и нижней (z = 5) поверхностях; б - изотермы в продольной плоскости хOz; в - изотермы и нормальные к ним линии теплового потока в поперечной плоскости yOz |
|
АТ, К |
|
|
|
1600 |
IALx = o |
|
1200 |
і і і |
|
800 |
и 12 |
|
400 |
J/1/ |
|
0 |
х =-12 см і _ і і і _ і |
|
-4 |
|
У, см |
|
О х, см |
|
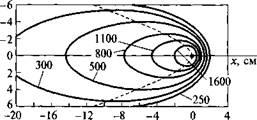
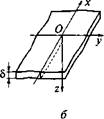
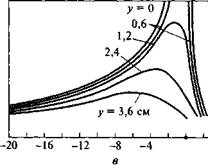
Рис. 6.14. Температурное поле предельного состояния при движении линейного источника в бесконечной пластине толщиной 5 = 1 см (q = 4 кВт, v = 0,1 см/с, к = 0,4 Вт/(см • К), а = 0,1 см2/с, b = 2,8 • 10~3 с-1): я - изотермы на поверхности пластины (штриховая линия разделяет область нагрева и область остывания); б - схема расположения координатных осей; в - распределение приращений температуры в сечениях, параллельных оси Ох г - распределение приращений температуры в сечениях, параллельных оси Оу |
|
|
источника на расстояние более 45, температура по толщине практически выравнена, и распределение ее близко к температурному полю пластины (рис. 6.14). Между этими зонами располагается переходная зона. Соотношение между размерами зон может изменяться в зависимости от параметров источника теплоты, толщины плоского слоя и теплофизических свойств материала.