Температурное поле предельного состояния в массивном теле
|
|
Температурное поле предельного состояния при нагреве поверхности полубесконечного тела подвижным точечным источником постоянной мощности можно получить из выражения (6.19), полагая t = оо. После выполнения ряда математических преобразований получаем следующее выражение для квазистационарного температурного поля:
(6.24)
|
|
|
где |
длина радиус-вектора рассматриваемой
точки А полубесконечного тела в подвижной системе координат; х - абсцисса точки А в подвижной системе координат. Отсутствие переменной ґ, связанной со временем протекания процесса, в выражении (6.24) означает, что предельное состояние достигнуто. Частным случаем выражения (6.24) при v = 0 является выражение (6.7) для температурного поля предельного состояния неподвижного источника.
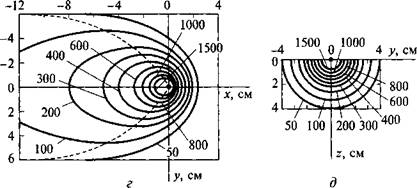
Вид квазистационарного температурного поля подвижного точечного источника теплоты на поверхности полубесконечного тела представлен на рис. 6.11. Изотермические поверхности являются поверхностями вращения относительно оси Ох. Изотермы в плоскости хОу являются замкнутыми кривыми, сгущенными впереди источника и растянутыми позади него. Чем быстрее движется
|
|
|
Рис. 6.11. Температурное поле предельного состояния при движении точечного источника теплоты по поверхности полубесконечного тела (<? = 4 кВт, v = 0,1 см/с, X = 0,4 Вт/(см • К), а = 0,1 см2/с): а - схема расположения координатных осей; б - распределение приращений температуры по прямым, параллельным оси Ох и расположенным на поверхности массивного тела; в - распределение приращений температуры по прямым, параллельным оси Оу и лежащим в плоскости xOz г - изотермы на плоскости хОу (штриховая линия разделяет область нагрева и область остывания); д - изотермы в поперечной плоскости yOz, проходящей через центр источника |
источник, тем более вытянуты изотермические кривые. Изотермы низких температур, соответствующие большим расстояниям R от источника, более вытянуты, чем изотермы высоких температур.