Проводимость твердых тел, жидкостей и газов
ВИДЫ ПРОВОДИМОСТИ
Электрическим током принято называть упорядоченное движение электрически заряженных частиц. В зависимости от состояния и состава вещества его электрическая проводимость может быть электронной (в металлах), электронно-дырочной (в полупроводниках), электронно-ионной (в газах) и ионной (в электролитах).
Внутренняя энергия системы есть сумма всей кинетической и потенциальной энергии частиц. Жидкостям и аморфным телам свойствен лишь ближний порядок, а газы имеют беспорядочное расположение частиц при максимальной внутренней энергии системы. Состояние вещества зависит от температуры Т и значения сил межмолекулярного взаимодействия. Энергия теплового движения или так называемая энергетическая температура частиц равна kT. При высоких температурах значение kT превосходит энергию взаимодействия молекул и вещество может быть только газом. Напротив, в кристалле частицы связаны сильно и энергия взаимодействия много больше kT.
Здесь
k — 1/11 600 эВ/К = 1,38- 10 23 Дж/К — постоянная Больцмана.
Уровни энергии, которыми может обладать электрон в кристалле, определяются принципом Паули, который гласит, что в атоме в одном из любых квантовых состояний может находиться не более двух электронов (с противоположными спинами).
|
КТ |
Распределение электронов проводимости в твердом теле подчиняется статистике Ферми — Дирака (рис. 2.1). С повышением температуры тепловую энергию воспринимают только внешние
валентные электроны, переходящие на еще более высокие энергетические уровни, которые у металлов обычно свободны. Уровень или граница Ферми Wf определяется концентрацией электронов, т. е. зависит
|
п - j J і iww і ІІЦ в 1 M твердого тела ОКОЛО w, — граница Ферми |
1023.. .1029, что характерно для металлов, Wj составляет около
|
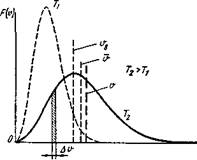
Рис. 2.2. Распределение частиц газа по скоростям согласно Максвеллу — Больцману: |
8.. .10 эВ.
Когда энергия частиц w =
= kT велика по сравнению с Wj, распределение Ферми приближается к максвелловскому, описывающему «классические» частицы в газе (рис. 2.2). Классическое распределение наблю - дается, когда п мало или Т велико.
|
F(v) — число частиц со скоростью v - f - Ди, и, vB и v — средняя квадратичная, наиболее вероятная н средняя арифметическая скорости |
Энергетические уровни электронов в твердом теле объединены в серии и образуют энергетические зоны. Число расщепленных уровней в каждой зоне равно числу атомов, объединенных в кристалл. Установлено наличие трех зон: нижняя зона валентных сзязей; запрещенная зона; зона проводимости.
В зависимости от концентрации свободных носителей, которая связана со способом взаимодействия атомов в решетке, изменяется значение энергетического зазора между валентной зоной и зоной проводимости. Соответственно меняется характер электропроводимости кристаллов (рис. 2.3), которые в связи с этим можно разделить на три класса: проводники (металлы), полупроводники и изоляторы (диэлектрики).
В металлах валентная зона занята не полностью (заштрихованная область на рис. 2.3, а) или занята полностью, но перекрывается со следующей свободной зоной (рис. 2.3, б).
В полупроводниках и диэлектриках валентная зона целиком
|
|
|
Зона прободимости 777. |
|
У/ оимипишии / Ш, жШ |
|
к) w- |
|
г) ш |
|
/7/7/7, 'алентная |
|
Аш<2эВ |
|
7777777777777, 7 Валентная, |
|
х |
|
|
|
Зона прододимооти |
|
У///777777/7/, /а Валентная - му зона 7 //"// / уА |
|
Зоно проВодимости |
|
Аит>2эд |
Рис. 2.3. Схема энергетических зон для электронов в проводниках (а, б), полупроводниках (в) и изоляторах (г)
заполнена и зона проводимости свободна от электронов. Однако у полупроводников расстояние между заполненной зоной и зоной проводимости мало, т. е. Aw < 2 эВ (рис. 2.3, а), а у диэлектриков — велико, т. е. Aw > 2 эВ (рис. 2.3, г). Связь концентрации свободных электронов пе с шириной запрещенной зоны для кристаллов при 300 К представлена ниже:
Дш, эВ.................... 10 3 2 1 0,5 0,1
п„ м~3................................. 1(Г5Э 10 10® 1017 102' 1024
Следует отметить, что свободные электроны есть во всех твердых телах, как в проводниках, так и в изоляторах; разница состоит в их количестве.
При наложении электрического поля возникают силы, заставляющие электроны дрейфовать — двигаться вдоль поля; на хаотическое тепловое движение накладывается упорядоченное движение со скоростью дрейфа. Пользуясь законами классической физики, можно оценить ее порядок по сравнению с тепловой скоростью.
Полагаем, что движение электрона, как частицы с массой те и зарядом е, под действием поля Е и ускоряющей силы еЕ происходит в течение времени т = Я/v, где v — средняя квадратичная скорость электрона (тепловая, так как скоростью дрейфа пренебрегаем из-за сравнительной малости), а Я—средняя длина свободного пробега электрона (пробег). Движение с ускорением еЕ/m за время т разгонит электрон до скорости дрейфа:
TOC o "1-5" h z ve — (eE/me){h/v) = (еЕ/тє)г. (2.1)
Плотность тока
j = neve. (2.2)
Подставляя значение ve, получим
j = {ne2/m,){K/v)E. (2.3)
Получаем закон Ома в форме
/ = уЕ,
где у — электрическая проводимость:
V = (пе2/те) т. (2.4)
Величину
b = Ve/E - (е/те)(Я/v) — ех/те (2.5)
называют подвижностью носителя тока (электрона), а уравнение (2.5) известно как уравнение Ланжевена. Тогда
у = j/E = neve/E = neb. (2.6)
Эти формулы применяют для простейшей модели электрона. Реальный пробег электрона в твердом теле, зависящий от его (электрона) подвижности, значительно больше межатомных рас
стояний и составляет десятки (а при низких температурах даже сотни) нанометров, что объяснимо только с учетом волновых свойств электрона.
ПРОВОДНИКИ
Из формул (2.3) и (2.6) видно, что электрическая проводимость прямо пропорциональна числу свободных электронов п, пробегу К и обратно пропорциональна скорости v, которые могут меняться от вещества к веществу. Пробег электрона ограничен тепловыми колебаниями атомов и наличием у кристалла различного рода дефектов.
Рост температуры металла ведет к увеличению тепловой скорости электрона, а увеличение амплитуды колебаний ионов в узлах решетки уменьшает пробег К электрона, поэтому у металлов с увеличением температуры и пластической деформации проводимость уменьшается.
Число заряженных частиц в металле не зависит от силы тока, поэтому проводимость (и сопротивление) металла при данной температуре постоянна. Закон Ома и падение потенциала имеют линейную форму.
ПОЛУПРОВОДНИКИ
В полупроводниках при повышении температуры электроны могут переходить из нижней зоны (валентной) через зазор в верхнюю зону (проводимости). Таким образом, полупроводники, в отличие от металлов, при высоких температурах резко увеличивают проводимость, а при низких — приближаются к изоляторам. Перенос зарядов может быть электронным и дырочным.
Введение примесей в полупроводники может уменьшить зазор до 0,05 эВ. Это происходит, например, при добавках в кристаллы
|
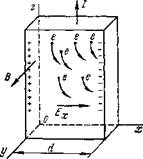
Рис. 2.4. Отклонение носителей тока в твердом теле магнитным полем (эффект Холл а) |
четырехвалентных кремния или германия, пятивалентных мышьяка или сурьмы, которые являются «донорами» свободных электронов, обеспечивающих электронную негативную /г-проводимость. Наоборот, с добавкой «акцепторов» — трехвалентных индия или галлия — полупроводник приобретает дырочную, позитивную р-проводи - мость.
Знак носителей тока и их относительное число в твердом теле можно обнаружить с помощью эффекта Холла. Если вдоль пластинки, помещенной поперек магнитных силовых линий В (рис. 2.4), идет ток /, то на заряженную частицу е, движущуюся со ско
ростью v, будет действовать сила Лоренца F в направлении, перпендикулярном полю и току. Иными словами, в этом направлении возникает электрическое поле напряженностью Ex=vB, а между гранями пластины — разность потенциалов V=vBd. Ее направление и значение определяются знаком и числом носителей заряда.
ЭЛЕКТРОЛИТЫ
Жидкости-электролиты представляют собой растворы каких - либо веществ в воде, либо расплавы солей сульфидов, окислов и т. п. Ионы, находившиеся ранее в узлах кристаллической решетки, в электролите приобретают большую подвижность и могут служить носителями тока. Проводимость электролита зависит от природы, концентрации и коэффициента активности ионов. Все эти параметры сильно зависят от температуры электролита. В растворе ионы обычно менее активны из-за сольватирования их молекулами растворителя, что видно из приведенных ниже данных В. В. Фролова о числе ионов п, и удельной проводимости у в насыщенном растворе (числитель) и в расплаве NaCl (знаменатель) :
л„ 1 м1 ............................... 0,6- 1028/3- 1028
Y....................................... 20/360
Проводимость электролитов подчиняется закону Ома в широких пределах благодаря перераспределению скоростей и энергии ионов. Однако в связи с тем что у поверхности электродов, находящихся в электролите, происходит разрядка ионов, в этих зонах нарушается линейность в падении потенциала и создается повышенное напряжение — анодное и катодное.
ГАЗЫ
Молекулы газа нейтральны, поэтому газ обычно — хороший изолятор и может проводить электрический ток лишь при условии, что в него вводятся извне или генерируются внутри заряженные частицы. Приложив, например, достаточно сильное электрическое поле, можно вызвать нарушение изолирующих свойств газа (пробой) и ионизацию его, вследствие чего он сможет пропускать значительные токи.
У большинства газов в проводящем состоянии носителями зарядов служат электроны и положительные ионы, хотя в некоторых случаях эту роль выполняют и отрицательные ионы.
Предположим, что в 1 м3 газа имеется пе и щ электронов и ионов (однозарядных, положительных), несущих заряды —ей +е соответственно. Под действием напряженностью Е возникают силы еЕ и частицы движутся вдоль поля со средними скоростями дрейфа ve и а,. Перенос зарядов в направлении Е соответствует плотности тока
/' = neeve + ntev,.
В связи с тем что масса иона т, на 3...4 порядка больше, подвижность иона обычно соответственно меньше, поэтому приближенно принимают
j « neeve. (2.7)