Подвижный точечный источник на поверхности полубесконечного тела
По поверхности массивного тела прямолинейно и равномерно со скоростью v перемещается непрерывно действующий точечный источник теплоты постоянной мощности д. Выберем неподвиж
ную декартову систему координат, начало которой совместим с точкой Оо положения точечного источника теплоты в момент времени t - 0 начала его действия. Оси 0о*О и ОоД) выберем в граничной плоскости тела, причем ось Oqxq совместим с направлением перемещения источника, ось 0ozO направим в глубь тела (именно такое направление координатных осей принято в классической теории распространения теплоты при сварке).
При постоянной скорости движения источник в момент времени t будет находиться в некоторой точке О на расстоянии vt от начала координат 0Q - Выберем подвижную декартову систему коор-
|
|
|
Vt У |
X |
А(х, 0,0) |
|
|
----- “І |
I---------- |
) _ _ |
|
|
Оо |
О > |
•0 |
ДЧ), Л |
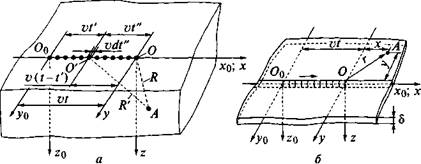
Рис. 6.10. Схемы к расчету температурных полей от подвижных источников:
а - подвижный точечный источник на поверхности полубесконечного тела; б - подвижный линейный источник в бесконечной пластине; в - подвижный плоский источник в бесконечном стержне
динат, начало которой совместим с точкой О текущего положения источника. Оси Ох, Оу и Oz подвижной системы координат направим аналогично осям неподвижной системы координат Оо^о^о^о (рис. 6.10, а).
Пусть в некоторый момент времени /' после начала нагрева источник находится в точке О' с координатами (vt 0, 0). За беско
нечно малый промежуток времени df источник выделяет элементарное количество теплоты dQ = qdt Выделенное в момент времени Ґ в точке О' элементарное количество теплоты dQ, распространяясь в течение времени t - t вызовет к моменту времени t в
точке А массивного тела с фиксированными координатами (xq, уо,
го) изменение температуры
|
(лгр - Vt') + Уо + Zp 4a(t-t') |
|
^ (О=—і 2qdt єхр cpsj[4na(t-t')f |
2 , 2 , 2 ^
где (jco - vt')2 + уо +zq - квадрат расстояния от точки О' до точки А. Множителем 2 в числителе выражения (6.16) учитываем наличие адиабатической границы (плоскости хо^ОЛ))-
Согласно принципу наложения суммарное изменение температуры в точке А массивного тела от действия подвижного источника в течение времени t может быть вычислено интегрированием по формуле
ТА«) = Ты + )аТА{1'). (6.17)
О
В неподвижной системе координат температурное поле точечного подвижного непрерывно действующего источника постоянной мощности, перемещающегося по поверхности полубесконеч - ного тела с постоянной скоростью, с учетом (6.16) и (6.17) выражается формулой
T(xo, yQ, Zo, t) =
|
^ (*0 - Vt')2 + >’о + Zp |
|
dt (6.18) |
|
4a(t-t') |
|
= тн + J г-2- - ехр О cp^[4na(t - г')] |
Выражение для температурного поля (6.18) упрощается, если рассматривать процесс в подвижной системе координат Oxyz, связанной с подвижным источником теплоты. Запишем координаты неподвижной точки А массивного тела в подвижной системе координат:
x = x0-vt; у = Уо z = z0.
Введем переменную времени т = t - Ґ, выражающую длительность процесса распространения тепла элементарного источника.
|
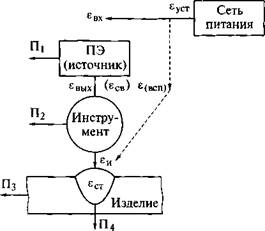
Рис. 1.6. Обобщенная схема баланса энергии сварочного процесса |
|
|
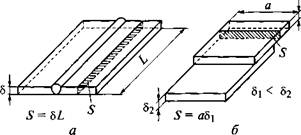
|
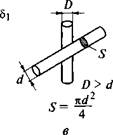
Рис. 1.7. Схема выбора рабочей площади S для расчета удельной энергии сварки стыковых (а), нахлесточных (б) и крестообразных (в) соединений |
|
|
Обозначения удельной энергии на различных стадиях преобразования в схеме баланса энергии (см. рис. 1.6) приняты следующие:
8ВХ - энергия, получаемая сварочной установкой от сети питания; она может использоваться непосредственно на сварку (єсв) и вспомогательные операции (євсп);
Пі - потери энергии в сварочном источнике, с их учетом энергия єсв составит: єсв = гвх-Пі;
П2 - потери в инструменте при передаче энергии изделию; еи - энергия, введенная в изделие: ги = гсв - П2;
Пз - потери энергии в изделии на теплопроводность;
П4 - потери уноса (с испарившимся или выплавленным материалом);
8СТ - энергия, аккумулированная в зоне стыка: sCT = ~ (Пз +
+ П4).
Потери уноса характерны главным образом для резки, но могут возникать и при высокоинтенсивных процессах лучевой сварки.
Отдельные ступени передачи энергии в схеме ее баланса в зависимости от вида сварочного процесса могут существенно изменяться и даже отсутствовать совсем. Например, носитель энергии (инструмент) в термических процессах - это луч, дуга или пламя, а при контактной сварке - сам нагретый металл в зоне контакта.