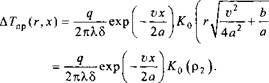Подвижный нормально-круговой источник
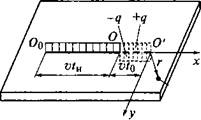
Процесс нагрева пластины движущимся равномерно и прямолинейно нормально-круговым источником постоянной мощности q рассмотрим с использованием принципа наложения аналогично тому, как это было сделано в разд. 6.6.2 для подвижного линейного источника теплоты. Допустим, что источник теплоты вышел из точки Оо и за время t продвинулся в точку О (рис. 6.21). Чтобы учесть распределенность потока теплоты, создаваемого заданным источником, воспользуемся приемом, рассмотренным в разд. 6.11.1, т. е. заменой нормально-кругового источника теплоты линейным источником, теплота которого в точке О выделилась раньше - в
момент времени t - tQ. Формально это можно представить так, что вместо реального нормально-кругового источника теплоты
движется некоторый фиктивный линейный источник с опережением по времени на (q и
|
Л(х, у) |
|
|
по расстоянию на Этот фиктивный источник теплоты находится в точке О'. Очевидно, что на участке ОО реально никакой теплоты не выделя - Рис. 6.21. Эквивалентная схема для
лось (фиктивная часть процес - расчета температур от подвижного
са); поэтому для учета этого нормально-кругового источника в
/ пластине
обстоятельства в расчетную
схему необходимо ввести сосредоточенный фиктивный сток теплоты той же мощности, который действовал только на отрезке ОО (см. рис. 6.21).
Расположив для удобства подвижную систему координат в точке 0 по аналогии с выражением (6.21) и с учетом (6.50) запишем выражение для приращения температуры в произвольной точке А :
|
А Т,=- |
|
(6.52) |
|
*0 - fexp о |
|
dx х |
|
4а |
|
/ л |
t+to |
/ |
[_.2 1 |
2 ^ |
|
f VX. ) |
f exp |
_ |
v — + b |
r x-------- |
|
J r 0 |
V |
4 a |
4ax У |
|
Ш8 |
|
ехр |
|
dx X |
|
- + Ь |
|
х — |
|
4ах |
Выражение (6.52) может быть записано более компактно с использованием коэффициента теплонасыщения (см. разд. 6.8):
АТ = АТпр ехр(Ц))[>2 (Р2> т + Ч)~ т2 (Р2< Ч)]> (6-53)
где
|
/ 2 V 4 а |
|
ґ 2 ' v и + 6 v 4а ч у |
|
(6.54) |
|
то |
|
Р2=Г |
|
4а2 |
|
В предельном состоянии при t ко упрощается: |
оо выражение (6.53) несколь-
АГ = АТпР ехр(^о)[1 ~ V2 (р2’то)]' (6-55>
Значение ДГпр вычисляют по формуле (6.26). При выполнении расчетов следует помнить, что начало подвижной системы координат не совпадает с центром нормально-распределенного источника, а находится впереди него на расстоянии vto, т. е. в месте нахождения фиктивного линейного источника (точка О на рис. 6.21). С увеличением коэффициента сосредоточенности источника к постоянная времени to стремится к нулю, и температурное поле подвижного нормально-кругового источника приближается к температурному полю подвижного линейного источника.
Формулы, описывающие другие случаи нагрева тел распределенными источниками теплоты, можно найти в специальной литературе.
Пример 6.1. Лист из низкоуглеродистой стали толщиной 5 = 2,5 мм нагревают пламенем газовой горелки, перемещающейся со скоростью 9,6 м/ч = 0,26 см/с. Эффективная мощность пламени q = 2,3 кВт; диаметр пятна нагрева d = 6,2 см. Необходимо оценить температуру листа под центром пламени. Теплоемкость стали ср = 5 Дж/(см3 • К); коэффициент теплопроводности X = 0,4 Вт/(см-К); коэффициент температуроотдачи листа b = 0,0064 с~1.
Решение. Считая пламя горелки нормально-круговым источником теплоты, определяем коэффициент его сосредоточенности по формуле (5.28):
|
|
Находим коэффициент температуропроводности стали:
а = — = = 0,08 см2/с.
ср 5
Используя формулу (6.46), вычисляем постоянную времени распределенного источника:
|
1 |
1
= 10 с.
4 ак 4-0,080,31
Определяем расстояние от начала подвижной системы координат до центра пламени:
г = vt0 = 0,26 ■ 10 = 2,6 см.
Вычисляем безразмерные критерии расстояния (р2) и времени (то)*
|
|
|
_^ + М^ = 4,29; 4-0,08 0,08 |
|
Для расчета приращения температуры используем формулы предельного состояния (6.55) и (6.26): |
|
|
|
Определяем по номограмме (см. рис. 6.15, 6) значение коэффициента теплонасыщения: |/2(4,29; 2,17) = 0,51, по таблице определяем А^0(4,29) = = 0,00808 и вычисляем приращение температуры: |
|
= лгпр єхр (Ч )[i - v2 (рг. то)]; |
|
/ |
д Т =--------- ?300 ехр (4,22 + 0,064) • 0,00808 • (1 - 0,51) = 1050 К.
6,28-0,4-0,25 V і >
Таким образом, лист под центром пламени нагревается на 1050 К.