ОСНОВНЫЕ ПОНЯТИЯ И ЗАКОНЫ В РАСЧЕТАХ ТЕПЛОВЫХ ПРОЦЕССОВ ПРИ СВАРКЕ
СХЕМЫ НАГРЕВАЕМОГО ТЕЛА
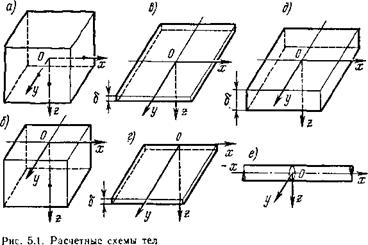
Формы тел, нагреваемых при сварке, весьма разнообразны. Распространение теплоты существенно зависит от формы и размеров тела. Точный учет конфигурации тела может привести к таким усложнениям расчета, что его практическое использование окажется затруднительным. Поэтому во всех тех случаях, когда пренебрежение второстепенными особенностями формы тела не приводит к большим погрешностям расчета, целесообразно упрощать формы рассматриваемых тел, сводя их к простейшим. Разумеется, грамотное применение такой схематизации должно основываться на четком понимании физической сущности процесса в целом. Обычно выбирают одну из следующих основных схем.
Если границы тела не влияют на распространение теплоты, его можно заменить бесконечным телом, у которого имеется неограниченная протяженность по всем трем направлениям х, у, z (рис. 5.1, а).
Полу бесконечное тело представляет собой массивное тело с одной ограничивающей плоскостью 2 = 0 (рис. 5.1, б). Остальные поверхности находятся на значительном удалении и не влияют на распространение теплоты.
Бесконечная пластина представляет собой тело, ограниченное двумя параллельными плоскостями 2 = 0 и 2 = 6. Прн ис-
|
|
пользовании этой схемы всегда предполагают, что температура по толщине листа равномерна, а теплота может распространяться только в плоскости с координатными осями х и у (рис. 5.1, в).
Полубесконечная пластина представляет собой тело, ограниченное двумя параллельными плоскостями 2 = 0, 2 = 6 и плоскостью у = 0 (рис. 5.1, г). Остальные условия те же, что и у бесконечной пластины.
Плоский слой представляет собой пластину, у которой температура точек тела по толщине неравномерна. Эту схему применяют в тех случаях, когда толщина тела не настолько велика, чтобы можно было пренебречь влиянием ограничивающей плоскости 2 = б и считать тело полубесконечным (рис. 5.1, д).
Бесконечный и полубесконечный стержни представляют собой тела с прямолинейной или криволинейной осью; температура в пределах поперечного сечения стержня равномерна (рис. 5.1, е).
Помимо названных схем в практике расчетов используют также и другие простейшие схемы, например сплошной цилиндр, тонкостенный цилиндр. В приведенных схемах тел могут использоваться как декартовы, так и цилиндрические или полярные координаты.
ТЕПЛОФИЗИЧЕСКИЕ ВЕЛИЧИНЫ И ПОНЯТИЯ
Температура характеризует степень нагретости тела и представляет собой одну из важнейших тепловых величин. В шкале Кельвина нижней границей температурного промежутка служит точка абсолютного нуля. Абсолютная температура выражается в кельвинах (К, 1 К= 1°С). Температура таяния льда соответствует 273,16 К. В настоящем разделе для обозначения абсолютной температуры использован символ Т, для приращения или разности температур — символ АТ, для начальной температуры тела — ТИ, для температуры окружающей среды — Тс.
Температурное поле есть распределение температур в теле в конкретный момент времени; оно может выражаться как в абсолютной температуре (Т), так и в приращении температур (АТ) по отношению к начальной температуре тела ТИ. В общем случае температурное поле может быть функцией не только координат X, у, 2 отдельных точек, но и времени t:
Т = Т (х, у, 2, t). (5.1)
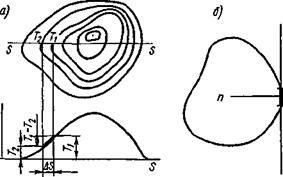
Формула (5.1) описывает объемное температурное поле. Оно может быть также плоским Т = Т (х, у, t) или линейным Т = = Т (х, t). Для наглядности температурные поля часто представляют графически в виде изотерм (рис. 5.2, а). Изотермической поверхностью или изотермической линией называется геометрическое место точек тела, имеющих одинаковую температуру. От точки к точке температура тела может изменяться. Изменение температуры в направлении SS на длине бесконечно малого отрезка dS называется градиентом температуры в рассматриваемой
|
|
|
ydF |
|
t |
|
t |
|
Рис. 5.2. Изображение температурного поля изотермами: а — изменение температуры по направлению SS; б — касательная И и нормаль пп к изотерме |
|
•n |
|
т |
|
s |
точке по данному направлению SS
|
(5.2) |
grad Tss = dT/dS.
Градиент температуры в точке максимален по направлению нормали пп к изотерме (рис. 5.2,6).
Скорость изменения температуры в данной точке поля с координатами х0, уо, 2о в данный момент времени to выражается частной Производной от температуры по времени:
|
(5.3) |
Щ (х0, Уо, zo, 6>) = dT/dt.
Количество теплоты Q измеряется в джоулях (Дж). Одна международная калория равна 4,1868 Дж.
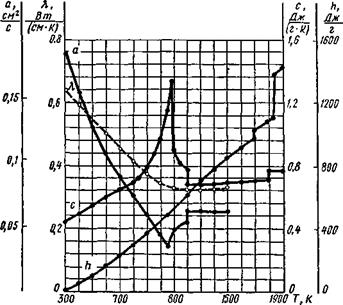
Удельное количество теплоты (теплосодержание) h выражает количество теплоты, сообщенное телу массой 1 г, при нагреве его от температуры Т до температуры TV При технических расчетах теплосодержание тела отсчитывают обычно от нормальной температуры (293 К), а не от абсолютного нуля. Вне критических точек теплосодержание в металлах с ростом температуры возрастает монотонно. В критических точках, соответствующих аллотропическим и фазовым превращениям, происходящим с поглощением или выделением теплоты, оно изменяется скачкообразно (рис. 5.3).
Удельная теплота фазового превращения I определяется, как количество теплоты, поглощаемой или выделяемой единицей массы материала при изотермическом процессе фазового превращения.
Истинная удельная массовая теплоемкость с есть количество теплоты, необходимое для изменения на одии кельвин температуры единицы массы тела (см. рис. 5.3). В расчетах бывает удобно пользоваться средней удельной массовой теплоемкостью в данном интервале температур от Ті до Т^:
|
Рис. 5.3. Теплофизические свойства низкоуглеродистой стали с 0,1% С: теплосодержание Л, отсчитываемое от 300 К, истинная теплоемкость с, теплопроводность Я, температуропроводность а |
Ст = (А2 - hi)/(T2 - Ті). (5.4)
В расчетах может использоваться истинная С и средняя С„, удельная объемная теплоемкость, которая связана с массовой удельной теплоемкостью следующими соотношениями:
С == Ср, С т === Сглр, (^*^)
где р — плотность тела в нормальных физических условиях.
Закон теплопроводности (закон Фурье). В общем случае передача тепловой энергии может осуществляться тремя способами: теплопроводностью, конвекцией, лучистой энергией (радиацией).
Для передачи теплоты в твердых телах характерен первый способ.
В жидкостях теплота передается конвекцией и теплопроводностью; в газах — в основном конвекцией и радиацией; в вакууме — только радиацией. Закон теплопроводности устанавливает количественную связь между теплопроводностью металла, градиентом температуры и тепловым потоком в твердом теле.
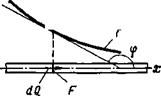
Рассмотрим передачу теплоты в стержне, температура по длине которого переменна (рис. 5.4). Очевидно, теплота будет перетекать от более нагретых к менее нагретым участкам. Количество теплоты dQx, протекающее вследствие теплопроводности за вре
мя dt через попере ное сечение F, пропорционально градиенту температуры dT/dx в рассматриваемом сечении, площади сечения F и времени dt:
|
Рис. 5.4. Распределение температуры в стержне |
|
|
dQx = k{—dT/dx)Fdt. (5.6)
Знак минус в формуле (5.6) означает, что поток теплоты направлен в сторону, противоположную возрастанию температуры. Коэффициент пропорциональности к называется коэффициентом теплопроводности.
В общем случае температурного поля закон Фурье записывается следующим образом:
dQn = k{—dTJdn)dFdt. (5.7)
Тепловой поток — это количество теплоты, проходящее через рассматриваемое сечение (поверхность) в единицу времени:
|
(5.8) |
Ф = dQ/dt.
В случае, представленном на рис. 5.4, тепловой поток означает количество теплоты, проходящее через поперечное сечение стержня за 1 с.
|
|
|
(5.9) |
|
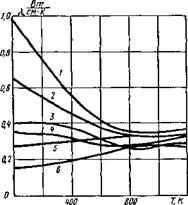
Рис. 5.5. Теплопроводность X различных марок стали в зависимости от температуры: / — электролитическое железо; 2 — иизко- углеродмстая сталь с 0,1% С; 3 — углеродистая сталь с 0,45% С, 0.08% Si. 0,07% Мп; 4 — низколегированная сталь с 0,10% С, 0,02% Si, 0,4% Мп, 4,98% Сг: 5 — сталь с 1,52% С, 0,38% Si, 0,38% Мп, 13,1% Сг; 6 — хромоннкслевая коррозионно-стойкая сталь типа 18—8 |
Удельный тепловой поток определяется тепловым потоком, приходящимся на единицу площади (индекс «два»):
|
Теплопроводность к характеризует способность тел проводить теплоту. Численно коэффициент к выражает количество теплоты, протекающее через единицу изотермической поверхности в единицу времени, если изменение температуры по направлению нормали составляет 1 К на 1 см. Теплопроводность металла существенно изменяется в зависимости от температуры и химического состава материала. На рис. 5.5 показано изменение к в зависимости от температуры. |
<72 = d<$)/dS.