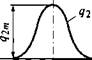
Мгновенный нормально-круговой источник
|
Определим приращение температуры в тонкой пластине в момент введения теплоты мгновенным нормально-круговым источником, который действовал в течение бесконечно малого промежутка времени dt (рис. 6.20). Количе- |
|
ство теплоты, введенной на участок поверхности площадью dxdy, составит dQ - q2dxdydt. Так как пластина тонкая, теплота мгновенно распространится равномерно по толщине 6 и температура элементарного объема bdxdy повысится на |
|
dT = - dQ =32&.' (6.43) |
|
cpbdxdy срЪ |
|
Подставив в (6.43) значение qi из вы- |
|
Рис. 6.20. Схема нагрева ражения (5.27), получим искомое вы - тонкой пластины нормаль - ражение: но-круговым источником |
|
теплоты |
|
срб |
|
где к - коэффициент сосредоточенности источника. Из выражения (6.44) следует, что мгновенный нормальнокруговой источник теплоты вызывает в пластине приращения температур так же, как и тепловой поток, распределенные по нормальному закону. Сравнивая выражение (6.44) с выражением (6.2) для схемы мгновенного линейного источника в пластине, нетрудно заметить, что они построены однотипно и могут описывать одинаковые распределения температур по радиусу г. На основании этого подберем фиктивный мгновенный линейный источник, теплота которого Q, распространяясь по пластине в течение некоторого промежутка времени приводит к такому же распределению температур, какое вызвано рассматриваемым нормально-круговым источником: |
|
(6.45) |
|
|
|
6 |
|
£ |
|
г |
|
|
|
г |
|
|
Прежде всего приравняем показатели экспоненциальных функций в выражениях (6.44) и (6.45). Из полученного соотношения легко выразить длительность распространения теплоты фиктивного линейного источника:
Таким образом, теплота от мгновенного линейного источника, распространяясь в течение промежутка времени to, приводит к распределению температуры с таким же коэффициентом сосредоточенности источника к, как и у заданного нормально-кругового
источника. Фиктивное время to, зависящее от коэффициента сосредоточенности распределенного источника и температуропроводности материала, называют постоянной времени при нагреве данного материала заданным нормально-круговым источником.
Приравняем теперь выражения, стоящие перед экспоненциальными функциями в формулах (6.44) и (6.45) для определения энергии фиктивного источника:
|
(6.47) |
Q _ 4lmdt ср5(4яа/0) ср5
|
(6.48) |
Используя выражения (5.29) для qjm и (6.46) для to, получаем, что энергия мгновенного линейного источника равна энергии мгновенного нормально-кругового источника:
Q = qdt.
Таким образом, распределение температуры, вызванное в тонкой пластине мгновенным действием нормально-кругового источника, можно рассматривать как результат фиктивного процесса
(продолжительностью to) распространения теплоты мгновенного линейного источника, обладающего такой же энергией. Очевидно, что процесс выравнивания температуры при таком распределении эквивалентен последующей стадии процесса распространения теплоты от мгновенного линейного источника, т. е
|
|
В связи с изложенным целесообразно сравнивать по вводимой энергии все существующие сварочные процессы. Этот критерий поможет выявить общие физические закономерности, связывающие их между собой.