ТЕОРИЯ сварочных процессов

Кинетика гомогенных процессов

КИНЕТИКА ХИМИЧЕСКИХ И ДИФФУЗИОННЫХ ПРОЦЕССОВ

Сварка металлов плавлением представляет собой высокотем­пературный быстропротекающий процесс, сопровождающийся химическими реакциями между металлом и средой (атмосфера дугового промежутка, шлаки, полученные плавлением флюсов или электродных покрытий), а также диффузионными процесса­ми, особенно интенсивно развивающимися при высоких темпера­турах (например, диффузионное соединение металлов в вакууме, предложенное Н. Ф. Казаковым).

Скорости химических реакций и диффузионных процессов характеризуются изменением концентрации вещества во времени, т. е. изменением числа частиц в единице объема в единицу вре­мени.

При химических реакциях атомы нли молекулы веществ, всту­пающих в реакцию, должны войти в тесное соприкосновение — столкновение, перестроить свои атомные или молекулярные орбитали, с тем чтобы они могли образовать новые химиче­ские связи н построить новые молекулы продуктов реакции. В ре­зультате этого взаимодействия концентрация начальных продук­тов будет уменьшаться, а конечных — увеличиваться. Химичес­кие реакции могут быть необратимыми, т. е. идущими только в одном направлении, но могут быть и обратимыми, направление которых будет зависеть от внешних условий — р, Т, С. Обрати­мые реакции не доходят до конца, а только до состояния равно­весия (см. п. 8.3, 8.4).

Условия для столкновения реагирующих частиц между собой будут меняться в зависимости от фазового строения реагирую­щей системы, т. е. от ее гомо - или гетерогенности.

По типу развития химических реакций их можно разделить согласно предлагаемой схеме:

Число частиц в единице объема определяет при данной темпе­ратуре число столкновений и, следовательно, будет связано со скоростью химической реакции уравнением

д=КЬС/Ы, (8.94)

где v — средняя скорость реакции; К — константа скорости; С — концентрация реагирующих молекул; t — время.

Так как концентрация молекул, вступающих в реакцию, уменьшается, а скорость реакции тоже переменна, то истинная скорость реакции будет представлять собой первую производную от концентрации по времени:

v = KdC/dt. (8.95)

При диффузионных процессах также происходит изменение концентрации одного вещества — диффузанта вследствие про­никновения его в среду, заполненную другим веществом. Движу­щей силой изотермической диффузии будет градиент концентра­ций, и диффузия всегда направлена от большей концентрации к меньшей.

Задача о диффузии в газовой среде решается методами кине­тической теории газов, так как в этом случае не требуется особой энергии активации для проникновения одного газа в другой. Ес­ли диффузия происходит в конденсированных фазах (жидкая, твердая), то в этом случае для перемещения частиц диффузанта требуется энергия активации, так как в жидкости и в кристалле частицы между собой связаны значительной энергией межатом­ного или межмолекулярного взаимодействия, находясь на малых расстояниях друг от друга. Скорость диффузии в этом случае будет значительно меньше.

При переходе диффундирующих атомов границы раздела двух фаз (например, из жидкой в твердую нли наоборот) необходимо учитывать коэффициент распределения, так как равновесные кон­центрации в данном случае не будут равны между собой. Такой процесс называют гетеродиффузией.

ЭНЕРГИЯ АКТИВАЦИИ И ЗАВИСИМОСТЬ

ПРОЦЕССОВ ОТ ТЕМПЕРАТУРЫ

Энергией активации называется энергия, необходимая для приведения одного моля реагирующих веществ в реакционно­способное состояние.

Эта энергетическая функция обобщает все вопросы строения и состава реагирующих веществ и способов их возбуждения (термическое, радиационное, электронный удар). Таким образом, далеко не все столкновения молекул реагирующих веществ будут активными, а только те, которые будут обладать энергией, рав­ной или большей энергии активации.

Для гомогенных реакций в газовой фазе можно использовать уравнение Максвелла — Больцмана для распределения энергий в объеме газа при данной температуре:

п/п 0=вн—« (8.96)

где п — число молекул, обладающих энергией є, превышаю­щей наиболее вероятное значение энергии ео; «о — число моле­кул, обладающих наиболее вероятным запасом энергии ео; k — постоянная Больцмана; Т — температура.

Из уравнения видно, что чем больше разность значений е — 60, тем меньше будет отношение п/по н тем меньше будет чис­ло активных молекул п. Прн повышении температуры отношение п/по будет расти и число активных молекул будет увеличиваться, т. е. будет расти константа скорости химической реакции К [уравнение (8.94)].

С. Аррениус и Я. Вант-Гофф независимо друг от друга при­шли к уравнению, связывающему константу скорости, температу­ру и энергию активации, причем это уравнение построено по типу уравнения Максвелла — Больцмана:

Кт=Кое~А/т, (8.97)

где Кт — константа скорости химической реакции; Ко — по­стоянный коэффициент; А — энергия активации; R — газовая постоянная; Т — температура.

Если А —оо, т. е. энергия активации очень велика, то Кт—►О, или реакции, требующие высоких значений энергии активации, идут с малой скоростью, так как активные столкновения малове­роятны. Наоборот, если А—>0, то Кт-~Ко, пропорциональному общему числу столкновений, т. е. скорость химической реакции будет очень большой, так как почти каждое столкновение будет активным.

Как правило, энергия активации определяется эксперимен­тально, путем определения констант скорости при нескольких температурах-

1п Кті= ІП Ко — A/(RTi) In Кт2= In Ko-A/(RT2); вычитая эти уравнения друг из друга, получим

1п(Кл//Ст2)=(А/Я) (—і/Гі + 1/Г2)=А(7'1 - Г2)/(/гГ, ГЙ(Я.98)

Влияние температуры на скорость химических реакций. Если Т->■ оо, то Кт->-Ка, т. е. константа Кт сильно растет (экспоненци­ально) и при температурах процессов сварки металлов плавле­нием (103...104 К) скорости взаимодействия будут очень велики и будут приближать состояние к равновесному, которое рассчи­тывается методами химической термодинамики.

Катализ и катализаторы. Катализом называется процесс из­менения энергии активации с целью изменения скорости химиче­ских реакций при той же температуре путем введения в реакци­онную среду катализаторов.

Катализаторами называются вещества, которые ускоряют хи­мическую реакцию (положительные) или снижают ее скорость (отрицательные), но сами й результате химической реакции оста­ются неизменными.

Если катализатор находится в той же фазе, что и участвую­щие в химической реакции вещества, то катализ называют гомо­генным, а если катализатор находится в другой фазе и свое ката­литическое действие оказывает своим поверхностным слоем (твердое тело), то гетерогенным.

Гомогенный катализ по существу сводится к замене одной реакции, идущей с большой энергией активации, двумя или тре­мя (с участием катализатора, в результате выделяющегося в прежнем состоянии), но требующих меньшей энергии активации:

1. А + В — АВ А,.

2. А + К^АК А2<А,

3. АК. + В—AB-fK Аз<Аь

где К — катализатор.

Энергии активации реакций 2 и 3 меньше, чем реакции 1, поэ­тому скорость превращения веществ А и В в АВ будет значитель­но выше. Каталитирующее действие в данном случае будет за­висеть от концентрации катализатора, так как он по существу служит реагентом.

Гетерогенный катализ происходит на границах раздела твер­дое тело — газ или твердое тело — жидкая фаза (раствор). Ме­ханизм каталитического воздействия поверхности твердого тела заключается в адсорбции на поверхности катализатора ре­агирующих между собой молекул, в результате чего их концен­трация в поверхностном слое возрастает на несколько порядков, а под действием энергии адсорбции ослабляются связи между частицами, составляющими молекулы, и, следовательно, снижает­ся энергия активации. Не исключено и химическое взаимодей­ствие между молекулами реагирующих веществ и адсорбента, т. е. катализатора (топохимнческие соединения). Высокоактив­ные катализаторы этого типа — тонко раздробленные металлы, нанесенные на какую-либо подложку, например, платинирован­ный асбест, серебро или палладий, нанесенные на цеолиты, тонко раздробленный никель и т. д.

Каталитическая активность находится в прямой связи с пло­щадью поверхности катализатора.

Некоторые данные о снижении энергии активации химических реакций в присутствии катализатора приведены в табл. 8.8.

Энергии активации диффузионных процессов, как видно, ниже энергии активации химических реакций ввиду того, что молекулы или атомы при диффузии не изменяют своего строения. В данном случае энергия активации будет определяться диффузионной средой и ее строением. Особенно высоки значения энергии акти­вации прн диффузии в твердых металлах и других кристалличе­ских веществах. В твердом теле диффузия может происходить

по объему кристаллического зерна путем замены одного атома в кристаллической решетке другим, но этот путь требует очень высоких энергий активаций, соизмеримых с энергией кристалли­ческой решетки. Например, торий диффундирует в вольфраме объемно, требуя энергии активации 502 кДж/моль. Если диффу­зия идет по границам зерен, где имеется много нарушений крис­таллической структуры — вакансий и дислокаций, то энергия активации составляет 393,5 кДж/моль. При поверхностной диф­фузии тория по вольфраму энергия активации составляет всего 278 кДж/моль (торирование вольфрама). Соответственно резко изменяются коэффициенты диффузии, так как уравнение для коэффициента диффузии аналогично уравнению константы ско­рости химической реакции в зависимости от температуры:

Dr=D0e-WRT (8.99)

где DT—коэффициент диффузии при данной температуре 7; Do — постоянный коэффициент; Q — энергия активации диф­фузии.

Диффузия — необратимый процесс, связанный с большим ростом энтропии, и ее возникновение и развитие, особенно в области высоких температур при сварке, неизбежно.

УРАВНЕНИЯ СКОРОСТЕЙ ХИМИЧЕСКИХ РЕАКЦИЙ

В зависимости от количества реагирующих между собой ве­ществ дифференциальные уравнения скоростей химических реак­ций будут различаться между собой.

Реакции первого порядка (мономолекулярные)

АВ->-А+ В;

•а х х vi=dx/dt=Ki(a — x), (8.100)

где Ki — константа скорости мономолекулярной реакции, представляющая собой функцию температуры и природы реаги­рующих веществ; t — время; а — начальная концентрация ве­щества АВ.

Реакции второго порядка (бимолекулярные)

А + В-^АВ;

а Ь х

V2=dx/dt—Ki(a — x)(b—x), (8.101)

где Кг — константа скорости бимолекулярной реакции, за­висящая кроме температуры и природы реагирующих веществ от способа выражения концентраций; а н b — начальные концен­трации веществ А и В.

Таким образом, порядок реакции соответствует показателю степени, в который входит значение концентрации в уравнение скорости химических реакций.

Реакции высоких порядков (3 и более) встречаются редко, так как в этом случае вероятность одновременного избиратель­ного столкновения трех н более молекул становится малой вели­чиной. Фактически сложные реакции идут через промежуточные стадии, а общую скорость процесса определяет наиболее медлен­но развивающаяся стадия, так как пока она не завершится, остальные стаднн развиваться не могут. Этн элементарные акты химического взаимодействия обычно идут по первому или второ­му порядку. Решение уравнений любого порядка всегда возмож­но, так как при t—0, х=0 и постоянные интегрирования легко определить.

Решение кинетического уравнения для реакций первого по­рядка

dx/dt= Кі(а — х); разделяем переменные и интегрируем:

dx/(a — x)=KidT; -n(a-—x)—Kit-{-C;

при *=0 х—0 и постоянная интегрирования С=— 1па.

Подставляем'значение постоянной интегрирования и получаем

In [a/(a-x)] = Kit, (8.102)

где К — константа скорости первого порядка.

Исследуем полученное выражение:

при х—»а /—► оо, т. е. реакции заканчиваются через бесконеч­но большое время, фактически тогда, когда современными ана­литическими методами уже нельзя уловить изменений в составе системы;

при х—а/2

<о,5=(1/Аі)1п2 =0,693/Аь (8.103)

где to,5 — время, необходимое для превращения половины реагирующего вещества, называемое «периодом полураспада» (или половинным временем).

Для реакций первого порядка оно зависит только от темпера­туры и природы реагирующих веществ. Это уравнение точно опи­сывает ход радиоактивного распада;

решаем уравнение (8.102) относительно концентрации распа­дающегося вещества х;

а[{а — х)=ек' х=а{

Это уравнение позволяет получать информацию о концентрации распадающегося вещества по времени:

а) /=0 *=0, т. е. реакция не начиналась;

б) t=оо х=а—реакция дошла до конца;

в) х=0,5 a <o,5=(l//(i)ln2.

Реакции первого порядка особенно характерны для высоких температур — это диссоциация молекул или ионизация атомов: Н2—2Н; Н2—-Н2М-Є; Н-*Н+ + е, и т. д.

Кривые изменения х во времени при различных значениях Кі приведены на рис. 8.17. На графике указаны также значення периодов полураспада (половинных времен).

Решение кинетического уравнения для реакций второго по­рядка

dx/dt=K2(a — x)(b — x).

Решаем это дифференциальное уравнение с помощью произ­вольных коэффициентов и после подстановки постоянной интег­рирования, полученной при условии *=0; *=0, окончательно имеем

Исследуем полученное выражение: константа скорости реакции второго порядка зависит от кон­центрации (Г

К2 =

Ка

прн а= b уравнение пре­вращается в неопределен­ность и для случая равных концентраций реагирующих веществ требуется иное урав­нение:

А + В - а а

Окончательное решение этого уравнения K2t=—

а— х а а выражение константы скорости.

*2=4- —, (8.108)

/ а а—х ' '

причем размерность скорости сохраняется (t~l, с-1);

для условия равных концентраций для реакции п-го порядка уравнения скорости

dx/dt = KJa — xf. (8.109).

Уравнение (8.109) применяется, в частности, при эксперимен­тальном определении порядка той или иной реакции.

Следует указать, что под влиянием катализаторов порядок реакции может измениться. Так, диссоциация аммиака идет в газовой фазе по уравнению второго порядка, а при каталитиче­ском действии твердого ванадия реакция идет по нулевому по­рядку, т. е. без влияния концентрации реагента, она остается как бы постоянной величиной. Решение уравнений для расчета обратимых гомогенных реакций не рассматриваем ввиду их боль­шой сложности и сравнительно узкого применения таких рас­четов.

УРАВНЕНИЕ КОНЦЕНТРАЦИОННОЙ ДИФФУЗИИ

Процессы переноса вещества путем диффузии связаны с на­личием градиента концентраций диффундирующего вещества в среде, заполненной другим веществом. Процессы диффузии опи­сываются уравнениями законов Фика:

dm — — D(dc/dx)Sdt; I

* ЛСЛ* /Л 2Ч <8Л1°)

~=D(dh/dx2), ]

где т — количество продиффундировавшегося вещества; S— площадь сечения диффузионного потока; t — время; dc/dx — градиент концентраций, отрицательный потому, что диффузия идет от большей концентрации к меньшей; D — коэффициент пропорциональности или коэффициент диффузии.

Интеграл второго уравнения системы (8.110), т. е. второго закона Фика, будет равен для бесконечно длинного цилиндра при взаимной диффузии двух газов следующему выражению:

/тт

с'-=т—-I S ‘-^тО-Ч-тйг)! (8ЛИ)

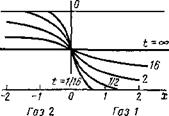
где Со — концентрация в начале процесса диффузии в сечении трубы О—О; <f[x/-j4Dt] — функция, значение которой можно взять из справочника по значениям функций Фурье — Фика.

На рис. 8.18 представлено ре­шение этого уравнения в виде изо - хрон концентраций (линий для постоянного значения времени), причем с увеличением времени при данном значении х (расстояние от начального сечения) концентра­ция возрастает и стремится к зна­чению Со/2. Расчет развития диф­фузионных процессов на основа­нии второго закона Фика сохра­няется для жидких и для твердых сред, но коэффициенты диффузии будут значительно меньше, чем для газообразных систем.

Для газообразных систем коэффициенты диффузии вычисля­ют на основании кинетической теории газов:

й=Ш/ 3, (8.112)

средняя скорость движе-

где К — длина свободного пробега; и ■ ния газовых молекул.

Как видно из уравнения (8.110), размерность коэффициента диффузии сохраняется (м2-с-1).

Некоторые значения коэффициентов диффузии газов приведе­ны в табл. 8.9.

Коэффициенты диффузии в жидкостях на несколько порядков меньше, чем в газах, например коэффициент диффузии магния в жидком алюминии при 973 К составляет 7,54-10~9 м2-с~1, а коэффициент диффузии NaNC>3 в расплавленном KNO3 при 633 К составляет 5,22 • 10~9 м2-с-1.

Коэффициенты диффузии в жидкостях могут быть рассчитаны по уравнению Стокса:

D = -=&-, (8.113)

олцг v ’

где k — постоянная Больцмана; Т — температура; к] — коэффи­циент вязкости среды; г — раднус частицы.

Для твердых кристаллических тел коэффициенты диффузии еще меньше. Например, алюминий, диффундирующий в твердую медь, при температуре 1123 К имеет коэффициент диффузии £ = 2,19ХКГ13 м2-с-1.

Высокая энергия активации диффузии в твердых телах делает коэффициенты диффузии очень малыми согласно уравнению (8.99).

Некоторые данные о константах в этом уравнении приведены в табл. 8.10.

Помимо изотермической диффузии, описываемой уравнениями законов Фика (8.110), перенос атомов может возникнуть под действием различных температур, т. е. в неоднородном темпе­ратурном поле. Такая неизотермическая диффузия может выз­вать перераспределение или сегрегацию компонентов сплава в температурном поле, созданном термическим циклом сварки. Это будет особенно заметно для элементов, обладающих высо­кой подвижностью, например, для водорода Н.