ТЕОРИЯ сварочных процессов

Граница с теплообменом

При сварке на воздухе массивных металлических изделий теп­лоотдача с поверхности, как правило, несоизмеримо мала в срав­нении с отводом теплоты внутрь изделия за счет теплопроводно­сти. Поэтому для массивных тел внешние границы обычно счита­ются адиабатическими.

Для схем пластины и стержня теплоотдача с поверхности мо­жет играть ощутимую роль в формировании температурного поля. В связи с этим теплоотдача с поверхности была учтена в двумер­ном (5.23) и одномерном (5.24) дифференциальных уравнениях теплопроводности. В решениях (6.2) и (6.3) этих дифференциаль­ных уравнений присутствуют экспоненциальные множители е'ы, с помощью которых учитывается свободное охлаждение через по­верхность. Температура пластины или стержня с теплоотдачей всегда ниже температуры изолированной пластины или стержня.

Для каждого момента времени множитель e~bt имеет постоянное значение во всем объеме пластины или стержня.

Одним из простейших случаев использования граничного ус­ловия третьего рода является учет свободного охлаждения тонкой пластины толщиной 5 и объемной теплоемкостью ср, равномерно нагретой до начальной температуры Гн. Закон охлаждения такой пластины описывается дифференциальным уравнением

*L=-b(T-Tc), (6.13)

at

где Ь = 2а/ (ср5) - коэффициент температуроотдачи, 1/с; Тс - тем­пература окружающей среды. Число 2 в выражении для Ъ указыва­ет на то, что теплоотдача осуществляется с двух поверхностей. В случае, когда пластина имеет одну теплоотдающую поверхность, b = а/(ср5).

С учетом начальных условий (Т = Ти при t = 0) решение урав­нения (6.13) можно записать в виде зависимости

= е~01. (6.14)

т*-тс

Для равномерно нагретого стержня дифференциальное уравне­ние процесса свободного охлаждения также имеет вид (6.13), но в выражение для коэффициента температуроотдачи входят периметр р и площадь сечения F стержня:

Ь = ар/ (cpF). (6.15)

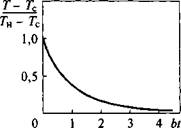
Изменение температуры пла­стины (или стержня) в процессе свободного охлаждения, описы­ваемое экспоненциальной зависи­мостью (6.14), можно проиллюст­рировать графиком, представлен­ным на рис. 6.9. В начале процесса темп охлаждения наиболее высок,

по мере уменьшения разности „ „

, Рис. 6.9. Изменение температуры

температур пластины (или стерж - _ .. v J

' J r v г равномерно нагретой пластины в

ня) и окружающей среды умень - свободного охлаждения

шается и пропорциональная ей скорость охлаждения. С течением

времени температура пластины (или стержня) асимптотически стремится к температуре окружающей среды.