Элементы термодинамики плазмы
ЭЛЕКТРОННАЯ И ИОННАЯ ТЕМПЕРАТУРЫ
Для обычных сварочных дуг, горящих в среде при давлении порядка атмосферного, столб дуги представляет собой плазму. В полностью ионизированной плазме нейтральные частицы отсутствуют.
Плазма дуги квазинейтральна (т. е. почти нейтральна), так как в ней отрицательный заряд электронов почти точно нейтрализует положительный заряд ионов.
|
р малое |
|
та |
Однако так как электроны гораздо подвижнее, чем положительные ионы, то поле заставляет электроны быстро уходить к аноду и столб дуги имеет положительный потенциал относительно катода.
|
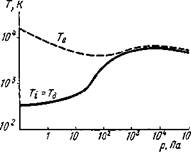
Рис. 2.16. Электронная температура Те и температура газа Гд = Ті в столбе дуги в зависимости от давления |
Термическое равновесие в дуговом промежутке будет полным, когда частота появления всех возмож-
|
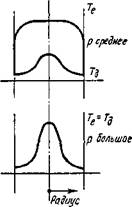
Рис. 2.17 Радиальное распределение температур Те и Гд в столбе дуги |
ных энергетических состояний удовлетворяет распределению Максвелла — Больцмана. В плотной среде столба дуги столкновения между частицами приводят к быстрому установлению локального равновесного состояния. Напротив, в разреженной плазме, где столкновения частиц редки, могут длительное время существовать состояния, далекие от равновесия. Столкновения частиц становятся редкими и при высоких температурах в так называемой горячей плазме, когда энергия теплового движения Й7'= 10... 100 эВ и более. Плазма, имеющая кТ порядка 1 эВ (11 600 К), в физике считается холодной плазмой.
Основное понятие термодинамики — понятие температуры, которая характеризует значение энергии и ее распределение между частицами вещества. В разреженной или в горячей плазме электронная Те и ионная Т; температуры не равны между собой (рис. 2.16), но с увеличением давления газа их значение и распределение по сечению столба дуги становятся почти одинаковыми (рис. 2.17). Ионная температура близка к температуре газа
Ті* г..
Рассмотрим кратко границы применения термодинамических характеристик в сварочной плазме.
ТЕРМИЧЕСКОЕ РАВНОВЕСИЕ
Показателем термического равновесия в системе служит равенство температур всех ее составляющих. Покажем, например, что в дуге существует локальное термическое равновесие, которое устанавливается достаточно быстро.
Электроны при плотности тока і от электрического поля F получают в 1 м3 за 1 с энергию
w = jE = eneVeE - епеЬеЕ2 = е2ПеЕ2т/те, (2.25)
где be=Ve/E — подвижность электрона; о = еЕт/т — см. формулу (2.1); т — время пробега электрона.
Для определения полного числа условных столкновений, испытываемых электроном за 1 с, надо сложить частоты v всех видов столкновений: с иоиами (vei= 1/т<>,•), с атомами (vea= 1/теа) и электронами vec= 1/т«. (2.26)
Однако для плотной плазмы важно наличие тяжелых s-час - тиц (ионов, атомов), при столкновении с которыми вектор скорости электронов претерпевает хаотическое (в среднем равномерное) рассеяние. При этом становится возможным превращение кинетической энергии электронов в энергию беспорядочного теплового движения других частиц. Полная нерегулярность направлений скорости электронов достигается уже после небольшого числа столкновений. Формула для res имеет вид
|
(2.27) |
Т es—'ke/Ve^ 1 /(veneQe)— 1 /{VeSe).
Положим пе= 1024 м_3; ис= 10® м/с (см. § 2.1).
Сечение Рамзауэра для столкновений электронов с тяжелыми частицами Qe= 10“ м2 (см. рис. 2.12), а
Se = neQe= 1024 ■ 1(Г20= 104 м~'.
Тогда для плазмы дуги в аргоне получим время пробега: Tes= 1/(Ю8-10") ж 10~12 с,
т. е. время установления равновесия мало.
При каждом столкновении электрон отдает свою избыточную (но не полную) энергию, полученную от поля Е пропорционально отношению 2 me/ms.
Таким образом, для выравнивания температуры газа и электронов необходимо число ms/(2те)= 3..Л0 соударений (здесь 103 соответствует примерно отношению масс в водородной плазме, где msttlM0me, а 10а относится к аргоновой или ртутной плазме). В то же время электроны непрерывно получают энергию от поля. Поэтому устанавливается электронная температура Те, которая превышает температуру газа Гд на небольшую величину Д7 Энергия jE, полученная электронами от поля, должна быть равна энергии, отдаваемой электронами частицам газа при столкновении вследствие разности температур:
'!Е = е2ПеЕ2те^/те = (3/2)к{Те — 7'J(2me/ms)«cves. (2.28)
Учитывая, что частота соударений в секунду v= 1/т, x = X/v, а при максвелловском распределении скоростей электронов в плазме их средняя квадратичная скорость v—-^JЗкТе/пге, [см. раздел 2.5], получим, разделив обе части на (3/4) kTe:
АТ/Т=(Те — Тл)Те — [ms/(4me)] (ХеєЕ)2/ {(3/2)Щ2<£ 1(2.29)
Здесь ХееЕ — энергия Aw, получаемая электроном от поля на участке пробега Хе, а (3/2) kT — энергия w теплового движения электрона. Для термического равновесия необходимо, чтобы Aw/w и относительная разность температур были значительно меньше единицы. Учитывая, что по формуле (2.11) Х = kT/{pQea) , получим
Aw/wT = eE У [(3/2) £7] =(2/3) (e/Qea)E/p. (2.30)
т. е. Aw определяется в основном отношением Е/р.
Из формул видно, что равновесие легче достигается при малой напряженности поля £, повышенном давлении (малый пробег Хе) и высокой температуре газа.
Для оценки равновесия в столбе различных сварочных дуг рассмотрим следующие примеры:
Пример 1. Приняв для W-дуги в аргоне psslO5 Па, Qea = 2,5- 10~2° м2, Е = 1 • 103 В/м, Х„ = 3- 10~6 м, mk,/me= 105, kT ж 2 эВ, т. е. окло 23 000 К, получим:
2 16- Ю-19 10~3
АшМ=—• -2’5.10-яи --цГ»0-05 (около 5%);
А7_ 1(У (3-»0-М.10»У,
Т ~ 4 [(3/2).2У U, U2o,
т. е. около 2,5%.
Вывод: термическое равновесие в столбе дуги существует.
Пример 2. В плазме вакуумной дуги при давлении р=10Па (около 10“1 мм рт. ст.) в парах железа:
<ЭЙ = 50■ 10-:20 м2 и £= Ш2 В/м.
Расчет по формуле (2.30) дает
. , 2 1,6-10-19 102 оп
Ддо/ш —------- та------ * ~ 2,0,
1 з 50-10 ю
т. е. энергия, получаемая электронами от поля, здесь значительно больше, чем
их термическая энергия, что должно привести к росту электронной температуры.
Действительно, принимая ms/me=104 и учитывая, что X — kT(pQ) при Т ss ж 5800 К; ЛГ = 0,5 эВ = 0,8-10“19 Дж, получим:
а) для р= 105 Па
т. е. пробег мал по сравнению с длиной дуги;
б) для р=ЮПа пробег увеличивается при 7 = const в 104 раз и Хс составляет 2-10-2 м —20 мм, т. е. пробег соизмерим с длиной дуги.
Приняв условно Ге«1,6-105К, кТ х 15, получим по формуле (2.29)
АТ/Т—^1. (2‘ 10“2- 102)2 1 4 [(3/2). 15]2 2
Вывод: в вакуумной дуге термического равновесия нет и электронная температура Те превышает температуру газа Тй в десятки раз.
В дугах низкого давления, а также в переходных зонах дуги, где Е велико, отношение Е/р велико, Дш растет и термическое равновесие нарушается.
КВАЗИНЕЙТРАЛЬНОСТЬ
Всякое разделение зарядов приводит к возникновению электрических полей. Согласно законам электростатики, если на длине г, см, имеется объемный заряд плотностью q, то он создает электрическое поле, которое по уравнению Пуассона равно Е — — Anqr. Пусть в 1 см3 имеется Ап «лишних» электронов сверх тех, которые точно нейтрализуют заряд ионов. Тогда
q = eAn, (2.31)
а £ =4л* 300- 4,8- 10~10Длг лг 2 • 10-6Д/гг. Для воздуха п — = 2,7Х Ю19 молекул или ~5 • 1025 атомов на 1 м3.
Пример 4. Представим, что воздух перевели в состояние плазмы при избыточной ионизации электронов х=1%. Тогда п = 5 • 1023 м“3. Допустим, что на Длинег = 1 см Ап = 1 %. Тогда при Апе = 5 • 1021 м_3 возникает поле Е =2- 10“6Х ХДпег=10'° В/см = 108 В/м и объемная сила f = Еа = 103-5- 1017- 1,6Х Х10“19 = 72- 10“ Н/м
Полученные в расчетах силы в миллион раз больше наблюдаемых, поэтому ясно, что в плотной плазме, где пе= 1022...1024 м~3
(при р^10эПа), разделение зарядов может быть лишь невообразимо ничтожным. Оно становится заметным только при очень малых расстояниях. Для оценки квазинейтральности в физике плазмы установлено понятие временного и пространственного масштабов разделения зарядов. Пространственное разделение измеряется дебаевским радиусом поляризации
|
|
(2.32)
Согласно условию (2.32), если размеры области, занимаемой ионизированным газом с заданной концентрацией п = пе и электронной температурой Те, значительно превосходят rD, то внутри этой области можно считать пе~п,, а если есть многоразрядные ионы с зарядом г,-, то
|
= Пе. |
(2.33)
Это и есть условие квазинейтральности — основное условие, при соблюдении которого скопление заряженных частиц может называться плазмой.
Пример 4. Определим дебаевский радиус поляризации для сварочной высоко - ионизированной плазмы при р=10 Па, Г= 10 ООО К и пе=10|8см_3:
г0<5 /104/1024 м = 5- 10-ш м.
Для данного случая только в кубике газа со стороной меньше 5 им, т. е. только при микромасштабах, можно определить разницу Ап концентрации ионов и электронов.
Вывод: в обычной дуге плазма квазинейтральна.
Пример 5. Проделаем те же расчеты для сварки в вакууме при р=10Па. Примем, как в примере 3, Г, ^160 ООО К, kT = 15 эВ = 25- 10_|э Дж. Тогда /іе = = p/(kT)= 10/(25- 10-19) » 4 ■ 1018 м_3,
rD =5 |qI^ ~5-2 /іО 8= 10-10 4 см = 10 мкм.
Вывод: при сварке в вакууме размер дебаевского радиуса на три порядка меньше размеров столба дуги, поэтому дугу можно считать все еще квази - нейтральной.
ПЛАЗМА КАК ИДЕАЛЬНЫЙ ГАЗ
|
(2.34) |
Известно, что внутренняя энергия идеальных газов не содержит потенциальной энергии взаимодействия между частицами. Идеальный газ — это система частиц, силами притяжения и размерами которых можно пренебречь. Вследствие высоких температур плотность частиц в сварочной плазме, несмотря на сравнительно высокие давления р, настолько мала, что практически часто можно считать справедливыми уравнениями идеального газа, в том числе основной закон газового состояния для 1 моля
pV=RT.
|
(2.35) |
Его удобно записать в виде
p — nkT,
где п — пєПіпо', k = R/N n—N/V # = 8,31 Дж/(мольХ X К) — универсальная газовая постоянная; JV = 6,02- 10 молекул/моль — число Авогадро.
Пример 6. При р = 105 Па из (2.35) получим п = pf(kT) = 7,34 • 1027 (1/71 м_3. Если 7 = 300 К, то п — pj{kT)= 7,34- 1027/ (З -102) ж2,7• 1025 м~3.
Это так называемое число Лошмидта. В плазме дуги на воздухе при р = = 105 Па и Т = 6000 К, несмотря на ионизацию, общее число частиц в 1 см3 уменьшится почти в 20 раз и будет порядка п = р/ (kT) = 1024 м_3.
Отступления от модели идеального газа для плазмы связаны с двумя явлениями, существующими только при больших плотностях: электрическим взаимодействием и так называемым вырождением.
УРАВНЕНИЕ САхХ
Плазму, находящуюся в термическом равновесии, т. е. имеющую практически одинаковую температуру для всех частиц, называют часто термической плазмой. Для нее, как указывалось выше, соблюдаются условия квазинейтральности и, за исключением предельных случаев высокого давления, законы идеальных газов. По виду плазмы сварочные дуги при атмосферном давлении могут быть отнесены к категории дуг термического типа. Можно рассматривать термическую ионизацию, как обратимую химическую реакцию газов:
А+ --е /4°+работа ионизации. (2.36)
Напомним, что степень ионизации — это отношение числа ионизированных частиц (ионов или электронов) в плазме к числу первоначально взятых х= Пі[(па-- ш) = пе/{па-- пе).
Из константы равновесия реакции степень ионизации х определяется уравнением Саха (1921):
[*2/(1 - х2)]р = 2А - 10~4а2Г5/2ехр[ —eUi/(kT), (2.37)
где а2 — gegi/g0 = 2gi/g0 — квантовый коэффициент; *, р, kT, ещ — соответственно степень ионизации газа, его давление, температура и энергия ионизации; g — статистический (квантовый) вес, отвечающий числу возможных состояний частицы с одинаковой энергией. Для электрона ge — 2, что соответствует двум направлениям спина. Для ионов и нейтральных атомов значения gi и g0 вычисляют, исходя из строения атомов.
Значение а2, вычисленное К. К. Хреновым, для различных элементов колеблется в пределах от 1 до 4
|
V |
VI |
VII |
VIII |
|
3/2 |
8/3 |
3 |
4 |
|
Nb |
La |
W |
Th |
|
1 |
1 |
8/5 |
4/3 |
TOC o "1-5" h z для атомов с регулярным строением оболочки Группы периодической системы I II III IV
а................................................... 1 4 1 4/3
для атомов с нерегулярным строением оболочки
Элементы....................................... Сг Мп Fe Си
а2.................................................. 8/7 7/3 12/5 3
Т, К
Рис. 2.18. S-образные кривые степени ионизации различных элементов в зависимости от температуры при атмосферном давлении
Иногда буквой а2 обозначают отношение gi/g. Тогда коэффициент в формуле (2.37) меняется с 2,4 на 3,2.
Кривые зависимости степени ионизации от температуры, вычисленные по уравнению Саха, имеют S-образный вид (рис. 2.18). Например, при атмосферном давлении для калия (и,= = 4,3 В) хх I при 11 ООО К; для водорода («,= 13,5 В) хж 1 при 24 ООО К; для гелия (и, —24,5 В) хлі 1 при 50 ООО К.
Однако надо иметь в виду, что уравнение Саха дает результаты, близкие к опытным, только при малых степенях ионизации
1. При 6000 К расчет по уравнению (2.37) дает для Na х ж0,21; для Аг х«0,23- 10~4. Следовательно, степень ионизации Аг по сравнению с Na меньше в 104 раз.
ЭФФЕКТИВНЫЙ ПОТЕНЦИАЛ ИОНИЗАЦИИ
Так как дуговой разряд существует обычно не в однородном газе, а в смеси газов и паров, находящихся при высокой температуре, то необходимо знание эффективного потенциала ионизации. Практика показывает, что в смеси газов в большей степени ионизируется газ с наименьшим щ. Расчет эффективного потенциала термической ионизации смеси и0 был выполнен
В. В. Фроловым.
|
где для смеси k газов л,- — концентрация 1-го газа в смеси; и,- — потенциал ионизации І-го газа в смеси; Т — температура, К. |
Под и0 смеси, обладающей степенью ионизации х<>, следует понимать потенциал ионизации некоторого однородного газа, в котором (при температуре н общем давлении смеси) число заряженных частиц такое же, как и газовой смеси:
|
|
|
Uo 5800 |
|
Г |
Пример 7. Рассчитать Uo в зависимости от концентрации газовой смеси из паров К и Fe: «к = 4,32 В; uFt= 7,83 В.
|
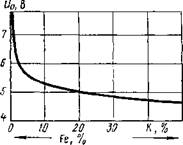
Рис. 2.19. Изменение эффективного потенциала ионизации в системе паров К—Fe |
Предположим, что Т — 5800 К. Тогда
и„=- ПпК^е-^ + ^е-7-83).
Результаты расчета показаны на рис. 2.19.
Следовательно, сравнительно небольшие добавки ионизаторов достаточны для обеспечения стабильности горения дуги при сварке под флюсом или покрытыми электродами.