Уравнения электромеханического переходного процесса электропривода с линейной механической характеристикой при Мс=const и w0=const
В большинстве применяемых в промышленности электроприводов, получающих питание от сети, электромеханические переходные процессы протекают при неизменном напряжении Uя или частоте f1, т. е. при w0=const. Переходные процессы при этих условиях возникают при изменении управляющего воздействия w0 или f1 скачком (пуск, торможение, реверс, отключение от сети) или изменение нагрузки ( скачок нагрузки). Для ограничения тока при пуске или торможении до допустимых значений в цепь якоря или ротора двигателя вводится добавочное сопротивление. При этом электромагнитная постоянная 
силовой цепи значительно снижается, а электромеханическая постоянная Тм, наоборот, увеличивается, т. к. 
, (уменьшается жесткость b). Поэтому при работе двигателя на пусковых характеристиках влиянием электромагнитной инерции на течение переходных процессов можно пренебречь, считая Тэ=0.
Необходимость учета Тэ обычно возникает при выходе двигателя для работы на естественной характеристике, когда добавочные сопротивления полностью выведены и влияние электромагнитной инерции может быть существенным.
Получим уравнения переходного процесса для общего случая при Тэ=0 и ненулевых начальных условиях. Электромеханические переходные процессы при жестких механических связях, т. е. 
, описываются уравнениями
; 
Найдя из второго уравнения М и подставив в первое, получим уравнение, разрешенное относительно w 
Аналогично можно получить уравнение, разрешенное относительно М
Корни характеристического уравнения этих дифференциальных уравнений при 
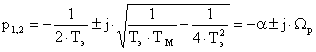
Общее решение этих уравнений при m<4
Постоянные интегрирования A, B, C, D находятся из начальных условий.
При t=0 w=wнач ; M=Mнач ; 
Wнач=wc+A ; Mнач=Мс+С 
Отсюда 
; С=Мнач-Мс ; 
Отсюда 
Т. о. законы изменения w и М будут такими:
При 
корни р1=-a1 ; р2=-a2 и общее решение дифференциальных уравнений относительно w и М имеет вид
Постоянные интегрирования определяются аналогично предыдущему случаю исходя из начальных условий. Законы изменения w и М будут такими:
При 
, что бывает в редких случаях, р1=р2=a и общее решение дифференциальных уравнений относительно w и М имеет вид
Коэффициенты А2, В2, С2, D2 находятся из начальных условий.
Полученные общие зависимости в частных случаях существенно упрощаются, если до начала переходного процесса режим работы электропривода был установившимся.
Во всех случаях, когда двигатель работает на реостатных характеристиках, Тэ пренебрежительно мала и можно считать ее равной 0. Если электромеханическая связь в системе электропривода является жесткой, уравнения переходного процесса можно получить из соотношений для случая m>4, положив в них 
и 
