Математическое описание и электромеханические свойства синхронного двигателя
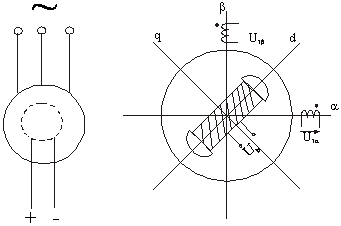Как правило, синхронные двигатели (СД) выполняются с явно выраженными полюсами.
Принципиальная схема и схема двухфазной модели СД изображены на следующих рисунках. Обмотки фаз ее статора питаются симметричной двухфазной системой напряжений.
Обмотка возбуждения расположена на оси d и питается от источника постоянного напряжения.
Уравнения равновесия для цепей статора, ротора и цепи возбуждения в осях α, β, d имеют вид:
а в осях d и q:
Поскольку при работе СД ротор отстает от вращающегося поля на угол 
Наиболее удобной для анализа вид уравнения динамической характеристики имеют в осях d и q. С помощью формул прямого преобразования U1a и U1b к осям d и q
+,0
Подставив это в предыдущую систему уравнений и дополнив ее уравнением эл магнитного момента, получим уравнение динамической характеристики СД в осях d и q.
, т. к. в осях d и q wК=wЭЛ
Соответственно этим уравнениям схема модели СД в осях d и q представлена на рисунке. С учетом того, что для явнополюсной машины 
и в соответствии с этой схемой уравнения потокосцеплений имеют вид:
т. к. магнитные оси обмотки возбуждения и обмотки, расположенной на оси q взаимноперпендикулярны и L12 между ними равна 0.
Эти уравнения нелинейны, поэтому анализ динамических процессов возможен только с применением ЭВМ.
Приближенное уравнение динамических - механических характеристик можно получить с помощью угловой характеристики СД, для получения которой в уравнениях положим
Пренебрежем R1, считаем wЭЛ=w0ЭЛ и считаем, что iB=-IB не меняется во всех режимах работы. Тогда система приобретает вид
Из этих уравнений можно определить токи статора 
Если подставить значения этих токов в уравнение момента, получим уравнение угловой характеристики двухфазного СД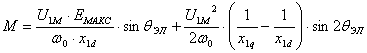 
Заменив переменные двухфазной машины переменными трехфазной машины с помощью формул фазного преобразования и используя действующие значения ЭДС и напряжения, получим известное из курса эл. машин уравнение угловой характеристики СД.
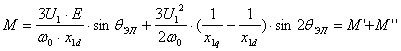
Вторая составляющая момента М – это реактивный момент. Угловая характеристика изображена на следующем рисунке.
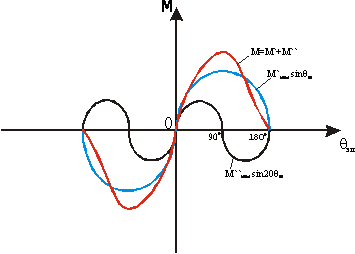Рабочий участок угловой характеристики СД с достаточной для инженерных задач точность можно заменить линейной зависимостью 
,
Где СЭМ коэффициент, характеризующий упругую связь между полем статора и ротора. Дифференцируя, можно получить приближенное уравнение динамической механической характеристики. 
т. к
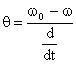
В ранее рассмотренной упругой механической двухмассовой системе момент упругого взаимодействия 
, а 
Т. о. видно, что это уравнение совпадает по форме с уравнением 
Это еще раз подтверждает аналогию между электромагнитными взаимодействиями в СД и механической пружине. Поэтому механическую модель, отражающую особенности СД, можно представить в виде, изображенном на рис.
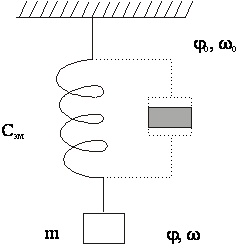Здесь электромагнитная связь между полями статора и ротора СД заменена пружиной с жесткостью СЭМ, а приведенный I ротора и механизма представлен подвешенной на этой пружине массой «m». Очевидно, механический аналог СД представляет собой идеальное колебательное звено, в котором возникающие по тем или иным причинам колебания не затухают.
Реальные СД также подвержены колебаниям при изменении нагрузки и для успокоения этих колебаний в сердечниках полюсов СД устраивается успокоительная (демпферная) к. з. обмотка. При возникновении колебаний (качаний) ротора, т. е. изменении скольжения, она создает асинхронный момент, который в первом приближении можно считать пропорциональным скольжению. С учетом этого результирующий момент СД в динамическом режиме можно представить в виде суммы синхронного и асинхронного моментов.
Т. о. уравнение механической характеристики СД в операторной форме можно записать в виде
, где b - модуль жесткости характеристики для асинхронной составляющей момента, обусловленного действием демпферной обмотки.
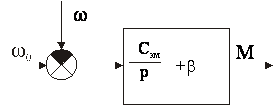Структурная схема синхронного ЭМП, соответствующая этому уравнению, имеет вид. Сравнивая ее со структурной схемой двух массовой механической системы можно установить, что асинхронный момент, создаваемый успокоительной обмоткой, оказывает влияние, аналогичное вязкому трению. Поэтому схема механического аналога СД с учетом наличия успокоительной обмотки должна быть дополнена механическим демпфером с вязким трением, как показано на предыдущей схеме пунктиром.
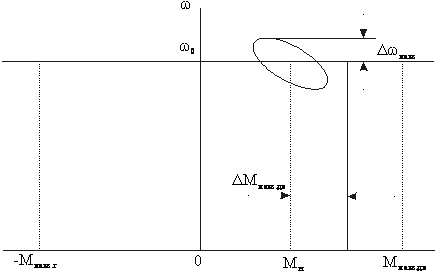
При р=0 получим уравнение статической механической характеристики с w=w0=const при любых значениях М. Действительно из
Выражения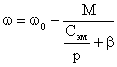 
следует,
Что при р=0 w=0 статическая механическая характеристика имеет вид прямой, параллельной оси моментов в пределах перегрузочной способности двигателя. В динамических режимах, как следует из уравнения момента, механическая характеристика не является абсолютно жесткой. В установившемся динамическом режиме вынужденных колебаний изменениям момента с амплитудой DМmax и соответствующим изменениям угла qэл соответствуют определенные амплитуды Dwmax колебаний скорости и динамическая характеристика имеет вид эллипса. Динамическая жесткость ее определяется соотношением: 
