Движение инерционных масс эл. привода С учетом упругих связей движущихся масс
С целью выявления влияния упругих связей на характер движения инерционных масс эл. привода, проанализируем переходный процесс пуска вхолостую (МС1=МС2=0) электропривода с механической частью в виде двухмассовой упругой системы при приложении к ней скачком электромагнитного момента двигателя М=М1=const. Для получения уравнения движения инерционной массы J 1 воспользуемся передаточной функцией 
, полученной ранее.
Заменив r на 
и считая входным воздействием 
, получим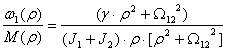 
или т. к. 
разделив на 
, получим
При М=М1=const 
и 
- среднее ускорение.
Корни характеристического уравнения системы с передаточной функцией 
были определены ранее и равны: 
и 
, причем нулевой корень определяет частное решение, соответствующее установившемуся равномерно ускоренному движению системы 
Учитывая это частное решение и то, что корни r2 и r3 мнимые, общее решение приведенного выше дифференциального уравнения имеет вид: 
.
Коэффициенты А и В находятся из начальных условий: В момент t=0 скорость w1 инерционной массы J1 и ее ускорение равны: w1=0; 
, т. к. при определении ускорения инерционной массы J1 инерционную массу J2 нужно считать равной 0.
W1=0=eср 
, отсюда А=0.
;
Отсюда 
; 
.
Следовательно, движение 1-й инерционной массы происходит по закону:
Аналогично полученное уравнение движения инерционной массы J2 имеет вид:
Соответствующее этим двум выражениям кривые 
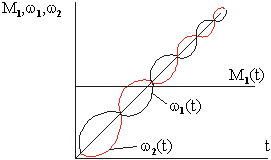
и 
при g<2, изображены на след. Рис.
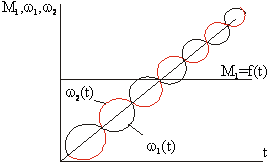
Видно, что переходные процессы в среднем протекают равномерно ускорено, однако мгновенные значения w1 и w2 при этом не совпадают, т. к. содержат колебательные составляющие, причем колебания совершаются в противофазе.
Из последнего уравнения следует, что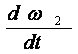 
всегда >0, а для g>0 и 
>0. При прочих равных условиях колебания w1 тем меньше, чем меньшеJ2, а увеличение W12 при тех же ускорениях снижает амплитуды колебаний скоростей w1 и w2.
В реальных системах всегда имеются силы типа внутреннего вязкого трения, поэтому колебания скоростей со временем затухают. Однако, естественное затухание невелико и за время затухания совершается от 10 до 30 колебаний. C учетом вязкого трения, т. е. естественного демпфирования, скорости w1 и w2 изменяются по законам:
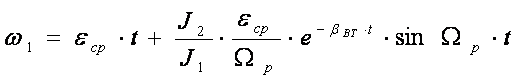
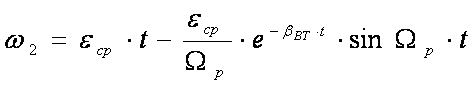, где 
Кривые изменения w1 и w2 изображены на рис.
Упругие колебания в механической части эл. привода неблагоприятно сказываются на его работе, т. к. увеличивают динамические нагрузки, вызывают неравномерность движения, которая снижает точность выполнения технологического процесса.
