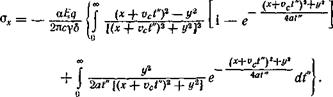СВАРОЧНЫЕ ДЕФОРМАЦИИ И НАПРЯЖЕНИЯ

НАПРЯЖЕНИЯ В БЕСКОНЕЧНОЙ ПЛАСТИНЕ ПРИ НАГРЕВЕ ЕЕ ДВИЖУЩИМСЯ ЛИНЕЙНЫМ ИСТОЧНИКОМ

Определим напряжения в пластине без теплоотдачи при ква - зистационарном температурном поле, которое описывается сле­дующим уравнением [100]:

MS)-

Принимаемые при решении задачи допущения остаются те же, что и в п. 8. Температурное поле движущегося источника склады­вается из множества температурных полей от мгновенных линей­ных источников. Аналогично этому вследствие отсутствия пласти­ческих деформаций поле напряжений также является суммой полей напряжений, возникающих от отдельных мгновенных источ­ников. Для решения поставленной задачи достаточно интегриро­вать эти напряжения (17), (18) при изменении времени t от 0 до оо.

Для этого вначале преобразуем выражения (17) и (18), записав их в декартовых координатах:

X2 + у2.

Интегрирование напряжений проведем на примере ох анало­гично тому, как это сделано при определении температурного поля в работе [100]:

Дифференцируя выражение (24) по а и интегрируя затем по /, получаем

VJL _vj1

10 w (l'cr I y2vce 20 и / V)

2лсу6 L 2aa 0 2a J ' 4a3r Al 2aj.

(25)

Интегрируя выражение (25) по а в пределах от а до оо, находим

SHAPE * MERGEFORMAT

разность ох — ох. Производя вначале подстановку

а затем

[A"o(z) — - у Kt(z)][ =е r К0 (z) dz —

_ X

— (l — ~2-)ге r K1(z)dz,

находим

Впереди источника х > 0; позади к < 0.

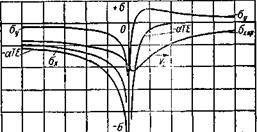
Результаты упругого решения, безусловно, не выражают точ­ных количественных зависимостей напряжений от распределения температур при сварке, однако дают важные представления о ка­чественной картине их распределения. Кроме того, упругое ре­шение в дальнейшем может быть использовано для отыскания упруго-пластического решения задачи и определения зоны пла­стических деформаций и величины усадочного усилия при сварке. По результатам, представленным на рис. 14, интересно отметить, что напряжение ох заметно меньше величины а ТЕ, в особенности

и/>л

при малых значениях безразмерного расстояния, где оно

в jf5—2 раза отличается от напряжений в жестко закрепленном стержне. Это снижение указывает на упругую податливость окру­жающего металла. Напряжения ох в поперечном сечении (рис. 14, (5) также отличаются от эпюры напряжений —а ТЕ, которые воз­никли бы в неподвижно закрепленных волокнах металла.

Еще большее отклонение величины продольных напряжений ох от —а ТЕ наблюдается при нагреве кромки полубесконечной пла-

Рис. 14. Напряжения в упругой пластинє при квазистационарном тем­пературном поле от дви­жущегося линейного ис­точника тепла:

а — по оси движения ис­точника у = 0; ох — про­дольные напряжения в бес­конечной пластине; —по­перечные напряжения в бес­конечной пластине; о». —

лкр

продольные напряжения в полубесконечной пластине при движении источника по краю; — а ТЕ — напряже­ния, пропорциональные тем­пературе при у = 0; б — в поперечном сечении беско - V

нечной пластины при —

2 а

ния, пропорциональные температуре Т, возникающие при жестком закреплении нагретого металла

стины подвижным линейным источником. Для определения на­пряжений ох по краю пластины [1] достаточно разрезать бесконеч­ную пластину на две части по оси и снять напряжения оу. Снятие напряжений оу по краю пластины путем приложения противо­положных по знаку сил дает величину, равную разности напря­жений ох и Оу в формулах (27) и (28) [110]:

Сравнение напряжений ox и —a ТЕ по краю полубесконеч­ной пластины (см. рис. 14, а) убеждает з том, что значительная часть температурной деформации aТ снимается за счет податли-

вости менее нагретого окружающего металла. При х = 0 ох яв­ляется конечной величиной, в то время как —а ТЕ оо.

Температурные напряжения при известном распределении тем­ператур удается определить, как правило, в простейших случаях. Например, определение напряжений в пластине при нагреве ее подвижным линейным источником тепла с учетом теплоотдачи встречает серьезные трудности. В таких случаях целесообразно прибегать к приближенному определению температурных напря­жений при помощи метода, изложенного в п. 11, и цифровых вы­числительных машин (ЦВМ); температурные напряжения в пла­стине могут быть вычислены при любом заданном распределении температуры.