Механические свойства
Нагрузки
Строительные материалы и конструкции подвергаются различным внешним силам — нагрузкам, которые вызывают в них деформации и внутренние напряжения. Нагрузки делятся на статические, действующие постоянно, и динамические, которые прикладываются внезапно и вызывают силы инерции.
На статические нагрузки рассчитываются здания и сооружения промышленного и гражданского строительства. Это нагрузки от оборудования, мебели, людей, самих конструкций и т. д. Ряд сооружений предназначен для восприятия не только статических, но и эксплуатационных динамических нагрузок: мосты, тоннели, дорожные и аэродромные покрытия, кузнечные и прессовые цехи, фортификационные и специальные объекты.
Нагрузки, преимущественно динамического характера, образуются от природных катастроф (землетрясения, ураганы, наводнения, селевые потоки, оползни и др.), а также от аварий на предприятиях (взрывы, удары).
Статические нагрузки действуют независимо от времени, динамические же главным образом зависят от длительности действия: от долей до нескольких секунд, вызывая колебания и смещения сооружений. Ударная волна ядерных взрывов может длиться до 2-3 се
кунд, а интенсивность на ее фронте при этом достигает сотен МПа, вот почему она обладает столь разрушительными последствиями.
Деформации и напряжения
Упругостью твердого тела называют его свойство самопроизвольно восстанавливать первоначальную форму и размеры после прекращения действия внешней силы. Упругая деформация полностью исчезает после прекращения действия внешней силы, поэтому ее принято называть обратимой.
Пластичностью твердого тела называют его свойство изменять форму или размеры под действием внешних сил, не разрушаясь, причем после прекращения действия силы тело не может самопроизвольно восстанавливать свои размеры и форму, и в теле остается некоторая остаточная деформация, называемая пластической деформацией.
Пластическую, или остаточную деформацию, не исчезающую после снятия нагрузки, называют необратимой.
Хрупкостью твердого тела называют его способность разрушаться без образования заметных остаточных деформаций.
Основными характеристиками деформативных свойств строительного материала являются: модуль упругости, коэффициент Пуассона, модуль сдвига, объемный модуль упругости (модуль всестороннего сжатия), предельные деформации (растяжения, сжатия и др.), ползучесть. Другие характеристики могут определяться для специальных условий нагружения.
Рассмотрим связь строения и деформативных свойств материала.
Внешние силы, приложенные к телу, вызывают изменение межатомных расстояний, отчего происходит изменение размеров деформируемого тела на величину Д/ в направлении действия силы (при сжатии — укорочение, при растяжении — удлинение).
Относительная деформация равна отношению абсолютной деформации Д/ к первоначальному линейному размеру / тела:
£ = Д///. (1.18)
Деформация происходит вследствие удаления или сближения атомов, причем смещения атомов пропорциональны деформации тела.
Напряжение — мера внутренних сил, возникающих в деформируемом теле под воздействием внешних сил.
Модуль упругости Е (модуль Юнга)[2] связывает упругую деформацию и одноосное напряжение линейным соотношением, выражающим закон Гука :
є = а/Е. (1.19)
При одноосном растяжении (сжатии) напряжение определяется по формуле сг = Р/F, где Р — действующая сила; F — площадь первоначального поперечного сечения элемента.
Модуль упругости представляет собой меру жесткости материала. Материалы с высокой энергией межатомных связей (они плавятся при высокой температуре) характеризуются и большим модулем упругости (табл. 1.3).
|
Таблица 1.3 Зависимость модуля упругости Е от температуры плавления материала________________________________
|
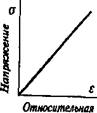
Механические свойства материала характеризуются диаграммой деформаций, построенной на основании результатов испытания в координатах «напряжение - относительная деформация» (а - є).
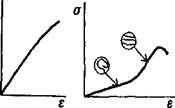
Модуль упругости определяет тангенс угла наклона производной da / ds к оси деформаций. На рис. 1.9 представлены кривые а - є для строительных материалов упругих, пластичных, хрупких и эластомеров.
Стекло деформируется как упругий хрупкий материал (рис. 1.9,а). Поликристаллические изотропные материалы (металлы, кристаллические полимеры и др.) сохраняют упругость при значительных напряжениях; для многих из них характерно пластическое разрушение, отмеченное площадкой текучести A-В на диаграмме а - є (рис. 1.9,6). При хрупком же разрушении пластические деформации невелики (рис. 1.9,в).
Нелинейное соотношение между напряжением и деформацией у некоторых материалов проявляется при относительно невысоких напряжениях. Так, у материалов с конгломератным строением (бетонов различного вида) оно отчетливо наблюдается уже при напряжениях, больших 0,2 предела прочности.
|
|
о) б) в) г)
|
деформация |
Рис. 1.9. Схема диаграмм деформации: а) стекла; 6) стали; в) бетона; г) эластомера
Упругая деформация эластомеров (каучуков) может превышать 100%. Первоначально для распрямления цепей молекул эластомера требуется низкое напряжение. По мере распрямления цепей молекул сопротивление дальнейшему деформированию возрастает, так как увеличение деформаций вызывает разрыв связей уже выпрямленных молекул (рис. 1.9,г).
Таким образом, диаграммы деформаций позволяют определить модуль упругости и установить его изменение в зависимости от уровня напряженного состояния.
Модуль упругости Е связан с другими характеристиками материала посредством коэффициента Пуассона[3]. Одноосное растяжение а, вызовет удлинение по этой оси +е и сжатие по боковым направлениям - ех и ~£у, которые у изотропного материала равны между собой.
Коэффициент Пуассона, или коэффициент поперечного сжатия равен отношению:
fX — —Ех / Еу.
Если бы объем материала при одноосном упругом нагружении оставался постоянным, то наибольшее теоретическое значение ц = 0,5. Силы притяжения и отталкивания в материале различным
образом зависят от изменения межатомного расстояния, поэтому значения коэффициента Пуассона реальных материалов сильно отличаются от теоретического и различаются между собой: у бетона — 0,17-0,2, полиэтилена — 0,4.
Объемный модуль упругости, или модуль всестороннего сжатия (растяжения) К связан с модулем упругости следующим соотношением:
К = £7[з(і-2//)]. (1.20)
Модуль сдвига связан с модулем упругости посредством коэффициента Пуассона:
G = Е /[2(l + //)] (1.21)
Поскольку /2 = 0,2- 0,3, G составляет 35—42% от Е. Используя приведенную выше формулу для К, получим:
G = 3^(1 -2/i)/[2(l + //)]. (1.22)
Экспериментально определив модуль упругости и коэффициент Пуассона, можно вычислить модуль сдвига и объемный модуль упругости, пользуясь приведенными формулами (вывод этих формул дается в курсе сопротивления материалов).
Прочность
Прочность — свойство материалов сопротивляться разрушению под действием внутренних напряжений, вызванных внешними силами или другими факторами (стесненная усадка, неравномерное нагревание и т. п.).
Прочность материала оценивают пределом прочности (временным сопротивлением) R, определенным при данном виде деформации. Для хрупких материалов (природных каменных материалов, бетонов, строительных растворов, кирпича и др.) основной прочностной характеристикой является предел прочности при сжатии. Поскольку строительные материалы неоднородны, то предел прочности определяют как средний результат испытания серии образцов (обычно не менее трех образцов). Форма и размеры образцов, состояние их опорных поверхностей существенно влияют на результаты испытания.
Например, у кубиков малых размеров предел прочности при сжатии оказывается выше, чем у кубиков больших размеров из того же материала. Призмы показывают меньшее сопротивление сжа-
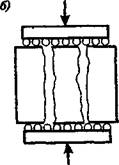
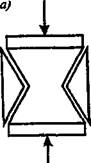
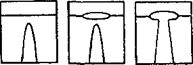
тию, чем кубы одинакового поперечного сечения. Это объясняется тем, что при сжатии образца возникает его поперечное расширение. Силы трения, возникающие между опорными гранями образца и плитами пресса, удерживают части образца, прилегающие к плитам, от поперечного расширения и, следовательно, от разрушения. Средние же части образца, испытывая поперечное расширение, разрушаются в первую очередь. Поэтому при испытании кубов из хрупких материалов (бетона, раствора, камня и Др.) получается характерная форма разрушения: образуются две усеченные пирамидки, сложенные вершинами (рис. 1.10). Если же хорошо смазать опорные грани куба (например, парафином) и тем самым уменьшить силы трения, то под нагрузкой куб вследствие свободного поперечного
|
|
|
Рис. 1.10. Схема разрушения хрупких материалов: а) сжатие куба; 6) то же со смазанными опорными гранями |
|
|
расширения распадается на ряд слоев, разделенных вертикальными трещинами.
При смазке прочность куба при сжатии составляет лишь 50% прочности того же образца с несмазанными поверхностями.
На результаты испытания влияет скорость нагружения образца. Если нагрузка возрастает быстрее, чем установлено стандартом, то результат получается завышенным, так как не успевают развиться пластические деформации.
Чем меньше время нагружения, тем больше напряжения нужно приложить, чтобы материал разрушился. Таким образом, при динамической нагрузке предел прочности оказывается выше, чем при статической, и степень этого превышения зависит от времени и скорости нагружения, и тогда коэффициент динамического упрочнения будет больше единицы:
Кду =-^-. (1.23)
Rem
Приведенные примеры говорят о том, что показатели прочности
строительного материала, используемые в качестве характеристик его качества, являются условными величинами, получаемыми по стандартным методикам, единым для всей страны.
В строительных материалах, работающих в сооружениях, следует допускать напряжения, составляющие только часть предела прочности. Следовательно, допускаемое напряжение:
|
|
(1.24)
где z — запас прочности обычно 2-3 и выше.
В зависимости от прочности строительные материалы разделяются на марки. Марка материала по прочности является важнейшим показателем его качества. В нормативных документах марка указывается в кг/см2; например, марки портландцемента М400, М500, М550 и М600. Чем выше марка, тем выше качество конструкционного строительного материала. Единая шкала марок охватывает все строительные материалы.
|
(1.25) |
Предел прочности при осевом сжатии Ксж (МПа) равен частному от деления разрушающей силы на первоначальную площадь поперечного сечения образца (куба, цилиндра, призмы):
П __ р / Г лслс разр '
В табл. 1.4 систематизированы характерные образцы, применяемые для определения предела прочности строительных материалов при сжатии.
Предел прочности при осевом растяжении Rp (МПа) используется в качестве прочностной характеристики стали, бетона, волокнистых и других материалов (см. табл. 1.4). В зависимости от соотношения Rp / Ясж можно условно разделить материалы на три группы: материалы, у которых Rp > Ясж (волокнистые — древесина и др.); Rp ~ Ясж (сталь); Rp < Rcx (хрупкие материалы — природные камни, бетон, кирпич).
|
(1.26) |
Предел прочности при изгибе (МПа) определяют путем испытания образца материала в виде балочек на двух опорах. Их нагружают одной или двумя сосредоточенными силами до разрушения. Предел прочности условно вычисляют по той же формуле сопротивления материалов, что и напряжение при изгибе:
Rpu =M/W,
где М — изгибающий момент; W — момент сопротивления.
|
Схемы стандартных методов определения ________ прочности______ при сжатии
|
В табл. 1.5 приведены схемы испытания и соответствующие им расчетные формулы. Эти формулы, строго говоря, справедливы в пределах упругой работы материала и при одинаковом его сопротив
лении сжатию и растяжению. Эти условия не выполняются в стадии разрушения материала. При испытании на изгиб кирпича, бетонных балочек разрушение начинается в нижней растянутой зоне, так как эти материалы имеют значительно меньшую прочность при растяжении, чем при сжатии. Поэтому по формулам вычисляют условное значение предела прочности при изгибе, являющееся стандартной прочностной характеристикой кирпича, строительного гипса, цемента, дорожного бетона.
Таблица 1.5
Схемы стандартных методов определения прочности при изгибе и растяжении
|
Размер стандартного образца, см |
|
Расчетная формула |
|
Образец |
|
Схема испытаний |
|
Материал |
Испытание на изгиб
|
Цемент |
|
4x4x16 |
|
1/2 I 1/2 JL * |
|
Призма, кирпич в натуре |
|
ЪР1 2 bh2 |
|
R.. = |
|
Кирпич |
|
12x6,5x25 |
|
т ' т |
|
Бетон |
|
15x15x60 |
|
PI bh2 |
|
Rpu ~ |
|
Призма |
|
Древесина |
|
2x2x30 |
|
Т - Т |
Испытание на растяжение
|
10x10x70 |
|
|
|
Бетон |
|
10x10x40 d = 1 |
|
Стержень, восьмерка, призма |
|
4 Р |
|
Rn = |
|
Сталь |
|
р nd2 |
|
I = 5;l>d |
|
|
|
R Ж рр яШ |
|
Бетон |
|
Цилиндр |
|
d = 15 |
Ударной вязкостью (динамической или ударной прочностью) называют свойство материала сопротивляться разрушению при ударных нагрузках. Она характеризуется количеством работы, затраченной на разрушение стандартного образца, отнесенной к единице объема (Дж/м3) или площади поперечного сечения образца (Дж/м2). Сопротивление удару важно для материалов, используемых при устройстве фундаментов машин, полов промышленных зданий, дорожных покрытий и т. п.
Удельная прочность (коэффициент конструктивного качества) материала равна отношению показателя прочности R (МПа) к относительной плотности (безразмерная величина):
Ry=R/d. (1.27)
Следовательно, это прочность, отнесенная к единице плотности. Лучшие конструктивные материалы имеют высокую прочность при малой собственной плотности.
Для некоторых материалов значения Ry приведены ниже: для
стеклопластика — 450/2 = 225 МПа, древесины (без пороков) — 100/0,5 = 200 МПа, стали высокопрочной — 1000/7,85 = 127 МПа, стали — 390/7,85 = 51 МПа.
Для каменных материалов значения Ry составляют: для легкого
конструкционного бетона — 40/1,8 = 22,2 МПа, тяжелого бетона — 40/2,4 = 16,6 МПа, легкого бетона — 10/0,8 = 12,5 МПа, кирпича — 10/1,8 = 5,56 МПа.
Повышения Ry можно добиться снижением плотности материала или увеличением его прочности.
Теоретическая прочность однородного материала характеризуется напряжением, необходимым для разделения двух примыкающих друг к другу слоев атомов. Теоретическую прочность Rmeop получают из условия, что в момент разрушения вся энергия упругой деформации, накопленная в объеме между двумя слоями атомов, переходит в поверхностную энергию двух вновь образовавшихся при разрушении поверхностей:
RmeoP =л[ЕЭ/а, (1.28)
где Е — модуль упругости; Э — поверхностная энергия твердого тела на 1 см2, а — межатомное расстояние (в среднем 2-І О'8 см).
Теоретическая прочность материала тем выше, чем больше модуль упругости и поверхностная энергия и чем меньше межатомное расстояние.
Согласно приведенному выражению прочность твердого тела
43
должна находиться между значениями Е/5 и £710. Например, теоретическая прочность стали 30 ООО МПа, в то время как прочность обычной стали около 400 МПа, а специальной проволоки — 3000 МПа. Теоретическая прочность стекла при комнатной температуре — 14 000 МПа, прочность на растяжение тонких стеклянных волокон (толщиной 3-5 мкм) — 3500-5000 МПа, а обыкновенного стекла — только 70-150 МПа. Используется сравнительно небольшая доля потенциальной прочности материала: прочность понижается благодаря наличию пор, трещин и дефектов структуры материала.
Влияние строения на прочность
Прочность материала одного и того же состава зависит от его пористости. На рис. 1.11 представлен график прочности цементного бетона, показывающий, что увеличение пористости с 12,4 до 15,2% снизило прочность при сжатии с 37,5 до 26 МПа. Подобная зависимость характерна и для других материалов (известняка, керамических материалов и пр.).
|
40 |
|
|
IS 8* 30 |
|
|
if |
|
|
<!§ |
20 |
|
<Г |
10 |
|
12 13 14 15 Пористость бетона, *А 1.11. Кривая зависимости прочности цементного бетона от пористости |
|
Рис. |
Реальные кристаллические материалы имеют большее или меньшее количество точечных дефектов. Одни из них заключаются в том, что некоторые атомы или ионы смещены в другие положения и могут располагаться даже между узлами кристаллической решетки. Их нормальные места остаются свободными и затем замещаются другими ионами. Следовательно, в узлах решетки могут быть свободные места (вакансии). Другого рода дефекты возникают в результате размещения посторонних атомов или ионов примеси в узлах решетки, где они заменяют основное вещество (примеси замещения), или между ними (примеси внедрения).
Свойства кристаллических материалов зависят от дислокаций кристаллов.
Дислокация — это всегда одномерный (линейный) дефект кристаллической решетки, возникающий или в процессе образования кристалла, или в результате последующих механических, тепловых и
других воздействий. Дислокации бывают краевые, винтовые и смешанные — криволинейные.
|
|
1 На рис. 1.12 схематически
|
/ |
|||||||
|
4 |
|||||||
|
/ |
/ |
||||||
|
— |
— |
— |
'Х7 |
Г |
... |
||
|
/ |
|||||||
|
Рис. 1.12. Кривая дислокация в кристаллической решетке: / —экстраплоскость |
изображена краевая дислокация. Отклонение от идеального строения кристалла вызвано тем, что один слой атомов (он расположен на рисунке в экстраплоскости) по каким-то причинам оказался незавершенным. Кромка 1-Г «лишнего» слоя атомов образует линейный дефект, называемый краевой дислокацией (она обозначена на рис. 1.12 знаком д.). По обе стороны от кромки экстраплоско-
SHAPE * MERGEFORMAT

|
і А______ |
1 |
||||
|
3 |
J |
4 |
S |
*1 |
|
|
Г |
г |
г |
в' |
||
|
Рис. 1.13. Схема пластического сдвига путем движения дислокации |
сти атомы сдвинуты на угол, соответствующий теоретической плоскости кристалла на сдвиг. Стоит приложить внешнее усилие, значительно меньшее теоретической прочности данного кристалла, чтобы осуществить сдвиг на одно межатомное расстояние в плоскости А-А, нормальной к экстраплоскости (рис. 1.13).
Продолжая нагружать кристалл, перемещаем дислокацию из одного
|
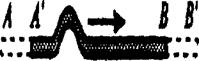
Рис. 1.14. Складка ковра в качестве модели скольжения: АА'-ВВ' — перемещение ковра |
ряда атомов в другой, пока не вытолкнем дислокацию на грань кристалла. Механизм скольжения, основанный на движении дислокации, может быть сопоставлен с перемещением по полу ковра с предварительно созданной складкой (рис. 1.14). При таком способе требуется значительно меньшее усилие, чем в случае перемещения ковра как единого целого.
Дислокационная теория рассматривает пластический сдвиг в 45
кристаллических материалах как скольжение путем движения дислокации. Подвижность дислокации зависит от того, насколько легко межатомная связь может быть разрушена и вновь восстановлена; ведь каждый раз, когда дислокация перемещается на один шаг (межатомное расстояние), должны рваться старые связи и устанавливаться новые. В этом отношении предпочтительнее связи, обеспечивающие одинаковое притяжение во всех направлениях: металлическая и ионная. Дислокации в ковалентных кристаллах при нормальной температуре малоподвижны, так как ковалентная связь является направленной, наиболее прочной и жесткой.
Дислокации присутствуют почти во всех кристаллических материалах. Они значительно понижают прочность монокристаллов, но зато придают пластичность поликристаллическим телам с металлической связью, делают металл ковким, затрудняют распространение трещин. Теоретическая прочность железа на сдвиг около 7000 МПа, но практически кристалл очень чистого железа сдвигается при напряжении, меньшем в 1000 раз, — около 7 МПа; для рядовых сталей прочность на сдвиг 150-250 МПа, для высокопрочных 1500 МПа. Доказательством, подтверждающим объяснение низкой прочности кристаллов движением дислокаций, являются результаты изучения механических свойств «усов». Эти нитевидные кристаллы различных материалов, выращенные без краевых дислокаций, способны претерпевать упругую деформацию до 5-6% без признаков пластического течения. Бездислокационные «усы» способны выдержать напряжения сдвига, достигающие 5% от модуля сдвига; это на несколько порядков больше, чем у обычных кристаллов. В реальности дислокаций убеждают и непосредственные наблюдения. Те места, где дислокации выходят на поверхность, выявляются с помощью химического травления в виде «оспинок»-ямок травления.
Плотность дислокаций (т. е. число дислокаций, пересекающих площадь в 1 см2) может быть весьма велика — 107-108 (в отожженных металлах). При механических воздействиях дислокации перемещаются, взаимодействуют между собой и порождают новые дислокации, в особенности в местах концентрации напряжений. В результате этого их плотность возрастает до Ю10—1013 (в сильно наклепанных металлах). Когда дислокаций много (больше некоторой критической плотности), они переплетаются (словно спутанные нитки), тормозят перемещение друг друга, в результате материал упрочняется. Однако при дальнейшем деформировании материал может сделаться хрупким.
Вакансии в кристаллической решетке, межузловые (внедренные)
атомы, дислокации играют важную роль в процессах диффузии, повышают химическую активность, что используется, в частности, в технологии быстротвердеющих цементов. Однако наличие дислокаций и дефектов структуры в готовом материале снижает его стойкость, так как деформированные межатомные связи (как и места концентрации напряжений) более уязвимы для химических и физических воздействий среды. Следовательно, дислокации следует рассматривать как структурный фактор, регулирующий комплекс наиболее важных свойств кристаллических материалов.
Механика разрушения
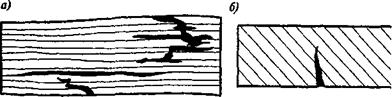
Различают хрупкое и пластическое разрушение твердых тел. Хрупкое разрушение сопровождается малой предшествующей пластической деформацией, поэтому хрупкость определяют как свойство материала разрушаться «внезапно», не претерпевая существенной деформации. Хрупкость присуща не только кристаллическим, но и стеклообразным и даже полимерным материалам.
Разрушению пластичных (вязких) материалов предшествуют изменение формы и большая деформация.
Большинство материалов при понижении температуры становятся хрупкими. У них наблюдается переход от пластического вида разрушения к хрупкому. Так ведут себя битумные материалы, некоторые полимеры, металлы и др.
|
Рис. 1.15. Концентрация напряжений в пластине с трещиной |
Хрупкое разрушение происходит в результате образования и быстрого роста одной или нескольких трещин при возрастающей нагрузке.
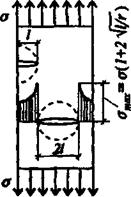
Трещина (как и надрез) вызывает концентрацию напряжений около ее вершины (рис.
1.15). В этом месте напряжение оказывается значительно большим, чем можно ожидать из простого уменьшения площади поперечного сечения.
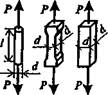
Напряжение о на конце трещины зависит от номинального напряжения о„, длины (глубины) трещины 1 и радиуса кривизны в вершине трещины г.
ак =<т(і + 2 V//r) (1-29)
Коэффициент концентрации напряжений ак =o-(l + 2‘JTTr) может быть равен 100 и даже 1000, если радиус вершины трещины соизмерим с радиусом атома, хотя глубина трещины лишь 0,1 и 10 мкм. Следовательно, местное напряжение может превысить 7000 МПа при номинальном (т. е. среднем по сечению) напряжении 35-100 МПа. Трещина как бы разрезает атомные цепочки, и значительная часть нагрузки, которую несли разрезанные атомные цепочки, приходится теперь на атомную связь у конца трещины. Перегруженная связь лопнет раньше других и положение ухудшится, так как следующее звено будет еще больше перегружено. Таким образом, трещина становится тем инструментом, с помощью которого приложенная извне слабая сила рвет прочные межатомные связи.
При распространении трещины материал вблизи трещины разгружается, и вследствие этого выделяется энергия деформации. Объем, в котором выделяется энергия, изображается на рис. 1.15 как половина объема цилиндра единичной высоты, численно равного тй1 /2 . Выделенная энергия Uд зависит от приложенного напряжения сг, модуля упругости Е и глубины трещины / (половина длины внутренней трещины);
Образование двух новых поверхностей трещины требует затрат энергии
U п = 23,/, (1.31)
где З, — поверхностная энергия единицы площади поверхности.
Трещина будет самопроизвольно расти, если длина трещины превышает некоторую «критическую длину Гриффитса» , при которой освобождающаяся энергия упругой деформации больше энергии образующихся новых поверхностей, тогда
тйаг1Е = 2Эх, (1.32)
откуда
а = (2ЭгЕ/лі)1^2. (1.33)
Напряжение, необходимое для разрушения растянутой пластины, возрастает у материалов с высоким модулем упругости и боль
шей поверхностной энергией, оно уменьшается при наличии более глубоких поверхностных трещин.
В данном материале для каждого напряжения существует своя критическая длина трещин. Трещины, глубина которых превышает 1кр, способны при данном напряжении а самопроизвольно расти со скоростью, приближающейся к скорости распространения упругой волны (1,5-2 км/с).
Сжимающие усилия в отличие от растягивающих могут передаваться через трещины, не вызывая концентрации напряжений. Поэтому хрупкие материалы всегда оказываются значительно прочнее при сжатии, чем при растяжении. Например, у природных каменных материалов (гранит и др.) предел прочности при растяжении составляет всего 1/40-1/60 предела прочности при сжатии. Хрупкие материалы также плохо сопротивляются удару и взрыву.
Торможение трещин при помощи создаваемых в материале внутренних поверхностей раздела используется в современных композиционных материалах.
Механизм торможения трещины основан на том, что при распространении трещины кроме напряжений, перпендикулярных трещине, достигающих максимума в ее вершине, возникает растяжение в направлении, параллельном трещине. Растягивающее напряжение, параллельное трещине, равно нулю в вершине трещины и достигает максимума впереди трещины на расстоянии одного-двух атомных размеров от ее вершины. В растянутом материале отношение максимального напряжения, параллельного трещине, к максимальному напряжению, направленному перпендикулярно ее поверхности, равно приблизительно 1/5. Если прочность сцепления на поверхности раздела больше 1/5 прочности материала, то поверхность не разрушится, трещина ее только пересечет и поведение материала не изменится, т. е. он останется хрупким. Если же прочность сцепления меньше 1/5 прочности на растяжение самого материала, то, прежде чем трещина достигнет поверхности раздела, последняя будет разрушена на небольшом участке и образуется ловушка, способная остановить трещину (рис. 1.16).
|
|
Кончик трещины, который был очень малым, при встрече с поверхностью раздела становится очень большим, устраняется концентрация напряжений в вершине трещины и тенденция к ее распространению Рис. 1.16. Схема торможения трещин (рис. 1.17).
|
Рис. 1.17. Влияние внутренних поверхностей на торможение трещин: а) волокнистый материал, содержащий внутренние поверхности; 6) однородный материал |
|
Модели механических свойств |
|
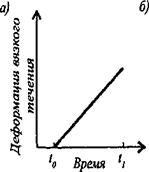
Механические свойства материалов моделируют, используя реологические факторы: упругость, пластичность и вязкость. Реология — наука о деформациях и текучести вещества, исследующая различные деформации материалов в зависимости от напряжений и времени. Вязкость — способность материала поглощать механическую энергию при деформации образца. Для моделирования поведения упругого материала используют пружину. Упругая деформация идеального тела возникает тотчас после приложения силы и не зависит от времени, как это показано на рис. 1.18. После снятия нагрузки деформация становится равной нулю, следовательно, деформация упругого твердого тела постоянна и обратима. Идеальная (ньютоновская) жидкость подчиняется уравнению вязкого течения £еЯш=т1/т1> (1.34-) где т — напряжение сдвига (Па); t — время (с); т] — вязкость (Па с). Деформация вязкого течения при постоянном напряжении сдвига возрастает пропорционально времени (рис. 1.19,а). Поведение жидкости моделируют демпфером (рис. 1.19,6), в котором поршень перемещается под действием приложенных сил, при этом жидкость протекает через кольцевой зазор между стенками цилиндра и поршнем. |
|
|
|
й) 3 |
|
І |
|
і * |
|
I, |
|
t |
|
I |
|
Рис. 1.18. Модель идеального (подчиняющегося закону Гука) твердого тела: а) график упругой деформации; б) модель-пружина |
|
|
|
Рис. 1.19. Модель идеальной (ньютоновской) жидкости: а) график деформации вязкого течения; б) модель-демпфер |
|
а) |
|
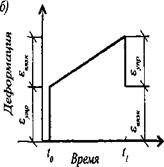
Рис. 1.20. Сочетание упругих и вязких свойств: а) упругий и вязкий элементы расположены последовательно (модель Максвелла); б) график упруго-вязких деформаций |
Поведение материалов, сочетающих упругие и вязкие свойства, можно описать с помощью модели Максвелла*, состоящей из пружины и демпфера, соединенных последовательно (рис. 1.20,а) при постоянном напряжении. В первый момент времени t0 сопротивление создается упругим элементом и возникает упругая деформация £упр, сохраняющаяся неизменной при постоянном напряжении. В
период времени от t0 до /, деформация возрастает вследствие вязкого течения (оно моделируется демпфером, присоединенным к пружине). В момент времени tx при снятии нагрузки упругая составляющая деформации равна нулю, но вязкое смещение ееяж сохраняется, так как оно необратимо. Следовательно, общая деформация є асфальтобетона, пластика и т. п. содержит упругую и вязкую составляющую :
^ £ упр ^вязк
В соответствии с законом Гука и приведенной выше формулой для £вязк получаем следующее уравнение упруго-вязкой деформации:
Д. Максвелл (1831-1879) — английский физик, создатель классической электродинамики.
|
(1.35) (1.36) |
|
є = а / Е + at / tj, є = сг(1 / E + t / 77). |
Соответствующий график приведен на рис. 1.20, б. Примером вязкого течения является след шин, вдавившихся в асфальтовое покрытие дороги. Он напоминает о повышенной склонности к вязкому течению материала покрытия в жаркую погоду. При высокой температуре вязкое течение проявляется у стекла, металла и других твердых материалов.
Релаксация напряжений
Релаксация — свойство материала самопроизвольно снижать напряжения при условии, что начальная величина деформации остается неизменной.
Модели деформации твердых тел дают возможность получить количественную характеристику скорости релаксационных явлений, протекающих в полимерных и других строительных материалах. Если быстро деформировать тело (например, полимер), сохраняя деформацию постоянной, то напряжение постепенно уменьшается. Деформация вызывает перестройку внутренней структуры тела, и требуется некоторый промежуток времени, пока все частицы тела придут в равновесие в соответствии с новыми условиями.
Элементарная модель релаксации напряжений при постоянной деформации представляет собой последовательное соединение пружины и демпфера (модель Максвелла). Для этой модели общая деформация є равна сумме упругой и вязкой составляющих (см. рис.
|
(1.37) |
1.20)
& ^упр «Я1 к Const.
Следовательно,
|
(1.38) (1.39) |
упр dt £вязк / dt •
Поскольку Еупр = а! Е, а £вязк = - at /77, получим {do / А)- (і / Е) = - о / т],
вязк
откуда
|
(1.40) |
da Е
— = dt.
а 77
Введем постоянную времени релаксации Я = 77 / Е, тогда
|
|
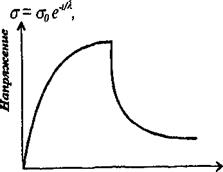
где а — напряжение по прошествии времени t; <т0 — первоначальное напряжение. Из формулы видно, что релаксация напряжения следует экспоненциальному закону (рис. 1.21). Скорость релаксации напряжения характеризуется временем релаксации — промежутком времени, в течение которого напряжение уменьшается в е раз по сравнению с первоначальным (где е — основание натуральных логарифмов).
|
Время Рис. 1.21. Релаксация напряжений по постоянной деформации |
Деформативные свойства материалов зависят от температуры. При нагревании они размягчаются и переходят в пиропластическое (глина, стекло и др.) или каучукоподобное (линейные полимеры) состояние, затем плавятся и становятся жидкотекучими.
Следовательно, в зависимости от температуры материал может проявлять упругие, вязкоупругие и вязкие свойства.
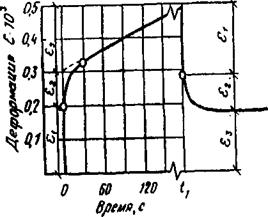
Для анализа деформаций материалов в температурном интервале, охватывающем эти три состояния, может быть использована модель, включающая три элемента: 1 — упругий; 2 — вязкоупругий; 3 — вязкий (рис. 1.22,а). Полная деформация этой модели равна сумме деформации каждого последовательно расположенного элемента:
£ — £| ~h £2 .
Поскольку каждый элемент модели функционирует раздельно, он характеризуется своими значениями £ и 77, поэтому
е = а/Ех +а/E2(l-e~tE^r,2) + ot/т]ъ. (1-42)
На рис. 1.22, б представлено развитие деформации во времени. После прекращения действия напряжения, начиная с момента времени, упругая г, и вязкоупругая е2 составляющие деформации становятся равными нулю, а вязкая деформация £3 необратима.
I
|
Рис. 1.22. Модель вязкоупругости: а) модель деформаций; 1 — упругий элемент; 2 — вязкоупругий элемент (реологическое тело Кельвина ); 3 — вязкий элемент; б) реологическая кривая развития деформации во времени |
Твердость, истираемость, износ
Твердостью называют свойство материала сопротивляться проникновению в него другого более твердого тела. Твердость природных каменных материалов оценивают шкалой Мооса, представленной десятью минералами, из которых каждый последующий своим острым концом царапает все предыдущие. Эта шкала включает минералы в порядке возрастающей твердости от 1 до 10:
1. Тальк Mg3 [Si4Oio][OH]2 — легко царапается ногтем.
2. Гипс CaS042H20 — царапается ногтем.
3. Кальцит СаС03 — легко царапается стальным ножом.
4. Флюорит (плавиковый шпат) CaF2 — царапается стальным ножом под небольшим нажимом.
* У. Кельвин (1824-1907) — лорд, титул, полученный английским физиком У. Томсоном за научные открытия.
5. Апатит Ca5[PC>4]3F — царапается ножом под сильным нажимом.
6. Ортоклаз K[AlSi308]
7. Кварц Si02
8. Топаз Al2[Si04][F,0H]2
9. Корунд А1203
10. Алмаз С
— легко царапают стекло, применяются в качестве абразивных (истирающих и шлифующих) материалов.
Твердость древесины, металлов, бетона и некоторых других строительных материалов определяют, вдавливая в них стальной шарик или твердый наконечник (в виде конуса или пирамиды). В результате испытания вычисляют число твердости НВ = P/F, где F — площадь поверхности отпечатка.
От твердости материалов зависит их истираемость: чем выше твердость, тем меньше истираемость.
Истираемость оценивают потерей первоначальной массы образца материала, отнесенной к площади поверхности истирания, и вычисляют по формуле (г/см2)
И = (тх - m2)lF, (1.43)
где /и, и т2 — масса образца до и после истирания.
Сопротивление материала истиранию определяют, пользуясь стандартными методами: кругом истирания и абразивами (кварцевыми песком и наждаком). Это свойство важно для эксплуатации дорог, полов, ступеней лестницы и т. п.
Износом называют свойство материала сопротивляться одновременному воздействию истирания и ударов. Износ определяют на образцах материалов, которые испытывают во вращающемся барабане со стальными шарами или без них. Показателем износа служит потеря массы пробы материала в результате проведенного испытания (в % от первоначальной массы).
Вопросы для самоконтроля
1. Какие существуют методы оценки для определения структуры материалов на микроуровне?
2. Каковы числовые значения и размерности истинной и средней плотности, пористости, коэффициента плотности, теплопроводности и теплоемкости для тяжелого и ячеистого бетона, керамического кирпича и древесины?
3. Каковы числовые значения прочности при сжатии, изгибе и растяжении с указанием размерности для тяжелого и ячеистого бетона, керамического кирпича и древесины?
4. Какие формы образцов и схемы испытаний используются для определения прочности материалов при сжатии, изгибе, растяжении?
5. Какие деформации в координатах напряжение-деформации показывают материалы упругие, пластичные, хрупкие?
6. Как можно моделировать механические свойства материалов?