Современные светодиоды

Распределенные зеркала Брэгга

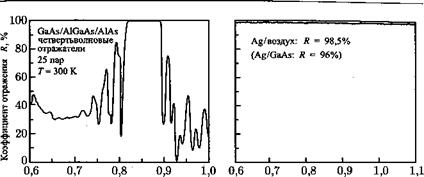
На рис. 10.6 для сравнения приведены спектры коэффициента от­ражения двух типов, отражателей: зеркала Брэгга и металлического зеркала. Видно, что металлические отражатели имеют широкую полосу с высоким коэффициентом отражения, тогда как для зеркал Брэг­га характерен узкий диапазон с высоким коэффициентом отражения, называемый полоса затухания. Следует отметить, что отражательная способность металлических зеркал остается всегда неизменной, тогда

как коэффициент отражения зеркал Брэгга растет по мере увеличения количества двойных слоев пока эти слои полностью прозрачны.

У светодиодов, выращенных на непрозрачных подложках, 50% из­лучения из активной области поглощается именно подложкой, что приводит к существенному снижению их эффективности. Поглощения излучения в подложке можно избежать, если между ней и активной областью светодиода поместить зеркало, отражающее лучи, испуска­емые активной областью в сторону подложки, позволяя им покинуть полупроводник через верхнюю границу.

Для этих целей хорошо подходят распределенные зеркала Брэгга (DBRs). На рис. 10.7 показана структура светодиода с зеркалами Брэг­га. Описание такого светодиода, реализованного на системе материалов AlGaAs/GaAs, было впервые дано Като и др. (Kato et al., 1991). В состав данного диода, излучающего в инфракрасной области спектра на длине волны 870 нм, входило зеркало Брэгга, состоящее из 25 пар слоев AlAs/GaAs или AlGaAs/GaAs.

Распределенное зеркало Брэгга является многослойным отражате­лем, обычно состоящим из 5-50 двойных слоев материалов с разными показателями преломления. Из-за разницы показателей преломления на каждой границе раздела двух материалов происходит отражение Френеля. Но поскольку эта разница обычно не очень большая, от­ражение Френеля на каждой из границ невелико. Однако в состав зеркала Брэгга входит много таких границ. Очень важно так подобрать толщину двойных слоев, чтобы при сложении всех отраженных волн появлялась конструктивная интерференция. Для лучей, падающих на границы раздела под углом 90°, условие резонанса наступает тогда, когда толщина слоев, составляющих пары, равна четверти длины волны света, т. е. при нормальном падении лучей на границу раздела:

ti, h = -Ч/г/4 = Ао/ (4п(,ь). (10.10)

Здесь Ао — длина волны Брэгга в вакууме, t^h — толщина слоев с высо­ким (К) и низким (і) показателями преломления, — показатель пре­ломления материалов с высоким (h) и низким (I) показателями прелом­ления. Толщина реального слоя, определяемая выражением (10.10), не обязательно должна составлять А/4, она может быть равна величине, кратной А/4, но при этом необходимо, чтобы степень кратности была любым нечетным числом, т. е. t^h = А/4, ЗА/4, 5А/4, 7А/4, Толщина слоев определяет усиление интерференции отраженных волн. Однако следует помнить, что при слоях толще А/4, например ЗА/4, будет происходить сужение полосы затухания с высоким коэффициентом отражения.

Для углов падения, отличных от прямого, волновой вектор может быть разделен на параллельную и нормальную составляющие. Как и в случае нормального падения лучей, толщина слоев, составляющих зеркало Брэгга, должна быть равна четверти длины волны нормальной составляющей волнового вектора. При произвольном угле падения лу­чей Oi'h. (не равном прямому углу) для получения высокой отражатель­ной способности зеркала Брэгга оптимальную толщину слоев следует выбирать исходя из следующего соотношения:

ti, h = Aj, k/(4cos0j,/») = А0/ (4niih cos di'h)- (10.11)

Здесь, как и в предыдущем случае, толщина реального слоя может быть равна величине, рассчитанной по формуле (10.11) и умноженной на любое нечетное, число. Отражательная способность зеркал Брэгга с достаточно большим количеством четвертьволновых слоев может быть близка к 100%.

При размещении в светодиоде зеркала Брэгга необходимо вы­полнять следующие условия. Во-первых, поскольку двойная гетеро­структура светодиода обычно выращивается сверху зеркала Брэгга, для предотвращения появления дислокаций несоответствия параметры кристаллических решеток зеркала и гетероструктуры должны быть согласованы. Во-вторых, для получения высокого коэффициента от­ражения зеркал Брэгга при невысоком коэффициенте контраста его слоев необходимо, чтобы все слои зеркала Брэгга были прозрачными для излучения рабочих длин волн. В случае двойных слоев с боль­шой разницей в показателях преломления (например Si/SiC^) зеркало Брэгга будет обладать высоким коэффициентом отражения, даже если один из материалов пары слегка поглощает излучение интересующей длины волны. В-третьих, если зеркало Брэгга расположено в области протекания тока, его слои должны изготавливаться из проводящих материалов.

На рис. 10.8 показаны зависимости коэффициентов отражения зер­кал Брэгга на основе Si/Si02 и AlAs/GaAs от длины волны излучения. Длина волны Брэгга соответствует центру полосы с высокой отража­тельной способностью или полосе затухания. Из рис. 10.8 видно:

— отражательная способность зеркала Брэгга Si/SiC>2 с высоким коэффициентом контраста намного выше, чем у отражателя AlAs/GaAs с низким коэффициентом контраста (при одинаковом количестве четвертьволновых слоев);

— ширина полосы затухания зеркала с высоким коэффициентом кон­траста намного больше ширины этой области у зеркала с низким коэффициентом контраста.

Характеристики зеркал Брэгга Обычно рассчитывают при помощи соответствующих матриц методами матричной алгебры (Born, Wolf, 1989). Более подробно зеркала Брэгга рассмотрены в работах Колдрена и Корзина, Ярива и Бьерка и др. (Coldren, Corzine, 1995; Yariv, 1989; Bjork et al., 1995). Ниже приведен краткий конспект расчета парамет­ров зеркал Брэгга.

Рассмотрим распределенное зеркало Брэгга, состоящее из т двой­ных диэлектрических слоев с коэффициентами преломления Щи, где индексы I и h соответствуют идеальным материалам без потерь с высоким (К) и низким (I) показателями преломления. Считается, что толщина слоев, составляющих пары, равна четверти длины волны, т. е Li'h = ABragg/(471;^). Период зеркала Брэгга равен Li + Lh. Ко­эффициент отражения от одной поверхности раздела двух сред при нормальном падении лучей определяется уравнением Френеля

г=пд-пі (1012)

rih + ni

Многократные отражения от поверхностей раздела в зеркале Брэгга и усиливающая интерференция множества отраженных лучей приводят к повышению отражательной способности, пропорциональной увели­чению числа двойных слоев. На длине волны Брэгга наблюдается максимальный коэффициент отражения, который для зеркала из т

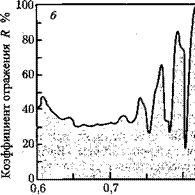
Рис. 10.8. Зависимости отражательных способностей двух распределенных зеркал Брэгга от длины волны излучения: а —для зеркала Брэгга на основе Si/SiCb с высоким коэффициентом контраста, состоящего из четырех двойных слоев, б—для зеркала Брэгга на основе AlAs/GaAs, состоящего из 25 двойных слоев. Для достижения высокой отражательной способности зеркалу с высо­ким коэффициентом контраста требуется только четыре двойных слоя. При этом полоса затухания зеркала Брэгга с высоким коэффициентом контраста намного шире, чем у зеркала с низким коэффициентом контраста

четвертьволновых слоев находится из выражения (Coldren, Corzine,

1995)

Ширина полосы затухания зеркала Брэгга зависит от разно­сти показателей преломления двух материалов, составляющих пару: nh — ni = Дп. Спектральная ширина полосы затухания определяется

выражением (Yariv, 1989)

2A]3ragg ' Аії neff

где neff — эффективный показатель преломления зеркала Брэгга. Для эффективной работы светодиода ширина полосы затухания должна быть больше ширины спектра излучения активной области.

Эффективный показатель преломления зеркала Брэгга можно вы­числить при помощи выражения

(10.15)

В случае небольшой разницы в показателях преломления слоев, например Дп <С Ащ, эффективный показатель преломления может быть рассчитан по приближенной формуле

пе ft = 2 (ni+nh).

Оптическая волна проникает в зеркало Брэгга на ограниченное расстояние, равное конечному числу четвертьволновых слоев. Именно это эффективное число двойных слоев из общего количества четверть­волновых слоев эффективно отражает волну. В работе Колдрена и Корзина (Coldren, Corzine, 1995) приведено выражение для его оценки:

(10.17)

Для толстых зеркал Брэгга (то —> оо) функция th стремится к единице, поэтому выражение (10.17) можно упростить:

На брэгговской длине волны (А = Asragg) изменение фазы отра­женной волны равно нулю, а в ее окрестности (А яз Asragg) фаза отраженной волны связана с длиной волны линейной зависимостью. Поэтому зеркало Брэгга можно схематично представить в виде иде­ального металлического отражателя, расположенного на расстоянии Lpen от поверхности первого двойного слоя зеркала Брэгга (рис. 10.9). Тогда для вычисления коэффициента отражения зеркала Брэгга можно воспользоваться соотношением

tdbr « tdbr ■ e 2І(/3 /3BrasB)'Lpc",

' ^ре:

=£ре:

Рис. 10.9. Иллюстрация глубины проникновения оптической волны внутрь зеркала Брэгга: а — зеркало Брэгга, состоящее из двух материалов толщины L и L?, б —идеальный металлический отражатель, размещенный на расстоянии глубины проникновения от поверхности зеркала Брэгга

где /3 = 27г/Л — средняя фазовая постоянная волны. Изменение фазы волны, отраженной от металлического отражателя при z = 0 определя­ется показателем выражения (см. рис. 10.9):

Гтеіг =Кеы-е2г(2”/Х>^. (10.20)

2=0

Приравнивая изменения фаз, определяемые показателями в уравнени­ях (10.19) и (10.20), и используя формулу для фазовых изменений в зеркалах Брэгга (Coldren, Corzine, 1995), можно найти глубину проникновения оптической волны:

ipen = Ll^L2 • th(2mr). (10.21)

При большом числе двойных слоев (т —у оо), глубина проникновения определяется выражением

L -(- Z/2 L + L/2 Пі + ТІ2

4 г 4 пі — n2 ’

На основе выражений (10.22) и (10.18) можно вывести следующую формулу:

£реп —^ 2meff • (Li + Li)- (10.23)

Коэффициент 1/2 в выражении (10.23) появляется из-за того, что тек соответствует эффективному числу периодов напряженности электри­ческого поля, тогда как Lpen соотносится с оптической мощностью. Поскольку оптическая мощность пропорциональна квадрату напряжен­
ности электрического поля, оптическое излучение проникает в зеркало на глубину в два раза меньшую, чем электрическое поле. Поэтому эффективная длина резонатора, состоящего из двух зеркал Брэгга, определяется суммой толщины центральной области и двух глубин проникновения оптической волны в двойные слои. Очевидно, что эф­фективная длина резонатора с зеркалами Брэгга значительно больше, чем у резонатора с металлическими зеркалами.

Отражательная способность зеркал Брэгга сильно зависит от по­лярного угла падения лучей и длины волны излучения. Аналитический результат можно получить только для падения лучей под прямым углом и только для длины волны Брэгга. Для других углов падения и произвольных длин волн коэффициент отражения рассчитывается при помощи численных методов. Рассмотрим зеркало Брэгга, отражающее излучение от изотропного источника света. В этом случае интен­сивность отраженного света определяется интегрированием интенсив­ности излучения, отражаемого во всех направлениях. Коэффициент отражения излучения определенной длины волны Л можно найти из соотношения

7г/2

• 27г • sin QdQ

7г/2

1

R (Л, 0) • 2тг • sin QdQ,

*■/2 2-7Г

J 2тт ■ sin QdQ о

(10.24)

а суммарную интенсивность отраженного зеркалом Брэгга излучения рассчитать так:

Г Ii{X)-R{)d, (10.25)

Jr-

где іі(А) — спектр интенсивности излучения активной области, попа­дающий на зеркало. Здесь предполагается, что для изотропных излу­чателей, к которым относятся активные области светодиодов, спектр излучения, достигшего зеркала Брэгга, не зависит от угла выхода лучей света из источника.

Эффективность зеркал Брэгга определяется интенсивностью от­раженного света. Необходимо также учитывать излучение, отражен­ное зеркалом от кристаллов светодиодов. Аналитически рассчитать оптимальную структуру светодиода со встроенным зеркалом Брэг­га, обладающего максимальным коэффициентом оптического вывода, невозможно. Для этого применяют специализированные компьютерные программы, позволяющие отслеживать траектории лучей внутри свето­диода.

Априори никогда не бывает ясно, будет ли данный светодиод с зер­калом Брэгга обладать более высоким коэффициентом оптического

вывода, чем без него. Использование зеркал со слоями различной толщины (меньшей или большей четверти длины волны) также может приводить к росту коэффициента оптического вывода светодиодов. Зер­кала Брэгга с переменной толщиной слоев обладают меньшей отра­жательной способностью, но более широкой полосой затухания по сравнению с четвертьволновыми зеркалами. Для светодиодов с широ­ким спектром излучения зеркала Брэгга с переменным периодом могут оказаться даже более предпочтительными.

Идеально, чтобы слои, входящие в состав зеркал Брэгга, были прозрачными для излучения рабочих длин волн, поскольку такие слои характеризуются незначительными потерями на поглощение. Однако использовать прозрачные слои удается не всегда, поэтому для изготов­ления зеркал Брэгга часто применяют поглощающие свет материалы. Максимальный коэффициент отражения поглощающих зеркал всегда меньше 100% , даже при бесконечном числе двойных слоев.

На рис. 10.8 показан пример частично поглощающего зеркала Брэг­га на основе Si/Si02. Кремний поглощает излучение с длиной волны А < 1,1 мкм, т. е. с hi/ > Ед. Однако видно, что на длине волны А « 1,0 мкм достигается высокий коэффициент отражения, хотя на этой длине волны кремний уже должен поглощать излучение. Объяс­нение этого заключается в большой разнице показателей преломления используемых материалов — кремния и ЭЮг.

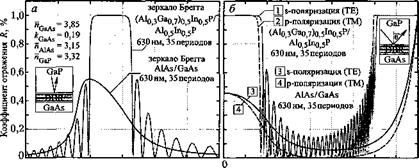
В светодиодах на основе AlInGaP/GaAs применяются как прозрач­ные, так и поглощающие зеркала Брэгга из материалов, согласованных по параметрам решеток с GaAs. Данная система материалов подхо­дит для изготовления высокоэффективных светодиодов видимой обла­сти спектра с А > 550 нм: зеленого, желтого, янтарного, оранжевого и красного свечения. В табл. 10.3 приведены характеристики некоторых прозрачных и поглощающих зеркал Брэгга, используемых в светоди­одах AlInGaP/GaAs (Kish, Fletcher, 1997). Видно, что поглощающие зеркала Alo. sIno. sP/GaAs имеют высокий коэффициент контраста, но их поглощающая природа ограничивает верхний предел максимальной отражающей способности. Зеркала Брэгга с высоким коэффициентом контраста обладают большей шириной полосы затухания. У прозрач­ных зеркал А1о,5ІПо,5Р/(АЮа)о,5Іпо,5Р незначительные оптические поте­ри, однако для получения светодиодов с высокими значениями коэффи­циента оптического вывода излучения такие зеркала должны состоять из большого количества двойных слоев. К тому же полоса затухания зеркал данного типа намного уже, чем зеркал с большой разницей показателей преломления.

На практике прозрачные слои размещаются на верхней части зер­кал Брэгга (ближе к эпитаксиальному слою) или вблизи нее, а по­глощающие слои —ближе к подложке. В промышленно выпускаемых светодиодах AlInGaP/GaAs каждая пара слоев зеркала Брэгга рассчи­тывается индивидуально с целью минимизации числа слоев и потерь на

поглощение, а также для расширения спектра отраженного излучения (Streubel, 2000).

В табл. 10.3 также приведены свойства зеркал AlAs/GaAs и SiC>2/Si. Нетрудно видеть, что система материалов Si02/Si обладает высоким коэффициентом контраста, однако в токопроводящих струк­турах она использоваться не может из-за диэлектрической природы S102. Зеркала AlAs/GaAs применяются в светодиодах с резонаторами, а также в поверхностно-излучающих лазерах с вертикальными резона­торами, работающих в диапазоне длин волн 880-980 нм.

Зеркала Брэгга с резонансом на длине волны максимума излучения не всегда являются оптимальными отражателями для светодиодов на поглощающих подложках. Хотя зеркала Брэгга при нормальных углах падения лучей имеют высокую отражательную способность, эта спо­собность резко снижается при углах падения, отличных от прямых. Поскольку пространственный угол (в интервале йв) при увеличении угла в растет по закону синуса, резонансную длину волны зеркала Брэгга для нормально падающих лучей на практике всегда желательно иметь больше длины волны максимума излучения.

На рис. 10.10 показаны зависимости коэффициентов отражения от длины волны и полярных углов падения лучей света, рассчитанные для прозрачных и поглощающих зеркал Брэгга. Видно, что зеркала Брэгга из прозрачных материалов обладают коэффициентом отражения, близ­ким к 100%, в то время как максимальный коэффициент отражения зеркал с поглощающими слоями GaAs равен всего 55%. Введение в зеркала Брэгга второго типа дополнительных пар слоев не приводит
к повышению их отражательной способности, поскольку предел 55% определен поглощающей природой слоев GaAs. Из рис. 10.10,6 от­четливо виден основной недостаток зеркал Брэгга — их отражательная способность высока только для лучей с малыми углами падения. При углах больше 20°, коэффициент отражения этих зеркал резко снижает­ся до значений, близких к нулю. Поэтому зеркала Брэгга почти совсем не отражают лучи с углами падения в в интервале 20°-70°. Этот недо­статок зеркал Брэгга является основной причиной потерь в светодиодах на основе AlInGaP, в которых активные слои выращиваются поверх отражающих слоев, расположенных на поглощающих подложках GaAs.

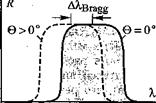
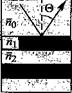
Теперь выведем формулу для нахождения критического угла ©с, при котором происходит резкое снижение отражающей способности зеркала Брэгга. На рис. 10.11, а показана структура зеркала Брэгга, а рис. 10.11,6 иллюстрирует понятие критического угла. Отметим, что здесь внешней средой является полупроводник с показателем прелом­ления Щ. Для нормальных углов падения (0 — 0°) условие Брэгга выполняется на длине волны, расположенной в центре полосы зату­хания с высоким коэффициентом отражения, называемой брэгговской длиной волны. На рис. 10.11, в показан сдвиг длины волны Брэгга при увеличении угла падения лучей. Следует отметить, что ширина полосы затухания зеркал не зависит от величины углов падения пока эти углы малы. Исходя из вышесказанного, можно записать следующее условие для критического угла Ос:

A^Bragg — Agragg(0 — 0 ) ABragg(0c) — — AAst0p band-

Используя выражение для длины волны Брэгга, зависящей от угла падения лучей, и выражение для ширины полосы затухания зеркала,

Рис. 10.11. Структура зеркала Брэгга, используемая в расчетах (а); зависи­мость коэффициента отражения от угла падения и определение критического угла (б); зависимость отражающей способности зеркала Брэгга от длины волны

для двух разных углов падения (в)

приведенное ранее в этой главе, можно вывести следующее соотноше­ние:

ABragg(0 = 0°) [l - cos (|0С)] = 2ABragg(0 = 0°) ~

Разделим обе части уравнения на ABragg(0 = 0°) и решим полученное уравнение относительно 0С:

(10.28)

Используя приближения: cos ж « 1 — (1/2)ж2 (справедливо для х, близ­ких к нулю) и arcosx и [2(1 — ж)]1'2 (справедливо для х, близких к единице), получим следующее выражение:

(10.29)

Из последнего уравнения видно, что величина критического уг­ла сильно зависит от показателя преломления внешней среды Щ (0С ос (поГ3/2). Отсюда следует, что для внешних сред с высоким показателем преломления характерны низкие значения критических углов. По этой причине при таких внешних средах зеркала Брэгга будут всегда иметь направленные характеристики отражения.

В качестве численного примера рассмотрим зеркало Брэгга AlAs/GaAs (пдіАв = 3,0, noaas = 3,5), роль внешней среды играет GaP (псаР = 3,1). Подставив эти значения в выражение (10.29), найдем величину критического угла 0Є = 20,5°, достаточно близкого к углам нормального падения. Даже такие высококонтрастные зеркала Брэгга, как зеркала на основе БіОг/Бі, в случае внешней среды - полупроводника с высоким показателем преломления не обладают всенаправленными отражательными характеристиками.

Для оптимизации зеркал Брэгга на практике были применены разные стратегии. В работе (Chiou et al., 2000) описан светоди­
од на основе AlInGaP с зеркалом Брэгга, состоящим из двух зер­кал разного типа, размещенных одно на другом. Одно из зеркал — А1о,5Іпо,5Р/(А1о,4Оао, б)о,5Іпо,5Р прозрачное с резонансом на длине вол­ны максимума излучения (590 нм), а второе дополнительное зерка­ло AlAs/GaAs расположено под первым и обладает большой разни­цей показателей преломления и поглощающей способностью (хотя и небольшой); его резонанс находится на длине волны на 10% больше соответствующей пику излучения, что дает возможность отражать лучи, падающие не под прямыми углами. Авторами работы было по­казано, что светодиоды с составными зеркалами Брэгга отличаются более высокими значениями коэффициента оптического вывода излу­чения.

В работе (Li et al., 1999) рассмотрены светодиоды с непериоди­ческими зеркалами, обладающими более широкой полосой затухания, а значит, и большими отражательной способностью и диапазоном допустимых углов падения лучей. Для расчета оптимальных непе­риодических зеркал Брэгга применяются методы численного модели­рования.

Из расчетов, приведенных ранее, следует, что увеличение разни­цы в показателях преломления слоев ведет к расширению диапазона углов, при которых зеркала Брэгга обладают высокой отражательной способностью. Использование таких высококонтрастных зеркал Брэгга, как AlGaAs/AlxOy, в структурах светодиодов было впервые предло­жено в работе (Chiou et al., 2003). Поскольку показатели прелом­ления AI2O3 и AlGaAs с большим содержанием алюминия примерно равны 1,75 и 3,25, коэффициент контраста таких слоев по показате­лю преломления составляет Ап = 1,5. Формирование слоев А1хОу, входящих в состав зеркал Брэгга, осуществляется в процессе окис­ления эпитаксиальных слоев AlAs, протекающего в среде водяных паров при 400-450 °С. Готовые слои АЦО^ непроводящие, поэтому для прохождения тока между подложкой и активными областями в слоях А1хОу необходимо оставлять участки AlAs, защищенные от окисления.

Зеркала Брэгга могут иметь большое электрическое сопротив­ление, мешающее протеканию тока через структуру излучающих устройств перпендикулярно ее слоям. Из-за этого сопротивления, особенно проявляющего себя в режимах сильного прямого смеще­ния, может нарушиться работа лазеров и светодиодов. Описаны (Jewell et al., 1989; Koyama et al., 1989) эксперименты с первы­ми поверхностно-излучающими лазерами с вертикальным резонатором (VCSEL), для которых было определено предельное напряжение пря­мого смещения ~ 30 В (Jewell, 1992), что предотвратило возможность лазерной генерации этих устройств в непрерывном режиме. Причиной возникновения больших сопротивлений в зеркалах Брэгга являются резкие гетеропереходы, создающие барьеры для перемещения носи­телей. К счастью, теперь научились полностью устранять барьеры в областях гетеропереходов методом параболического градиентного леги­рования соответствующих слоев (Schubert et al., 1992а, 1992b). Такая технология легирования широко применяется при изготовлении совре­менных зеркал Брэгга, поэтому проблем, связанных с их большим сопротивлением, сегодня больше не существует.