СОЕДИНЕНИЯ С НАТЯГОМ

ОСНОВЫ РАСЧЕТА ПРОЧНОСТИ СОЕДИНЕНИЙ

Несущую способность (прочность) цилиндрических и конических соединений с натягом в осевом и окружном направлениях ориентировочно оценивают по формулам

F = ndlp(f00 + tga), (1.1)

Мнр = ndHpf^/2, (1.2)

Где р — давление в соединении; fKP, foc — коэффициенты трения при кручении и осевом сдвиге; а — угол уклона конуса. Для цилиндрических соединений а=0.

Из этих зависимостей следует, что прочность зави­сит от эффективной площади сопряжения, контактного давления и коэффициента трения. Площадь сопряжения определяется геометрическими размерами соединения, которые назначают из условия обеспечения статической прочности и выносливости соединяемых деталей, предпо­лагаемого среднего значения коэффициента трения, а также по конструктивным соображениям. Для боль­шинства соединений с натягом, используемых в машино­строении, отношение l/d=0,5 ... 2. При выборе этого отношения необходимо учитывать, что соединения с короткими втулками допускают передачу больших нагрузок без локального проскальзывания при действии динамических крутящих моментов, однако хуже сопро­тивляются осевым и скручивающим нагрузкам при переменном изгибе вала.

У конических соединений необходимо обеспечивать условия их самоторможения, т. е. /ос>tga или 2/ос>/С, где К — конусность соединения. Из этого следует, что при /ос=0,1 конусность не может быть более 1:5. В табл. 1.1 помещены стандартные данные по номи­нальным значениям параметров конических поверхно­стей. При выборе конусности руководствуются возмож­ностями механической обработки, наличием измеритель­ных средств, способами демонтажа, конструктивными соображениями. При отсутствии производственных ограничений рекомендуется использовать конусности меньших значений, которые обеспечивают более высо­кую прочность соединений при осевых нагрузках, а в случаях, когда имеются несколько посадок на одном валу, малая конусность способствует снижению габа­ритов и массы узла.

Инженерные расчеты деталей соединения на проч­ность выполняют с использованием зависимостей Ляме. Среднее давление между соединяемыми элементами, изготовленными из различных материалов, определяют по формулам

_____________ 6_________

Р ' d (С1/Е1 + С2/£с) :

С _ 1 + (djdf с ^ 1 + (d/d2y

1 1 — (djdf Hi. 2 i _ (yd)2

Где 6 — натяг в соединении; Е, £2 — модули упругости материалов охватываемой и охватывающей деталей; Иь № — коэффициенты Пуассона.

При изготовлении втулки и вала из одного мате­риала

Р =—-—. (1-3)

<*(С1 + С2) * >

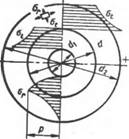
Рис. 1.2. Распределение напряжений (по Ляме) в деталях соединений

Контактное давление приводит - к возникновению нормальных радиальных ог и окружных а( напряженийв деталях (рис. 1.2).

В охватывающей детали наи­большие окружные напряжения

1 + (d/d2)2 растяжения at = р -—

1 — (d/a2)2

Возникают у внутренней поверхности. В охватываемой детали наибольшие окружные напряжения сжатия 2 (dJdf

А, = р——^ также находятся у внутренней по­

Верхности. Наибольшие радиальные сжимающие напря­жения Ог=—р находятся на контактирующих поверх­ностях охватывающей и охватываемой деталей.

Наиболее напряженным местом является внутренняя поверхность охватывающей детали, где, по теории наи­больших касательных напряжений, максимальные экви-

2 р

Валентные напряжения -------------------- " —

Аэкв = AT — °г = —

■ (d/d2)2

Для расчета деталей в упругой области предусмат­ривают

°э«в <0/. (1.4)

Из-за дискретности контакта фактические давления на отдельных участках сопрягаемых поверхностей могут быть значительно выше, чем определенные по фор­муле (1.3). В соответствии с этим пластические дефор­мации возникают. раньше, чем предусматривается рас­четом. Однако эти деформации проникают лишь на небольшую глубину детали. Условие (1.4) следует от­нести к распространению пластических деформаций на глубину, соизмеримую с величиной натяга. В том слу­чае, если при формировании соединения возможны заметные пластические деформации, следует учиты­вать, что несущая способность соединения может снижаться.

Считается [7], что в зависимости от величины натя­гов степень снижения прочности Л=26т—б/бт, где 6Т-— натяг, соответствующий моменту возникновения теку­
чести материала охватывающей детали; 6 — действи­тельный натяг. Пределы использования указанных за­висимостей ограничиваются значениями б=(1 ... 1,5)6Т.

Расчеты прочности соединений в упругопластической области рассматривают в специальной литературе [7]. —""При уточненных расчетах соединений на прочность необходимо учитывать, что на валу, вблизи торцов втулки, возникает концентрация давлений, если высту­пающие концы вала имеют достаточную длину [41]. Концентрация давлений может быть не только после формирования, но и при нагружении рала поперечными силами. В первом случае она осесимметрична, во вто­ром— больше со стороны сжатых волокон вала

Решения осесимметричных задач по определению • концентрации давлений указывают на заметную раз­ницу между максимальными величинами р, получае­мыми по способу Ляме и уточненным способам Напри­мер, расчетную величину давлений в месте их концент­рации при упругом контакте рекомендуют оценивать по формуле рк—р/х, где рк — концентрация контактных давлений, а х — безразмерный коэффициент, значения которого выбирают в зависимости от l/d по графику (рис. 1.3). Следует оговорить при этом, что решение осесимметричных задач выполнялось без учета нормаль­ной и касательной податливостей стыка [42], что при­водило к увеличению расчетных давлений. Задача опре­деления напряженного состояния посадки при наличии поперечных сил, действующих на вал при его изгибе, коренным образом изменяет картину напряженного состояния элементов соединения, переводя его в объем­ное и несимметричное. Необходимо учитывать, что при работе соединения с натягом в условиях переменного кручения и изгиба условия контактирования втулки с валом постепенно меняются из-за возможного мест­ного скольжения и износа торцовых частей втулки. Это приводит к новому распределению контактных дав­лений по длине сопряжения. Изменение исходных усло­вий контактирования может вызывать также релакса-

Рис. 1.3. Учет влияния выступаю­щих концов втулки

ЦИИ Напряжений. Учитывая изложенное, авторы ориентируются преимущественно на использование за­висимостей Ляме как наиболее простых и удобных для практики.