О контроле конусов в лабораторных условиях
В лабораторных условиях требуются измерения конусности, например для калибров, более высокой точности и раздельное определение отклонений формы конических поверхностей. Значительная часть существующих измерительных средств основана на прямом или косвенном измерении диаметров лишь в двух сечениях, в связи с чем на точности измерения углов конусов наряду с другими погрешностями сказываются отклонения формы. Погрешности формы можно определить по реальному профилю продольного сечения конуса. Для этого достаточно на различных расстояниях через равные промежутки длины замерить разницу радиусов по нижней Дн и верхней Дв образующим конуса относительно его исходного поперечного сечения, принимаемого у одного из оснований конуса. Затем по результатам измерений построить графические зависимости Дгн = <р (/„) и Аг„ = ф (/„), которые представляют собой отклонения радиусов реального профиля относительно геометрического, вычисляемые по формулам Дгн = Дн —/я{; Дгв = Дв—IJ, где /и —расстояние от исходного сечения конуса до измеряемого.
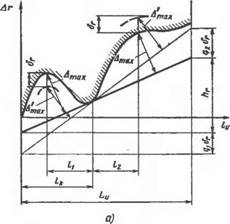
На рис. 6.12 показано разделение угловых отклонений и отклонений непрямолинейности образующей путем построения прилегающих прямых. Расстояния от реального профиля до прилегающей прямой выражают отклонения формы в продольном направлении Дл, а отклонения угла конуса в линейном выражении на длине LH определяют алгебраическим суммированием ординат прилегающих прямых h—hrB+hгв. Отклонения угла конуса в секундах, учитывая их малую величину
Д2а = 2 ■ 105ft/L„,
Предельная погрешность измерения на основе общих положений теории точности
62а= ± 2-105Л^------------------ р-—у^Л. (6.4)
LH Lg /
Где ДА — предельная погрешность измерения отклонения угла конуса в линейном выражении. Пренебрегая в выражении (6.4) вторым членом, получим
6га = ± 2-10»ДЛД*. (6.5)
Погрешность Aft складывается из погрешностей оценки отклонений нижней AftrH и верхней AhTB образующих конуса. Суммируя их геометрически как случайные и
Независимые величины, получим АЛ = Z~Ahrn + Ah,B. При АЛгВ = Ahm - Ahr имеем
Aft = 1,41 Aft,.. (6.6)
Отклонения AhT могут вызываться неточностями измерения разницы радиусов и отсчета отклонений hrH и Лгв по графикам. Предельные погрешности измерения перепада радиусов 6Г, в свою очередь, определяются погрешностями измерительного средства 6И и отсчета длин А/и. Как случайные и независимые, их также суммируют геометрически:
Бг = ]/2{би + А&[3]) . (6.7)
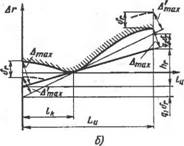
Погрешности AhT зависят еще и от положения прилегающей прямой относительно реального профиля. Если прилегающая прямая касается реального профиля в одной точке (рис. 6.13), то, согласно определению прилегающей прямой, на изменении ее угла наклона будут отражаться только отклонения 6Г в точках профиля, соответствующих ДтпЛ-, т. е. расстояниям от прилегающей прямой до наиболее удаленных точек профиля. В этом случае погрешности измерения конуса определяют из геометрических построений. Их суммарная величина
АЛ, = VM + M+ , (6.8)
Где б), -—точность отсчета ординаты hr прилегающей прямой по графику; q и <72 — коэффициенты, определяемые по формулам: 2 LK 2(L„-TK)
|
|
|
Рис. 6.13. Касание прилегающей прямой к одной точке профиля при его наибольших отклонениях: А— в произвольной точке на контролируемой длине конуса; б — в крайних точках контролируемой длины конуса |
В одной точке профиля: Ь2а — + 2,82-105-^— X
Х/2 (bl + Alli>){q + q) + bl.
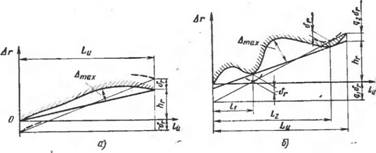
В случае касания прилегающих прямых реального профиля в двух крайних точках (рис. 6.14, а) погрешность измерения углов конусов АЛ, = ]/ 28? + бд, а с учетом выражений (6.5) — (6.7) погрешность измерения угловых отклонений конуса в секундах
Б2а = ± 2,82- 10в/4 (&l + Alli>) + 6l / La.
|
Рис. 6.14. Касание прилегающей прямой к реальному профилю: а — в двух крайних точках; б — в двух произвольных точках профиля |
Если прилегающая прямая касается реального профиля в двух произвольных точках на расстоянии U и
(рис. 6.14,6), между которыми находится максимальная величина отклонения реального профиля от прилегающей прямой, то из геометрических построений
Ahr = V${q3 + qd + bl, (6.9)
Где <?з и qt — коэффициенты, определяемые по формулам
На основе зависимостей (6.5) — (6.9) погрешность измерения углов конуса в секундах
= ± 2,82 /26L + AllPfa + QJ + Bl / LB.
Приведенный графо-аналитический способ определения угловых погрешностей путем суммирования ординат двух прилегающих прямых, построенных при неизменном положении конуса, исключает погрешности установки деталей при определении углов с помощью синусных линеек. Поэтому для оценки углов конусов в лабораторных условиях наряду с известными средствами измерения можно использовать устройства, обеспечивающие точный отсчет промежутков длины Д/ и перемещение измерительной головки вдоль неподвижного конуса или перемещение конуса относительно неподвижной измерительной головки.
Например, для этих целей нами использовалась станина большого инструментального микроскопа БМИ.