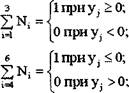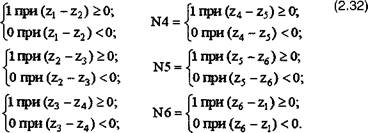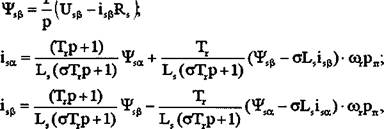ТАБЛИЦА ПЕРЕКЛЮЧЕНИЙ СИСТЕМЫ ПРЯМОГО УПРАВЛЕНИЯ МОМЕНТОМ
Таблица переключений в системе DTC, как было указано выше, является основным функциональным блоком, формирующим алгоритм управления системой в целом.
Количество строк в таблице определяется возможным числом сочетаний устойчивых состояний принятых релейных регуляторов с гисте- резисной характеристикой и с зоной нечувствительности. В простейшем случае, когда в качестве регуляторов потокосцепления статора и электромагнитного момента двигателя выбраны двухпозиционные релейные элементы, количество строк таблицы равно четырем. Состояния релейных регуляторов определяются их коммутационными функциями, которые, как было сказано ниже, обозначаются символами d'F и dM.
У двухпозиционных релейных регуляторов с гистерезисным допуском возможны три комбинации устойчивых состояний, то есть три вида реализуемых коммутационных функций, а именно, d = (1, 0); d = (1,-1) и d = (0,-1).
В первом случае квазиустойчивое значение регулируемой переменной Z будет находиться в диапазоне:
ZycT = [Z3afl н - (2зад+2ь)], (2.23)
где 2Ь - зона нечувствительности релейного регулятора (ширина гистерезисного допуска).
Во втором случае регулируемая переменная Z будет находиться в диапазоне:
Zycj = [(Zsafl - b) * (Z3afl+ b)]. (2-24)
В третьем случае этот диапазон составит:
ZycT = [(Zsafl - 2Ь) н - Z3afl]. (2-25)
Двухпозиционный регулятор первого вида наилучшим образом подходит для канала регулирования амплитуды вектора потокосцепления статора двигателя, так как задача регулирования этого канала сводится к стабилизации выходной переменной около заданного значения. В большинстве случаев регулятор этого вида используется в качестве регулятора потокосцепления статора двигателя.
Двухпозиционный регулятор второго вида может оказаться достаточным для канала регулирования электромагнитного момента двигателя, но не всегда. Поскольку в задачу регулирования этого канала одновременно входит отработка изменения управляющего воздействия с выхода линейного регулятора скорости и отработка изменения возмущающего воздействия (момента сопротивления со стороны механизма, приложенного к валу двигателя), как правило, в системах DTC приходится использовать релейный регулятор момента более сложной конфигурации.
Двухпозиционный регулятор третьего вида используется крайне редко, и поэтому здесь не рассматривается.
Внутреннее заполнение таблицы переключений, таким образом, представляет собой алгоритм работы преобразователя частоты. Для схемы с двумя двухпозиционными релейными регуляторами чаще всего используется следующий закон изменения результирующего вектора выходного напряжения преобразователя частоты:
- если оба регулятора находятся в верхнем положении, то есть заданные значения обеих контролируемых переменных превышают сигналы обратной связи, то результирующий вектор выходного напряжения в следующий момент времени необходимо переместить в следующий сектор на фазовой плоскости по направлению вращения вектора потокосцепления статора;
- если регулятор потокосцепления статора находится в верхнем положении, а регулятор электромагнитного момента - в нижнем положении, то есть сигнал обратной связи по электромагнитному моменту превышает задание, то результирующий вектор выходного напряжения в следующий момент времени необходимо переместить в предыдущий сектор на фазовой плоскости против направления вращения вектора потокосцепления статора;
- если регулятор потокосцепления статора находится в нижнем положении, а регулятор электромагнитного момента - в верхнем положении, то результирующий вектор выходного напряжения в следующий момент времени необходимо переместить через один сектор на фазовой плоскости по направлению вращения вектора потокосцепления статора (то есть, повернуть его в пространстве на 120 эл. град.);
- если оба релейных регулятора находятся в нижнем положении, то есть сигналы обратных связей по обеим контролируемых переменным превышают заданные значения, то результирующий вектор выходного напряжения в следующий момент времени необходимо переместить через один сектор на фазовой плоскости против направления вращения вектора потокосцепления статора (то есть, повернуть его в пространстве на минус 120 эл. град.).
Приведенный алгоритм может быть представлен табл. 2.1.
|
Таблица 2.1.
|
Номера результирующих векторов в этой и в последующих таблицах соответствуют нумерации, принятой в п.1.2 и приведенной на рис. 1.14.
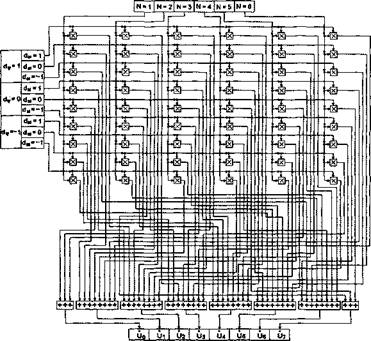
Реализация таблицы переключений при математическом моделировании системы DTC, может быть выполнена различными путями. Здесь принято целесообразным построение таблицы переключений с помощью типовых динамических блоков, так как это существенно упрощает операции стыковки отдельных элементов системы для объединения их в общую математическую модель. Структурная схема, реализующая первую таблицу переключений, приведена на рис.2.13.
Структурная схема построена с использованием блоков умножения переменных и сумматоров, реализующих операцию логического умножения (операцию “И”). Единичные сигналы, соответствующие номерам фазовых секторов (столбцы таблицы) поступают в схему с выхода определителя фазового сектора. Единичные сигналы, соответствующие состоянию релейных регуляторов (строки таблицы) поступают в схему с выхода формирователя строк таблицы переключений. В иных комментариях структурная схема рис.2.13 не нуждается.
В наиболее употребительном и чаще всего встречающемся в публикациях [28,30,38] варианте таблицы переключений используются двухпозиционный релейный регулятор потокосцепления и трехпозиционный релейный регулятор электромагнитного момента двигателя. В этом случае таблица переключений содержит шесть строк, причем строки, соответствующие среднему, нулевому состоянию релейного регулятора электромагнитного момента - пассивны. Под пассивным состоянием таблицы переключений здесь и далее понимается такая комбинация управляющих сигналов с выхода таблицы переключений, при которой результирующий вектор выходного напряжения преобразователя частоты принимает одно из двух нулевых значений. Нулевые значения результирующего вектора выходного напряжения преобразователя частоты U0 и U7 соответствуют закрытому состоянию силовых электронных ключей анодной или катодной группы, соответственно.
|
Состояние релейных регуляторов |
N =1 |
N = 2 |
N = 3 |
N = 4 |
N = 5 |
N =6 |
|
|
d* = 1 |
dM = 1 |
U2 |
u3 |
u4 |
u5 |
ufi |
U-| |
|
Q. II О |
U7 |
U0 |
u7 |
U0 |
u7 |
U0 |
|
|
dM = -1 |
U6 |
Ui |
u2 |
u3 |
U4 |
u5 |
|
|
о. II о |
dM = 1 |
U3 |
u4 |
U5 |
u6 |
Ui |
U2 |
|
dM = 0 |
U0 |
u7 |
U0 |
u7 |
U0 |
u7 |
|
|
dM = -1 |
u5 |
u6 |
Ui |
U2 |
u3 |
U4 |
Структурная схема, реализующая эту таблицу переключений, приведена на рис. 2.14.
<gl|N«2|N«3|N = 4|N»s|N = g~|
магнитного момента формирует тот или иной пространственный вектор выходного напряжения. Благодаря этому снижается частота пульсаций электромагнитного момента вокруг среднего значения и повышается устойчивость работы системы DTC. Однако, известны варианты построения таблицы переключений из шести строк, в которых одна или обе строки, соответствующие среднему (нулевому) состоянию релейного регулятора электромагнитного момента, активны. Например, в следующем варианте таблицы переключений активна строка, соответствующая коммутационным функциям d'F =1 и dM = 0. Переход релейного регулятора электромагнитного момента из единичного состояния в нулевое здесь сопровождается поворотом результирующего вектора выходного напряжения преобразователя частоты на пространственный угол минус 60 эл. град, против направления вращения поля статора. Если же релейной регулятор электромагнитного момента возвращается в нулевое состояние из положения dM = -1, то поворот результирующего вектора выходного напряжения преобразователя частоты происходит на пространственный угол 60 эл. град, по направлению вращения поля статора.
Строка таблицы переключений, соответствующая коммутационным функциям d*F =0 и dM = 0, по-прежнему, пассивна. В этом случае из шести строк таблицы переключений активны пять. Сама таблица выглядит следующим образом:
Таблица 2.3
|
N=1 |
N = 2 |
N = 3 |
N = 4 |
N = 5 |
N =6 |
||
|
dy = 1 |
dM = 1 |
Up |
u3 |
u4 |
Us |
Ufi |
Ui |
|
dM = 0 |
Ui |
u2 |
U3 |
U4 |
U5 |
U6 |
|
|
dM = -1 |
U6 |
Ui |
u2 |
Us |
u4 |
U5 |
|
|
dvF = 0 |
dM = 1 |
U3 |
u4 |
U5 |
u6 |
U! |
u2 |
|
dM = 0 |
U0 |
U7 |
U0 |
U7 |
U0 |
U7 |
|
|
dM = -1 |
U5 |
U6 |
U! |
u2 |
U3 |
u4 |
Структурная схема, реализующая эту таблицу переключений, приведена на рис. 2.15.
Возможен вариант построения таблицы переключений из шести строк, когда активны все строки. В этом случае конфигурация двухпозиционного релейного регулятора потокосцепления статора должна быть изменена. Коммутационная функция регулятора должна иметь вид d^ = (1,-1). Тогда строка таблицы переключений, соответствующая коммутационным функциям dT = -1 и dM = 0, активизируется следующим образом. Переход релейного регулятора электромагнитного момента из единичного состояния в нулевое сопровождается поворотом результирующего вектора выходного напряжения на пространственный угол 60 эл. град, по направления вращения поля статора, а возвращение регулятора в нулевое состояние из положения dM = -1 сопровождается поворотом результирующего вектора выходного напряжения на пространственный угол 60 эл. град, по направления вращения поля статора.
|
Наилучшие возможности управления обеспечиваются при использовании трехпозиционных релейных регуляторов как в канале регулирования потокосцепления статора, так и в канале регулирования электромагнитного момента двигателя. В этом случае таблица переключений содержит девять строк, причем пассивна только строка, соответствующая среднему, нулевому состоянию обоих релейных регуляторов. Остальные восемь строк таблицы переключений - активны, причем каждому столбцу, то есть каждому положению вектора потокосцепления статора на фазовой плоскости, при определенном сочетании состояний релейных регуляторов может соответствовать любое из шести возможных положений пространственного вектора выходного напряжения преобразователя частоты. |
N=1 |
N = 2 |
N = 3 |
N = 4 |
N = 5 |
N =6 |
|
|
dvF = 1 |
сім = [1] |
U2 |
u3 |
u4 |
U5 |
u6 |
Ui |
|
dM = 0 |
Ui |
u2 |
U3 |
U4 |
U5 |
u6 |
|
|
dM = -1 |
Ue |
Ui |
U2 |
u3 |
u4 |
U5 |
|
|
о. н о |
сім = 1 |
u2 |
U3 |
u4 |
U5 |
u6 |
Ui |
|
dM = 0 |
U0 |
U7 |
U0 |
u7 |
U0 |
u7 |
|
|
dM= -1 |
Ci |
u2 |
U3 |
u4 |
U5 |
U6 |
|
|
d4,= -1 |
dM = 1 |
u3 |
u4 |
Us |
u6 |
Ui |
U2 |
|
сім = 1 |
u4 |
Us |
ufi |
u1 |
U2 |
u3 |
|
|
dM = 0 |
U5 |
U6 |
Ui |
U2 |
u3 |
U4 |
|
Структурная схема, реализующая эту таблицу переключений, включающую в себя девять строк, приведена на рис. 2.16. |
|
Рис.2.16. Структурная схема, реализующая таблицу переключений, приведенную в табл. 2.4. |
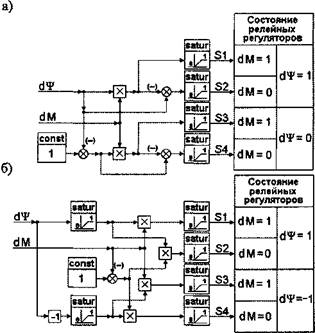
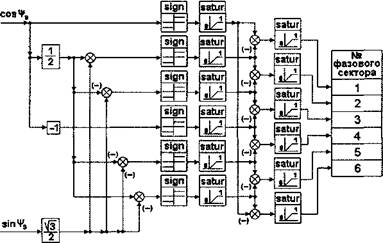
Формирователь строк таблицы переключений преобразует выходные сигналы релейных регуляторов потокосцепления статора и электромагнитного момента двигателя в переключательные функции, соответствующие номерам строк таблицы переключений. Таблица переключений силовых электронных ключей может содержать разное количество строк, причем состав таблицы выбирается предварительно, до начала построения системы. Следовательно, для каждого варианта таблицы переключений должен существовать свой формирователь строк. Или же может быть использован универсальный формирователь строк, построенный для таблицы переключений, содержащей 9 строк. Тогда для таблицы переключений, содержащей меньшее количество строк, ряд входов и выходов этой субсистемы просто не используется. Выбор того или иного варианта реализации этого блока принадлежит разработчику. Здесь рассмотрены оба варианта подхода к построению формирователя строк таблицы переключений в виде субсистемы.
В любом случае формирователь строк таблицы переключений — это набор схем совпадений, входами которых являются выходные сигналы релейных регуляторов потокосцепления статора и электромагнитного момента двигателя. С помощью элементарных динамических звеньев схема совпадений проще всего реализуется блоком умножения переменных. На один вход блоков умножения подается выходной сигнал трехпозиционного релейного регулятора электромагнитного момента двигателя. На второй вход подается преобразованный сигнал с выхода релейного регулятора потокосцепления статора. В случае использования трехпозиционного регулятора преобразование осуществляется в соответствии с выражениями:
|
|
Эти преобразования выполняются с помощью блоков инвертирования сигнала, ограничения сигнала верхним и нижним пределами (saturation), суммирования сигналов и единичного постоянного входного воздействия (const). Таким образом, осуществляется разделение выходных сигналов на три группы в зависимости от состояния релейного регулятора потокосцепления статора. Дальнейшее преобразование направлено на выделение сигналов, соответствующих состоянию релейного регулятора электромагнитного момента двигателя при неизменном состоянии
релейного регулятора потокосцепления статора двигателя (є|/ = const) в соответствии с выражениями:
|1 при СІМ =1; 10 при dM = 1; 10 при dM =1; (2.27)
Sj = • 0 при dM = 0; Sj+i = 1 при СІМ = 0; Sj+2 = 0 при dM = 0;
(О при dM = -1; (О при СІМ = -1; 11 при dM = -1.
Эти преобразования выполняются с помощью блоков инвертирования сигнала, ограничения сигнала верхним и нижним пределами “satur” (saturation), суммирования сигналов и выделения модуля входного сигнала - “abs”.
Формирователь строк таблицы переключений, выполненный в соответствии со структурной схемой рис. 2.17, может быть использован при
любом другом количестве строк таблицы переключений. Так, если количество строк таблицы переключений равно 6, то в субсистеме рис.2.17 остаются не использованы выходы S7, S8, S9, при выходном сигнале релейного регулятора потокосцепления статора dY s = (1,0), или выходы S4, S5, S6, при выходном сигнале релейного регулятора потокосцепления статора d^, s = (1 ,-1). В этом случае выходам субсистемы S7, S8, S9 должны быть присвоены номера S4, S5, S6 соответственно. Однако, с тем, чтобы избежать избыточности в вычислительных субсистемах и исключить возможные ошибки, вызванные этой избыточностью, формируемый банк субсистем целесообразно дополнить структурами формирователей строк для каждого варианта таблицы переключений отдельно.
Как было сказано, наибольшее распространение получила система DTC, в которой используется таблица переключений из шести строк. Здесь возможны два варианта реализации формирователя строк таблицы переключений в зависимости от выбранной переключательной функции релейного регулятора потокосцепления статора. При выходном сигнале этого регулятора d^ s = (1,0) получается просто усеченная структура формирователя оказанной на рис. 2.17 (рис. 2.18).
Если в релейном регуляторе потокосцепления статора реализована переключательная функция d¥ s = (1,-1), структурная схема формирователя строк таблицы переключений несколько видоизменяется. Отсутствие нулевого состояния у релейного регулятора потокосцепления статора позволяет исключить внутреннее единичное постоянное воздействие, а вместо него использовать блок инвертирования сигнала.
Если оба релейных регулятора двухпозиционные, то в зависимости от их переключательных функций, возможны четыре варианта структурной схемы формирователя строк таблицы переключений.
Вообще говоря, возможных сочетаний - девять, но, как было указано выше, релейные регуляторы с переключательной функцией вида dx = (0,-1) практически не используются. Поэтому интерес представляют только варианты, обозначенные в табл.2.5 символом (+). Если релейный регулятор электромагнитного момента двигателя не содержит нулевого положения, то структурная схема формирователя строк таблицы переключений в зависимости от вида переключательной функции регулятора потокосцепления статора изменяется незначительно,
Если релейный регулятор электромагнитного момента двигателя имеет нулевое положение, то структурные схемы формирователя строк таблицы переключений
в зависимости от вида переключательной функции регулятора потокосцепления статора существенно изменяются. В том случае, когда релейный регулятор потокосцепления статора также имеет нулевое положение, используется внутреннее единичное постоянное воздействие, которое совместно с блоками умножения обеспечивает формирование единичных сигналов при dM = 0. Структурная схема показана на рис.2.21- ,а. Если релейный регулятор потокосцепления статора не имеет нулевого положения, к этой схеме добавляются также блоки инвертирования сигнала с ограничением - рис. 2.21 ,б.
|
Рис. 2.21. Структурная схема формирователя строк таблицы переключений при использовании двухпозиционных релейных регуляторов в канале регулирования электромагнитного момента двигателя - с переключательной функцией dM = (1,0) и в канале регулирования потокосцепления статора - с переключательной функцией d¥ s = (1,0) - (а) и dT s = (1 ,-1) - (б). |
Здесь рассмотрены все возможные варианты структурных схем формирователя строк таблицы переключений.
Как при математическом моделировании, так и при проектировании конкретных систем DTC разработчик может выбрать тот алгоритм и структуру, которые в наибольшей степени обеспечивают заложенные технические требования. Выбор диктуется только требованием наибольшей простоты структуры формирователя строк. В то же время рассмотренными вариантами структур таблиц переключений и формирователей строк не исчерпываются все возможности систем DTC. Вполне возможны и другие алгоритмические решения.
ОПРЕДЕЛИТЕЛЬ ФАЗОВОГО СЕКТОРА
Математическое описание и структурные схемы определителя фазового сектора базируются на векторной диаграмме рис.1.15. Если предположить, что в первый момент времени to результирующий вектор напряжения ориентирован в пространстве по направлению оси а, то вектор потокосцепления статора сдвинут в пространстве относительно него на угол |/sнач < 90°. Следовательно, в момент времени to вектор потокосцепления статора W энач находится в секторе 2.
Для успешной работы системы DTC определитель фазового сектора должен с возможно большей точностью фиксировать момент перехода вектора потокосцепления статора из одного сектора в другой. Исходной информацией для этого являются предварительно вычисленные значения составляющих потокосцепления в неподвижной системе координат 'J'sa и ^s(3 , а также амплитудное значение вектора потокосцепления ^sm. Поскольку определение фазового сектора, по сути дела, представляет собой тригонометрическую задачу, возможны различные варианты ее решения. Один из вариантов решения, предложенный в [37], основан на следующих преобразованиях:
(2.28)
|
|
где Ni - номер фазового сектора - рис.1.15, причем і - целое число
(і = 1.. .6 ),
yj - функция знака от следующих трех выражений (j = 1 ...3 ). Таким образом, получается шесть единичных прямоугольных функций, объединяющих три фазовых сектора, следующих подряд, один за другим, а именно:
|
Zj = N1 + N2 + N3; z2 = N2 + N3 + N4; (2-30) |
|
|
z4 =N4 + N5 + N6; z5 =N5 + N6 + N1;
Дальнейшее преобразование сводится к выделению единичных прямоугольных импульсов, соответствующих каждому из шести фазовых векторов. Это достигается вычитанием с дальнейшим использованием ограничений по знаку функции:
(Zj - z2) = N1 - N4; (z2 - z3) = N2 - N5; (z3 - z4) = N3 - N6;l (2-31)
(z4 - z5) = N4 - N1; (z5 - z6) = N5 - N2; (z6-щ) = N6-N3; J
Если из этих выражений исключить отрицательную часть, то в итоге получится комбинация из шести прямоугольных импульсов с единичной амплитудой. Длительность каждого импульса соответствует времени нахождения вектора потокосцепления статора 4*s в соответствующем секторе. Окончательные выражения для отыскания длительности фазовых секторов имеют вид:
|
|
|
N2 = |
|
N1 = |
|
N3 = |
Следует отметить, что в переходных режимах работы асинхронного двигателя в кривых изменения составляющих потокосцепления статораFsa и Ysp присутствует постоянная составляющая, достаточно быстро затухающая по экспоненциальному закону. Тем не менее, когда в определителе фазового сектора используются функции знака переменных, указанное обстоятельство может приводить к сбоям в работе системы. Поэтому предпочтительным является использование в качестве входных сигналов определителя фазового сектора тригонометрических зависимостей угла поворота вектора потокосцепления Ys с единичной амплитудой, как это рекомендовано в [34]. Они находятся по выражениям (2.14). Вычисления cos|/s и sin|/s могут быть выполнены непосредственно в определителе фазового сектора, но целесообразнее выполнить их в вычислителе ненаблюдаемых координат электропривода, как это и было сделано выше. На основании изложенного исходные уравнения для построения определителя фазового сектора несколько изменятся и примут следующий вид:
(2.33)
|
Уз = “80(00* V,); |
|
|
В остальном все вычислительные операции останутся без изменений.
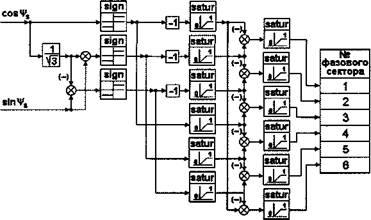
Для построения математической модели системы прямого управления моментом асинхронного электропривода определитель фазового сектора целесообразно представить в виде структурной схемы, приведенной на рис.2.22.
|
Рис. 2.22. Структурная схема определителя фазового сектора, вариант 1. |
Структурная схема реализована с помощью стандартных динамических и нединамических блоков. Блок, реализующий функцию знака (“сигнум”) на схеме обозначен “sign”.
Приведенное математическое описание и структурная схема не являются единственно возможным способом реализации определителя фазового сектора. Ниже приведены некоторые примеры решения той же задачи с использованием других вычислительных алгоритмов.
Частота изменения угла |/s принята равной 1 Гц, поскольку при дальнейших расчетах везде принята система относительных единиц. Дальнейшие преобразования сводятся к следующему. С помощью блоков ограничения функций верхним и нижним пределами создаются две последовательности импульсов. Одна из них позволяет разделить фазовую плоскость по оси а пополам
Вторая создает импульсы, включающие по два фазовых сектора, принадлежащих разным полуокружностям фазовой плоскости, и имеем вид:
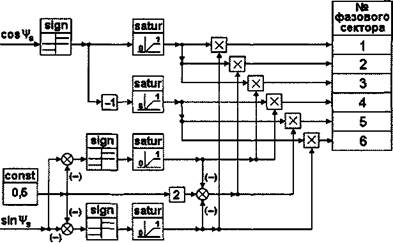
Структурная схема определителя фазового сектора, выполненного по этому алгоритму, приведена на рис.2.24.
|
Рис. 2.24. Структурная схема определителя фазового сектора, вариант 2. |
Эта структурная схема также реализована с помощью стандартных динамических и нединамических блоков, но в ней присутствуют блоки перемножения переменных. Блок, реализующий постоянное входное
воздействие с амплитудой 0,5, обозначен на схеме - const. Очевидно, что из-за наличия постоянного входного воздействия эта схема может работать только при единичных входных сигналах cos^ s и sin^ s.
|
(2.38) |
Построение определителя фазового сектора с помощью преобразования двухфазной ортогональной системы координат в симметричную трехфазную может быть выполнено на основании следующих исходных предпосылок. Прежде всего, исходные сигналы cos^ s и sin^ s превращаются (с помощью известного преобразования) в следующие сигналы [6]:
x2 = cosi|/s;
x3 = COS V|/g —— sin |/s = COS
Приведенные преобразования просты и в дополнительных ком-
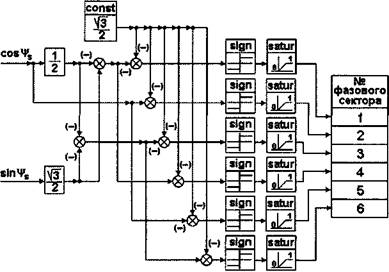
ментариях не нуждаются. Структурная схема определителя фазового сектора, выполненного по этому алгоритму, показана на рис.2.25.
|
Рис. 2.25. Структурная схема определителя фазового сектора, вариант 3. |
Эта структурная схема, как и предыдущая, содержит в своем составе постоянное входное воздействие с амплитудой 0,866, поэтому эта схема также может устойчиво работать только с единичными входными сигналами cos|/s и sin|/s. От этого недостатка свободен следующий вариант построения определителя фазового сектора с помощью косинуса тройного угла cos3|/s. Сначала с помощью входных сигналов cos|/s и sin|/s формируется функция cos3v|/ по известной формуле [6]:
|
(2.42) |
|
cos3 ш |
|
cos3w |
|
3sin2 |/s * cosj/s |
После этого определяются функции знака от входных и вычисленного сигналов:
хг = sigii(cos|/s); (2,43)
х2 = sign(cos3i|is); х3 = sigll(sim|/s).
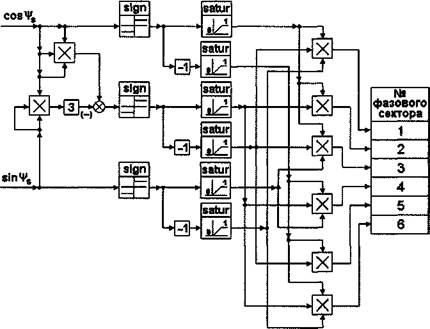
Структурная схема определителя фазового сектора, выполненного по последнему алгоритму, приведена на рис.2.26.
|
Рис. 2.26. Структурная схема определителя фазового сектора, вариант 4. Еще один вариант построения определителя фазового сектора может быть получен путем совмещения алгоритмов, заложенных в первый и в третий вариант вычислителя. Здесь с помощью известных преобразований определяются шесть тригонометрических функций со сдвигом на 60°, то есть на один фазовый сектор. Таким образом, получаются шесть опорных гармонических сигналов. Преобразование во многом подобно тому, которое использовано в третьем варианте построения определителя фазового сектора. |
Возможности построения определителя фазового сектора не исчерпываются приведенными примерами. В случае корректности тригонометрических преобразований любое другое решение даст положительный результат.
|
Рис. 2.27. Структурная схема определителя фазового сектора, вариант 5. Следует отметить, что независимо от выбора того или иного варианта вычислителей фазового сектора, все они при единичных гармонических сигналах на входе дают практически одинаковый результат. Выбор того или иного варианта реализации определителя фазового сектора следует производить применительно к каждой конкретной решаемой задаче. Поскольку в кривых изменения составляющих потокосцепления статора 'Fsa и могут присутствовать высшие гармонические составляющие, |
результаты расчета фазовых секторов на практике могут существенно расходиться в зависимости от выбранного алгоритма вычислений. Особенно сильное влияние на результаты расчета это оказывает при исследовании переходных процессов в системах DTC.
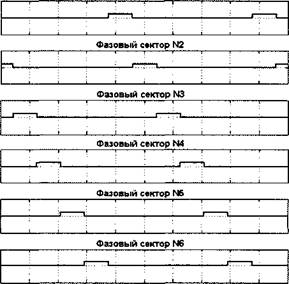
Результаты расчета фазовых секторов за два периода идеальных единичных входных гармонических сигналов, поданных с частотой 1 Гц, для всех рассмотренных вариантов построения определителя фазового сектора совпали с высокой степенью точности. Поэтому на рис.2.28 приведены общие для всех структур характеристики изменения во времени фазовых секторов.
|
Фазовый сектор N1
О 0,2 0.4 0.6 0.8 1 1.2 1,4 1,6 18 2 Время Рис. 2.28. Распределение фазовых секторов, в которых находится результирующий вектор потокосцепления статора, за два полных периода (два полных оборота вектора Ys) во времени. По оси ординат на рис. 2.28 отложены дискретные сигналы dTs, изменяющиеся в диапазоне (0...1) и фиксирующие (при значении dYs = 1) нахождение вектора потокосцепления статора 'Fs в соответствующем секторе фазовой плоскости. Как видно из результатов компьютерного расчета, графики функций Ni(t) представляют собой последовательность прямоугольных импульсов единичной амплитуды. Длительность импульсов составляет 60 эл. град. Импульсы следуют в строгой последовательности один за другим от первого фазового сектора N1k последнему N6. В начальный момент |
времени (при t = 0) вектор потокосцепления статора Ч^нач находится в фазовом секторе N2, что согласуется с принятым предположением, что в начальный момент времени вектор потокосцепления статора двигателя должен находиться именно в этом секторе. Переключение ступенчатых функций Ni происходит без временной паузы, а, следовательно, все рассмотренные варианты построения определителя фазового сектора отвечают условиям, оговоренным в начале этого подраздела.
ЯДРО ОТС
Таблица переключений системы прямого управления моментом в совокупности с определителем фазового сектора и формирователем строк образуют так называемое ядро DTC. В иностранной литературе эта часть системы называется «DTC core».
Функционирование ядра DTC не связано ни с номинальными данными, ни с параметрами электродвигателя, ни с параметрами источника электроэнергии. В нем не содержится также никаких блоков, имеющих настроечные параметры электропривода. В некоторых источниках [29, 35, 36] в состав ядра DTC включаются также релейные регуляторы потокосцепления статора и электромагнитного момента двигателя. Это, по - видимому, не вполне правомерно, так как ширина зоны нечувствительности релейного элемента и величина гистерезисного допуска являются важными настроечными параметрами системы электропривода. От правильного выбора ширины зоны нечувствительности и величины гистерезисного допуска в существенной мере зависит качество регулирования частоты вращения двигателя системой в целом. В связи с этим представляется целесообразным включить релейные регуляторы потокосцепления статора и электромагнитного момента двигателя в состав блока регулирования системы прямого управления моментом, с тем, чтобы все элементы, посредством которых осуществляется настройка конкретной системы электропривода, были бы сосредоточены в одном функциональном блоке.
Таким образом, ядро DTC представляет собой субсистему, в которой реализуется переключательная функция автономного инвертора в соответствии с принятым алгоритмом работы системы прямого управления моментом.
РЕЗУЛЬТАТЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ СИСТЕМ ПРЯМОГО УПРАВЛЕНИЯ МОМЕНТОМ
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ АСИНХРОННОГО ДВИГАТЕЛЯ ДЛЯ СИСТЕМ DTC
Приведенный в предыдущем разделе набор структурных схем типовых функциональных блоков систем прямого управления моментом, конечно, далеко не полный, но и он позволяет исследовать системы DTC различных конфигураций. Для того, чтобы замкнуть математическую модель, имеющийся банк структурных схем необходимо дополнить структурной схемой объекта регулирования. Здесь рассмотрены электроприводы на основе асинхронного двигателя с короткозамкнутым ротором. Однако, известны схемы DTC - управления на основе синхронных двигателей [36].
Математическая модель асинхронного двигателя базируется на известном математическом описании [22].
Однако при решении поставленной задачи нет необходимости использовать полную модель асинхронного двигателя. В системе DTC управление ведется только по статорным составляющим напряжения, тока и потокосцепления, а, следовательно, модель двигателя также целесообразно выполнить в статорных координатах. Для исключения из исходной системы уравнений (3.1) роторных переменных необходимо воспользоваться уравнениями связи составляющих токов и потокосце - плений двигателя. Как известно [22], эти переменные связаны между собой следующим образом:
Приведенная к статору система уравнений электромагнитного равновесия двигателя получается путем подстановки выражений (3.3) в систему уравнений (3.1): 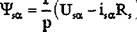
|
|
где - Тг электромагнитная постоянная времени роторной цепи двигателя.
Уравнения электромеханического равновесия двигателя включают в себя выражение электромагнитного момента (2.14) и основное уравнение движения электропривода [12]. Эта система уравнений имеют вид:
|
|
(3.5)
|
hp |
где Jz - суммарный приведенный к валу двигателя момент инерции ротора и механизма,
Мс - внешнее возмущающее воздействие (момент статического сопротивления со стороны механизма).
В соответствии с системами уравнений (3.4) и (3.5) построена структурная схема асинхронного двигателя в статорных координатах. Схема приведена на рис.3.1 и выглядит следующим образом: 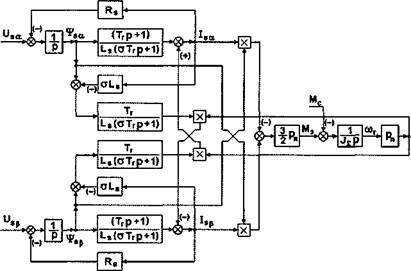
|
Рис.3.1. Структурная схема асинхронного двигателя в статорных координатах. |
Все переменные в этой структурной схеме относятся к статорной цепи двигателя. Для построения системы DTC используется информация о текущих значениях составляющих тока статора isa и і, а также может быть использован сигнал о частоте вращения ротора двигателя шг, если рассматривается система с прямой индикацией частоты вращения. В бездатчиковых системах этот сигнал не используется.