СИСТЕМА ДВУХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Вообразим грани прямого двугранного угла. Пусть ими будут, например, пол и одна из стен комнаты. Ещё лучше самому изготовить модель таких плоскостей из какого - нибудь подходящего материала: фанеры, картона или плотной бумаги.
На фиг. 18, а цифрой / обозначена знакомая уже нам горизонтальная плоскость. Любая перпендикулярная к ней плоскость называется, как мы знаем, вертикальной. Она
|
|
|
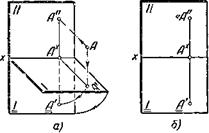
Отмечена на фигуре цифрой //. Линия их пересечения носит название оси проекций, или — короче — оси х (произносится: «икс»).
Представим себе, что внутри прямого угла, образованного горизонтальной и вертикальной плоскостями, имеется какая-либо точка А. Построим её прямоугольные проекции. Проведём через точку А два луча, перпендикулярных к первой и второй плоскости (такие лучи называются проектирующими). Основание А' первого перпендикуляра даст нам при этом горизонтальную проекцию заданной точки, основание второго — вертикальную. Чтобы отличить вертикальную проекцию от горизонтальной, воспользуемся той же буквой, но уже с двумя чёрточками справа: А" (читается: «а два штриха»),
.Можно сделать выполненные построения более наглядными, если воспользоваться нашей моделью плоскостей проекций. Примем данную точку А за центр небольшого деревянного шарика с двумя отверстиями по направлению любых двух его взаимно перпендикулярных диаметров.
Наденем шарик на два тонких прутка и расположим их так, чтобы они заняли положение проектирующих лучей. Прочертив карандашом или мелом прямые А'А* и А"А*9 параллельные пруткам, мы получим наглядное представление как о самой точке А, так и о её прямоугольных проекциях на первую и вторую плоскости (точки А А") и на ось х — точка Ах (фиг. 18, а). По двум точкам А/ и А", являющимся прямоугольными проекциями одной и той же точки Д мы можем уже найти её положение в пространстве. Точка А должна находиться одновременно на прямых А'А и А"А. Эти прямые на основании выполненных построений располагаются в одной плоскости. Их пересечение и будет искомой точкой А.