ПРОИЗВОДСТВЕННЫЙ ЧЕРТЁЖ

ПРЕДМЕТ И ЗАДАЧИ НАУКИ О ГРАФИЧЕСКИХ ИЗОБРАЖЕНИЯХ

Начертательная геометрия изучает геометрические свойства предметов. К этим свойствам относятся форма и взаимное расположение отдельных частей предмета, его величина, площадь поверхности и т. п. В отличие от гео­метрии, которой занимаются в школе, изучение простран­ственных форм производится графически — на материале соответствующего их изображения. Прежде всего выяс­ним, в чём состоит трудность такого изучения.

Во всяком пространственном предмете мы встречаем­ся, как известно, с тремя измерениями — длиной, шириной и высотой; плоскость же, на которой выполняются изо­бражения, двумерна, т. е. в ней различают только два из­мерения — длину и ширину. Естественно, что в этих усло­виях построение изображения пространственных предме­тов должно сопровождаться неизбежными искаже­ниями их формы: одному из трёх измерений не оказы­вается на плоскости места. Заметим, что при одних при­меняющихся способах изображений получаются боль­шие, при других меньшие искажения. Вовсе же избавить­ся от них мы не можем.

Наиболее просто строятся на плоскости изображе­ния треугольника, квадрата, круга и других плоских фигур.

Значительно труднее выполнить плоскостное изображе­ние какого-нибудь геометрического тела. Действительно, возьмём, например, куб. Все его грани представляют со­бой равные квадраты. Одну из этих граней мы можем изобразить на плоскости квадратом, смежные же две изобразятся с искажением своей формы. Фиг. 9, по­мещённая на стр. 22, поясняет сказанное на примере спи­чечной коробки.

Дать практически пригодные приёмы построения, ко­торые позволили бы выполнять плоскостные изображения пространственных предметов, и научить пользоваться этими приёмами — такова первая основная задача начер­тательной геометрии.

Вторая задача обратна предыдущей. Начертательная геометрия должна научить нас воссоздавать в нашем представлении пространственную форму и взаимное расположение отдельных её частей по выполненному изображению предмета.

Наконец, третья — метрическая — задача, связанная с различными измерениями, заключается в определении таких величин, как углы, длины, площади. Эти величины определяются в начертательной геометрии не путём вы­числений, а графически — посредством соответ­ствующих построений, выполняемых на основании имею­щегося изображения предмета.

Все рассмотренные задачи имеют очень большое зна­чение для практического черчения. От степени освоения этих задач зависит успех в работе. В самом деле, с пер­вой задачей мы встречаемся при выполнении изображе­ния предмета (задача проектирования), со второй — при чтении готового чертежа (производственная задача), с третьей же — метрической задачей — приходится иметь дело в том и другом случаях.

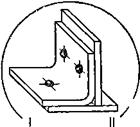
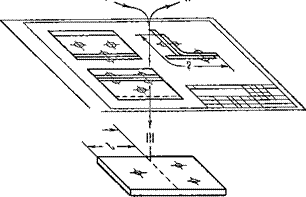
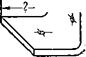
Поясним эти задачи примером. Рассмотрим деталь крепления фюзеляжа (корпуса) самолёта. Наглядное изображение детали обведено на фиг. 8 кружком. Имея деталь, мы должны уметь выполнить её чертёж, т. е. решить первую задачу начертательной геометрии. Чер­тёж детали помещён под наглядным её изображением. Эту задачу мы отметили на фиг. 8 цифрой I. Обратно, если будет дан чертёж детали, то надо научиться по нему воспроизводить её пространственную форму и тем самым решать вторую задачу (отмечена цифрой II). К третьей — метрической задаче, отмеченной на фиг. 8 цифрой III, в рассматриваемом примере относится определение по чер­тежу двух величин. Этими величинами являются длина (обозначена вопросительным знаком) той части про­филя, которая показана отдельно в левом нижнем углу фиг. 8, а в развёрнутом виде — под чертежом дета­ли, и расстояние I (читается: эль) линии сгиба от левого края профиля.

Так как начертательная геометрия даёт знания, кото­рые необходимы для успешного усвоения почти каждой специальности, то она имеет, кроме того, большое общеоб­разовательное значение. Начертательная геометрия разви­вает и обогащает наше пространственное представление.

«Необходимо развивать образное мышление, — гово­рила Н. К. Крупская, — оно связано с силой зрительного
восприятия, с умением наблюдать, с развитием зритель­ной памяти и образного воображения. Для квалифициро­ванного рабочего, для техника, инженера обладание всеми этими свойствами чрезвычайно важно. Оно влияет

На точность, чёткость работы, на развитие изобретатель­ства, на качество его».

Перейдём теперь к рассмотрению теории построения чертежей. Она позволит нам выявить то геометрическое основание, на котором производится это построение.

3 Производственный чертёж