Процессы и аппараты упаковочного производства

ПОДОБИЕ ГИДРОДИНАМИЧЕСКИХ ПРОЦЕССОВ

Запишем уравнение Навье-Стокса (3.56)-уравнение переноса количества движения - для вертикальной оси z:

Перемножим все элементы этого уравнения на соответствующие константы подобия:

Для сохранения тождественности полученного и исходного уравнений приравняем все коэффициенты, стоящие при одинаковых слагаемых:

(4.11)

(1) (2) (3) (4) (5)

Разделив в выражении (4.11) комплексы констант подобия (1), (3), (4) И (5) на (2), Получим соотношения между соответствующими силами и силами инерции:

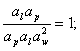
(4.12)

(1) (IV) (Ш) (IV)

Рассмотрим соотношение (IV) В выражении (4.12): Заменяя константы подобия на отношения соответствующих величин, получим:

или

Откуда

(4.13)

Т. е. уже известное безразмерное число - Критерий Рейнолъдса. Ом характеризует отношение сил инерции к силам трения и определи режим движения во всех сходственных точках подобных систем.

Соотношение (I) в уравнении (4.12) учитывает неустановившееся движение жидкости:

или

Откуда

(4.14)

Выражение (4.14) является критерием подобия, характеризующим неустановившееся состояние процесса, и называется Критерием гомохронности Но. Во всех сходственных точках подобных систем (натуры и модели) критерий гомохронности имеет одно и то же значение, если только в этих системах движение неустановившееся.

Из соотношения (//) получим критерий подобия, характеризующий отношение сил гидростатического давления к силам и инерции в подобных системах:

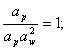или

Безразмерное отношение P/( W2) Называют Критерием Эйлера
При решении многих технических задач гидродинамики важно
определять не абсолютное давление Р В системе, а разность давлений Р Между какими-либо точками или сечениями потока жидкости. Поэтому обычно критерий Эйлера отражает влияние перепада гидростатического давления на движение жидкости и выражается следующим образом:

(4.15)

Наконец, соотношение (III) характеризует отношение силы тяжести к силе инерции:

или

Отсюда получаем новый безразмерный комплекс, называемый Критерием Фруда, Который отражает влияние сил тяжести на движение жидкости:

W2/(Gl) = Fr. (4.16)

Таким образом, решение уравнения Навье-Стокса, описывающее в общем виде процесс движения вязкой жидкости, может быть представлено критериальным уравнением вида

F (Но, Eu, Fr, Re) = 0, (4.17)

Которое называют Обобщенным (критериальным) уравнением гидро­динамики. Любая задача движения вязкой жидкости может быть решена путем нахождения зависимости между критериями, вхо­дящими в уравнение (4.17).

В уравнении (4.17) все критерии подобия, кроме Еu, являются определяющими, так как они составлены только из величин, выражающих условия однозначности. Поскольку при решении практических задач с помощью уравнения (4.17)обычно определяют величину Р, Входящую в Еu, то в этом случае уравнение (4.17)вписывают относительно определяемого критерия Еu:

Eu= F(Ho, Fr, Re). (4.18)

Например,

Eu=AHoqFrnRem, (4.19)

Где значения A, Q, N, M Обычно определяют опытным путем. В ряде случаев уравнение (4.18) дополняют геометрическим симплексом, отражающим влияние отношения длины канала к его диаметру – L/DЭ.

При установившемся движении критерий гомохронности может быть исключен из уравнения (4.17); тогда

(4.20)

F 2 (Eu, Fr, Re) = 0.

В том случае, если скорость движения жидкости трудноопределима (например, при естественной конвекции), вводят так называемые Производные, Или Модифицированные критерии подобия, Coставенные из основных критериев. В этих производных критериях трудноопределимая величина отражена с помощью других величин, которые сравнительно просто определяются аналитически или экспериментально.

Например, при естественной конвекции, возникающей вследствие разности плотностей, обусловленной различием температур в разных точках этой жидкости, трудно определить скорость движения конвективных токов. Критерий Фруда отражает действие силы тяжести, вследствие которых происходит перемещение частиц жидкости, но в него входит трудноопределимая величина W. Для того чтобы исключить величину W Из критерия Fr = W2/(Gl), Берут отношение двух критериев:

Re2/Fr = (w2l2p2/ )(gl3/w2) =L3p2g /

Полученный безразмерный комплекс величин является производным критерием и называется Критерием Галилея:

Ga = L3P2G / . (4.21)

Если умножить этот критерий на отношение ( 0 — )/ (где 0 и - плотности жидкости в разных точках), отражающее причину возникновения конвективных токов, получим новый производный критерий подобия -критерий Архимеда:

Аг = Ga( 0 — )/ =( L3 2G / )(( 0 — )/ ) (4.22)

В подобных системах, в которых процессы протекают при естественной конвекции под действием силы тяжести, необходимо соблюдение равенства критериев Ga или Аг.

Теперь получим критерии гидродинамического подобия Па основе аналитического метода (см. разд. 4.3).

Запишем уравнение Навье-Стокса (3.56) для оси z:

Для того чтобы привести это уравнение к безразмерному виду, проводят следующие преобразования.

Выразим WЯ = W (вместо WЯ Может быть записана скорость WН Или WЧ, В данном случае безразлично), т. е.

.

Тогда - безразмерная скорость. Аналогично z (x или y)= L; G(Z)= ; ;

В новых переменных уравнение (3.56) примет вид

(4.23)

Где I=1, 2, 3.

Разделив левую и правую части уравнения (4.23) на W2/L , получим

. (4.24)

Но

Тогда уравнение (4.24) примет вид

(4.25)

Cюда входят все уже известные критерии подобия гидродинамических процессов:Ho, Eu, Fr, Re.

Таким образом, двумя формально разными методами получено равное число одних и тех же обобщенных переменных-критериев подобия гидродинамических процессов, на основе которых составляют критериальные уравнения для решения тех или иных задач гидродинамики.

Это дает основание использовать достаточно формальный, но более простой способ подобного преобразования дифференциальных Уравнений, который заключается в следующем: критерии подобия находят, деля одну часть уравнения на другую и отбрасывая знаки математических операторов. Например, для уравнения Навье-Стокса (3.56) такое преобразование сведется к следующему:

Приняв за масштаб силу инерции и поделив на него все остальные, получим уже известные критерии подобия гидродинамических процессов: Но, Eu, Fr, Re. Аналогичным образом можно получить критерии подобия для процессов тепло - и массообмена, что и будет

Показано в соответствующих разделах.