Процессы и аппараты упаковочного производства

ДВИЖУЩАЯ СИЛА МАССООБМЕННЫХ ПРОЦЕССОВ

В соответствии со вторым законом термодинамики состояние замкнутой системы при взаимодействии двух фаз стремится к рав­новесию (см. гл. 2), что характеризуется равенством химических потенциалов компонентов фаз. Движущей силой переноса массы при этом является разность химических потенциалов того или иного компонента. Как отмечалось в гл. 2, поскольку химические потенциалы неидеальных систем определить достаточно сложно, то при анализе и расчете процессов массопереноса обычно рассмат­ривают изменение не химических потенциалов, а концентраций компонентов, определение которых значительно проще.

Обычно начальные и конечные рабочие концентрации заданы или определяются по уравнению материального баланса. Измене­ние рабочих концентраций по поверхности массообмена описы­вается уравнением рабочих линий. Эти линии используют для определения движущей силы процесса по всей поверхности F мас-сопередачи, а также для определения высоты Н массообменных аппаратов.

Процесс массопереноса протекает самопроизвольно при нали­чии разности между рабочими и равновесными концентрациями (при данных условиях температуры и давления), которые можно выразить через концентрации У и У * фазы Фу, а также Х и Х * для фазы Ф^.

Разность между рабочими и равновесными концентрациями и есть движущая сила массообменных процессов.

Движущую силу в концентрациях фазы Фу будем выражать так:

А^ = У — у* (при У > у*) или А^ == У* — у (при У < j.'*), а в кон­центрациях фазы Ф^ — Ах = Х — х* или Ах = х* — Х.

Таким образом, движущая сила характеризует степень откло­нения системы от равновесия. При установлении равновесия между фазами массообмен между ними прекращается.

Так же как и при теплообмене, величина движущей силы мас­сообменных процессов зависит от относительного направления движения фаз (противоток, прямоток и др.) Кроме того, на движущую силу большое влияние оказывает гидродинамическая структура потоков.

Рассмотрим вариант, когда в массообменном аппарате фазы движутся противоточно по отношению друг к другу, аппарат работает в стационарном режиме по модели МИВ (рис. 15-4, А). Полагаем, что перенос вещества происходит из фазы Ф^ в фазу Фу, т. е. У < у* . Для этого случая линия равновесия располагается выше линии рабочих концентраций (рис. 15-4,6).

Для каждой точки или сечения аппарата А^ == ^* — У, т. е. полу­чим aj^ , А^2 и т. д. Для этого же варианта движущую силу выразим в концентрациях фазы Ф^ (рис. 15-4, б). Тогда Лх=х—х*, т. е. Лх^ == Х^ — хТ, Лл-з и т. д.

Отсюда видно, что движущая сила изменяется с изменением

24

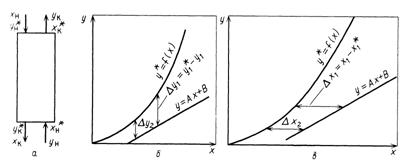
I • 15-4. К пояснению выражения движущей силы противоточного процесса ' ' < ^передачи:

Ма потоков в противоточном массообменном аппарате; Б, в-выражение движущей силы ' " "обменных процессов в концентрациях фаз соответственно Фу и Ф^

I > ючей концентрации. Поэтому для всего процесса (или для всей ' ксрхности F массопередачи) должна быть найдена средняя дви -

• щ11я сила. Для упрощения выводов полагаем, что аппарат рабо-!* 1 по противоточной схеме при идеальном вытеснении, линия I ншовесия прямая (т. е. У^ = wx), m>l и перенос вещества-из |i '>!»i Ф^ в фазу Фу (рис. 15-5).

Хпалогичная задача рассматривалась в гл. 11 при выводе дви -

• '.щей силы процессов теплопереноса. Поэтому по аналогии с

. юпереносом можно написать для массопереноса следующее | ражение движущей силы процесса А^р в концентрациях фазы /' (рис. 15-5,А):

« ея фазы Ф^ (рис. 15-5,6)-

г„ и Axg-большая, а А^^ и А. х^- меньшая разности концентраций на концах '^обменного аппарата.

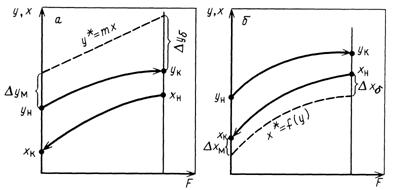
1. 15-5. К определению движущей силы процесса массопереноса в концентрациях. Ф,(а)иФ,(^)

При А^б/А^ < 2 движущая сила может определяться как сред­неарифметическая, т. е. А>'ср = (Д^ + А>^)/2.

Аналогичные выражения будут и для прямоточного движения фаз, участвующих в массообмене. Более общие зависимости для определения движущей силы, когда линия равновесия криволинейна и структура потоков отлична от идеального вытеснения, будут рассмотрены ниже (см. разд. 15.7.2).