Процессы и аппараты упаковочного производства

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРЕНОСА МАССЫ

Для вывода уравнений конвективного переноса массы восполь­зуемся основным уравнением переноса субстанций [уравнение (3.27)]:

Где (р - потенциал переноса массы; <у-плотность потока массы; у-источник переноса массы (принимаем, что у = 0, так как дополнительный подвод массы к потоку отсутствует).

В процессах массопередачи потенциалом переноса является кон­центрация, и поэтому 3(р/3т_^ Дс/дх.

Плотность потока массы Q складывается из двух составляющих:

В уравнении (15.24) величина Q^ = - D grade отражает плот­ность молекулярного переноса массы [первый закон Фика, уравне­ние (3.14)], а ^ = We- плотность конвективного потока массы.

Тогда основное уравнение переноса субстанции применительно к процессу переноса массы запишется следующим образом:

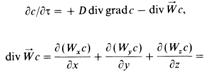
Поскольку при условии неразрывности потока величина

\'1дх} + (дУу/с1у) + (BWJQz} = 0, то уравнение (15.25) принимает

-I

В уравнении (15.25) значение div grade выражается как

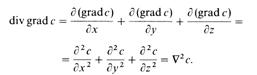
Таким образом, после проведенных преобразований уравнение I ^ 25) обращается в дифференциальное уравнение (3.46) конвек-и иной диффузии:

Юрое выражает в общем виде распределение концентрации • - мпонента в движущемся потоке при неустановившемся процессе 'ссопереноса.

При массопереносе в неподвижной среде И^ = W^ = W^ = 0, и ' лвпение (3.46) примет следующий вид:

Уравнение (15.29) называют Дифференциальным уравнением мо-кхлярной диффузии, или вторым законом Фика. Оно описывает (определение концентраций вещества в неподвижной среде моле-|ярной диффузией.

Отметим, что уравнение конвективной диффузии, поскольку ;ч>цесс переноса массы протекает в потоке, должно быть допол-ио уравнениями движения Навье-Стокса и неразрывности но­жа. Кроме того, перенос вещества приводит к изменению состава! и, следовательно, к изменению их физических свойств. Поэтому ктему дифференциальных уравнений, описывающих конвектив-мй массоперенос, следует дополнить также уравнениями, отра-нощими зависимость физических свойств фазы от ее состава. ючет такой системы уравнений представляет большие трудности, аналитическое решение этой системы уравнений оказывается тактически целесообразным только в тех случаях, когда возможны щественные ее упрощения. Поэтому часто для решения этой i лачи используют методы теории подобия.