ПРИНЦИПЫ ЛАЗЕРОВ

РЕЛАКСАЦИОННЫЕ КОЛЕБАНИЯ

Рассмотрим сначала случай, когда скорость накачки опи­сывается ступенчатой функцией. Таким образом, предполо­жим, что Щ = О при £ < 0 и #р(£) = Нр (не зависит от времени) при £ > 0. Предположим также, что лазер генерирует на од­ной моде, поскольку лишь при этом условии, строго говоря, справедливы скоростные уравнения. Как было видно в преды­дущей главе, скоростные уравнения являются нелинейными

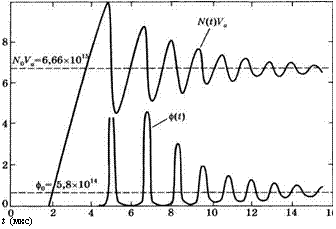
Рис. 8.1 Пример зависимости полной инверсии VaN(t) и числа фотонов ф(£) от времени в трехуровневом лазере (согласно работе [2])

Относительно переменных N(t) и ф(£), поскольку содержат произведение ф]У. Следовательно, найти аналитическое решение для подобных случаев оказы­вается невозможным, и приходится прибегать к численным методам [1,2].

В качестве характерного примера на рис. 8.1 приведены зависимости N(t) и ф(£), полученные путем численного расчета для трехуровневого лазера, та­кого как рубиновый лазер [2]. В этом случае при расчетах использовались следующие начальные условия для инверсии населенности iV(O) = ~Nt, где Nt — полная населенность, причем в момент времени t = О вся населенность сосредоточена на нижнем лазерном уровне (уровень 1, см. рис. 1.4а). Началь­ное условие для полного числа фотонов в резонаторе имеет вид: ф(0) = ф*, где ф* — некоторое небольшое число фотонов (например, фг- = 1), необходимое лишь для того, чтобы возникла генерация. Следует заметить, что зависи­мость, аналогичную показанной на рис. 8.1, будет также проявлять и четы­рехуровневый лазер, с той лишь разницей, что в последнем случае начальное условие будет иметь вид iV(O) = 0. Таким образом, если на рис. 8.1 начало временной оси совместить с точкой t = 2 мкс (где инверсия населенностей приблизительно равна нулю), то кривые на этом рисунке будут также пред­ставлять и четырехуровневый лазер. Можно теперь отметить некоторые осо­бенности кривых, представленных на рис. 8.1.

1. После момента времени t = 2 мкс инверсия населенностей будет непре­рывно возрастать вследствие процесса накачки. При этом число фотонов в резонаторе какое-то время остается небольшим (это начальное количество фотонов определяется квантовыми флуктуациями поля) до момента време­ни, когда кривая населенности пересечет пороговое значение (на рисунке N0Va = 6,66 • 1015). С этого момента (приблизительно при t > 4 мкс) число фо­тонов в резонаторе начнет возрастать. Действительно, из выражения (7.2.166) (для четырехуровневого лазера) или (7.2.246) (для квазитрехуровневого ла­зера) можно показать, что при N > Nc (где Nc — критическая или пороговая инверсия) имеет место d§/dt > 0.

2. После достижения порогового значения инверсии населенностей в те­чение некоторого времени число фотонов возрастает от начального значения
(ф* = 1) до значения, которое соответствует стационарному состоянию (на ри­сунке ф0 = 5,8 • 1014). При этом благодаря продолжающемуся процессу на­качки инверсия населенностей в течение этого времени может продолжать

Нарастать.

3. Когда число фотонов достигнет достаточно большого значения (при­близительно при ф > ф0), вынужденные процессы будут преобладать над про­цессом накачки и населенность начнет уменьшаться. В момент времени, ко­гда функция ф(£) достигает своего максимума, населенность ЛГ(£ ) спадет обрат­но до значения АГС. Из упомянутых выше выражений (7.2.166) или (7.2.246) можно показать, что при с? ф /сИ = 0 имеем N = ЛГС.

4. Вследствие все еще большой скорости вынужденного излучения (по­сле прохождения максимума функции числа фотонов) инверсия населенно­стей продолжит уменьшаться даже после значения Ыс. При этом лазер ока­жется в условиях ниже порогового, и число фотонов также продолжит умень­шаться.

5. Когда число фотонов уменьшится до значений ф < ф0, процесс накачки будет снова преобладать над процессами вынужденного излучения, и кривая инверсии населенностей будет вновь возрастать и, в конечном итоге, повтор­но пройдет все стадии, описанные пунктами 1-4.

В результате, функция числа фотонов ф(£) в резонаторе опишет регуляр­ную серию уменьшающихся по амплитуде импульсов, лазерных пичков, с равными интервалами времени между соседними пичками (около несколь­ких микросекунд). Выходное излучение (выходная мощность) будет вести себя аналогичным образом. Такой характер поведения генерации обычно называют затухающими (демпфированными)релаксационными колебания­ми. Поведение инверсии населенностей во времени N(1;) имеет схожий ха­рактер с опережением на полпериода осциллирующей функции ф(£) числа фотонов в резонаторе. Следует отметить, что поскольку, в конце концов, достигаются стационарные решения, определяемые выражениями (7.3.4а) и (7.3.46) для четырехуровневого лазера или (7.4.1) и (7.4.6) для квазитреху - ровневого лазера, численный расчет подтверждает, что эти решения соответ­ствуют устойчивому режиму работы.