ПРИНЦИПЫ ЛАЗЕРОВ

ПРОСТРАНСТВЕННО-ЗАВИСИМАЯ МОДЕЛЬ

Рассмотрим теперь случай, когда распределение моды и скорость накач­ки предполагаются пространственно зависимыми. Ограничимся обсуждени­ем только наиболее значимых результатов, предполагая, что активная среда накачивается вдоль всего объема пучком с поперечным гауссовым профи­лем. Для более детального рассмотрения данного случая, так же как и для случая однородной накачки, обратимся вновь к Приложению Д. Предполо­жим, что профиль напряженности поля снова описывается выражением (7.3.23), а пространственное распределение скорости накачки — выражени­ем (6.3.7), которое перепишем здесь для наглядности:

Поскольку здесь рассматриваются пороговые условия генерации, выра­жение (7.4.1) все еще записывается для среднего значения Ы9 т. е.

(Юс = (у/ое1)9 (7.4.12)

Где среднее значение определяется из выражения (7.3.20). Для получения пороговой скорости накачки следует помнить, что в каждой точке активной среды, ниже или в точке значения порога, выполняется условие баланса ме­жду числом атомов, возбуждаемых в процессе накачки, и числом атомов, которые спонтанно релаксируют. Таким образом, из уравнения (7.2.24а) по­лучаем Щ = [/ТУ£ + Щг, г)]/(1 + /)т. Усредняя данное выражение по распреде­лению интенсивности моды и используя выражение (7.4.12) для пороговой инверсии, получаем:

РдАУ + У

(<Зе +<*а)^т (7.4.13)

<Д>,

Если скорость накачки, представленную выражением (7.4.11), подста­вить в левую часть выражения (7.4.13) и рассчитать среднее значение Щ по профилю напряженности поля, мы получим выражение для пороговой мощ­ности накачки, полученное из выражения (6.3.25), которое перепишем здесь в слегка измененной форме (по аналогии с (7.4.4)):

Где величина В вновь определяется выражением (7.4.5).

После превышения накачки над порогом, используя условие (сіф/сИ) = 0, вновь находим, что среднее значение усиления должно равняться потерям; таким образом:

(М)0 = (М)с = у/ае1. (7.4.15)

Более детально расчет выходной мощности рассматривается в Приложении Д. По этой причине здесь приводятся лишь краткие выдержки и обсуждение
конечного результата. Сначала определяется коэффициент превышения на­качки над порогом через параметр х, как это описывалось в выражении (7.3.25), где минимальная пороговая мощность Рт#Л представляет собой по­роговое значение, достигаемое при ю0 <С юр и В <с 1 (т. е. когда оаА1г1 < у). Из выражения (7.4.14) получаем

Также определим нормированную выходную мощность, аналогично вы­ражению (7.3.27):

Лад

Р - І2 2

2(се +<уа)

После чего связь между параметрами х и у приводится к виду:

1+бМ1+у)

(7.4.18)

Где а = (ю0/юр)2. Следует отметить, что выражение (7.4.18) стремится к вы­ражению (7.3.33) при Б -> 0 (аа^/ < у), т. е. при пренебрежимо малом погло­щении на нижнем лазерном уровне. Если не принимать во внимание разницу в обозначениях, уравнение (7.4.18) имеет тот же вид, что и уравнение (25) в работе [16].

Теперь можно повторно рассчитать эффективность лазера в виде г|8 = = (йРоШ/йРр) = (Р8/Ртгь)(йу/йх). С помощью выражений (7.4.16) и (7.4.17) по­лучаем

Л 8=ЦР

(7.4.19)

Это выражение имеет тот же вид, что и для четырехуровневого лазе­ра. На рис. 7.116 приведена зависимость поперечной эффективности (или коэффициента заполнения активной среды по сечению), имеющей вид г), -(пюі / пю2)(йу / йх), для значений х = 10 и В = 1. Три графика, представ­ленные точками в виде треугольников, являются результатом машинных расчетов (см. работу [16]), тогда как пунктирная линия отображает резуль - тат интерполяции. Следует отметить, что когда (іи0/юр)2 1, значение т]*

Стремится к соответствующему значению для четырехуровневого лазера. В этом случае, действительно, населенность верхнего лазерного уровня, воз­никающая за счет поглощения основным состоянием, постоянно обновляет­ся за счет процессов вынужденного излучения, и, таким образом, поглоще­ние основным состоянием не приводит к снижению эффективности лазера. Однако для более высоких значений гі9 например, когда (ю^/и)р)2 = 1, погло­щение основным состоянием на краях профиля инверсии населенности при­водит скорее к спонтанному механизму, чем к вынужденному. Следователь' но, значение становится меньше, чем соответствующее значение для 46
тырехуровневого лазера. Однако можно показать, что дальнейшее увеличе­ние уровня накачки приводит к тому, что значения х и г|* будут стремиться к соответствующим значениям для четырехуровневого лазера. На самом деле, при очень больших значениях х нормированная выходная мощность у ста­новится достаточно большой, чтобы выполнялось условие В[Ш(1 + у)]/у 1. И в этом случае уравнение (7.4.18) становится идентичным уравнению (7.3.33).

Пример 7.5. Пороговые условия и выходная мощность в УЬ:УЖг лазере с продольной накачкой. В качестве типичного случая рассмотрим активную среду в виде диска из УЬ:УАО с толщиной 1 = 2,5 мм и процентным содержа­нием УЬ 6,5%, который продольно возбуждается излучением ГИ3+:А1203 ла­зера с длиной волны Хр = 941 нм [18]. Одна из поверхностей диска является плоской, и на нее нанесено отражающее покрытие с максимальным коэф­фициентом отражения для длины волны генерации (X = 1,03 мкм). Другая поверхность является вогнутой, радиус ее кривизны составляет 1 см; на эту поверхность нанесено покрытие с коэффициентом отражения по мощ­ности Я2 = 90% для длины волны генерации. Для приведенных условий вычисленное значение размера пятна в перетяжке пучка (т. е. на плоском зеркале) составляет ьи0 = 28 мкм; при этом размер пятна можно принять приблизительно постоянным по длине резонатора. Измеренный размер пятна накачки в лазерном диске составляет юр = 31 мкм. На рис. 7.14 при­веден график зависимости измеряемой выходной мощности от поглощае­мой мощности накачки; треугольниками обозначена зависимость, полу­ченная для температуры Т = 300 К.

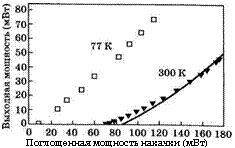Чтобы сравнить полученные результаты с теоретическими данными, необходимо отметить, что объемная концентрация атомов УЬ составляет « 9 • 1020 см-3; далее, измеряя значение коэффициента поглощения (для длины волны X = 1,03 мкм, см. рис. 6.86), получаем ста = 1,2 • 10~21 см2. Эф­фективное сечение перехода для вынужденного излучения вычисляется (со­гласно работе [18]) как ае = 18 -10~21 см2. Предполагая отсутствие прочих потерь, за исключением потерь, связанных с пропусканием выходного зер­кала (оптимальная связь на выходе), получаем у = у2/2 ~ (1 - #2)/2 = 5 • 10-2. Из выражения (7.4.14) получаем пороговую мощность Ргк = 83 мВт, кото­рую можно сравнить с экспериментальным значением 70 мВт (см. рис. 7.14). Теперь рассчитаем эффективность лазера при максимальном значении мощ­ности накачки 180 мВт. Имея у = у2/2 и принимая во внимание то, что данные

Рис. 7.14

Зависимость выходной мощности от поглощенной мощности накачки для Ті лазера на сапфире, возбуждаемого излучением лазера на УЬ-УАО при двух значениях температуры охлаждения — температуры жидкого азота (77 К) и комнатной температуры (300 К) (согласно работе [18])

На графике 7.14 выражены через поглощенную мощность накачки, необхо­димо в выражении (7.4.19) зафиксировать гр=1. Таким образом, выраже­ние для эффективности преобразуется к виду: г)8 = (1г/р)(и>$с1у/и)р(1х). Для вычисления коэффициента заполнения активной среды по сечению Цг ~(и)$(1у/и)‘р(1х) вначале из выражения (7.4.16) получаем Рт1Н = 6,5 мВт; далее, при Рр = 180 мВт имеем х = (Рр/Ршн) = 27,7. После чего эффектив­ность может быть оценена из рис. 4г из работы [18] в предположении, что г|, = йБ/йР, В = <заЫг1/у « 5, а = и)р/и)()« 1,1, (Р/¥гн) = ха2/( 1 + а2)( 1 + В)« 2,16, где значения величин 2? и, Р<Л определяются в упомянутой работе. Таким образом, получаем г|, = йБ/йР ~ 70% и г)8 = (Лу/&ур)т1* ж 63% .

Результат более точного расчета зависимости выходной мощности от мощности накачки, полученный непосредственно из выражения (7.4.18), представлен сплошной кривой на рис. 7.14. Из этих расчетов получаем более точное значение эффективности лазера г|8=59% для значения Рр = 180 мВт, которое можно сравнить со значением 56% , полученным из четырех точек на графике, соответствующих наибольшей эксперименталь­ной мощности.