ПЛОТНОСТЬ СОСТОЯНИЙ
Обратимся к рис. 3.24, где разрешенные состояния, определяемые соотношением (3.3.2), обозначены точками в плоскости (кх, ку) (ср. с рис. 2.2). Видно, что показаны только те состояния, которые относятся к уровню с п = 1. В самом деле, обычно Ь2 = 10 нм, тогда как Ьх и Ьу изменяются в диапазоне от 10 до 100 мкм, т. е. они в 103-104 раз больше, чем Ь2. Поэтому расстояния Ак2 между двумя соседними состояниями вдоль оси к2 (Ак2 — п/Ь2) примерно в 103-104 раз больше расстояний между ближайшими состояниями вдоль осей кх или ку. В данном случае разрешенные состояния расположены в широко разнесенных плоскостях, перпендикулярных оси к29 и поэтому удобно рассчитывать плотность состояний в каждой из этих плоскостей. Соответственно обозначим через АТ(к±) число состояний в каждой плоскости, например, в плоскости с п = 1 на рис. 3.24, поперечные вектора которых попадают в интервал между 0 и По аналогии с рассмотрением, относящимся к рис. 2.2, заметим, что число А1(к±) равно четверти площади круга радиуса к±, деленной на площадь АкхАку в /г-пространстве, приходящуюся на одно состояние,
|
М-А 2л -1 |
|
2£> _ Р к ~ ' |
|
П ' |
|
А^(1к_ В отличие от случая объемного полупроводника здесь величина р1° определяет число состояний на единичной площади, а не в единичном объеме. Поэтому далее будем использовать верхний индекс 2£>, чтобы отметить, что рассмотрение проводится в двумерном, а не трехмерном случае. Заметим также, что соотношение (3.3.6) справедливо как для валентной зоны, так и для зоны проводимости. Для того чтобы найти поверхностную плотность состояний в шкале энергий, запишем, например, для зоны проводимости, что р2Вс1Ес =р|в<1к±. Тогда из соотношения (3.3.6) получим: Р(3.3.7) Из (3.3.3) имеем, например, для подзоны с п = 1: К2=(2тс/П2)(Ес-Е1с). (3.3.8) Величина к1с1к1 в (3.3.7) легко определяется при дифференцировании обеих частей уравнения (3.3.8). Соотношение (3.3.7) при этом дает |
|
(3.3.6) |
|
(3.3.9) Видно, что плотность состояний р2в получилась не зависящей от к±9 т. е. от поперечной части энергии Ь2к /2тс (см. выражение (3.3.3)). Этот факт проиллюстрирован на рис. 3.25а, где показана зависимость величины р2В /Ь2 (фактически — объемной плотности состояний) от энергии электронов Ес (сплошная линия). Отсчет энергий ведется от дна зоны проводимости, и график отвечает диапазону энергий Е1с < Ес ^ Е2с, где Е2с — энергия в подзоне с п = 2. На самом деле, при Ес^ Е2с следует также учесть состояния, лежащие в плоскости кг = 2п/Ьг (не показаны на рис. 3.24). Плотность этих состояний, однако, такая же, как и в плоскости с п = 1, т. е. снова задается равенством (3.3.9). Таким образом, при Ес ^ Е2с полная плотность состояний будет равна сумме плотностей состояний в подзонах сп = 1ид1 = 2. Соответствующая зависимость показана на рис. 3.25а сплошной ступенчатой линией, обозначенной п= 1+2. Для сравнения, на рис. 3.25а пунктирной линией |
|
Р2В =тс/пН2. |
|
2(1/4)яй£ |
|
А _ |
|
Щк±) = |
|
А^г |
|
|
|
|
|
|
 |
|
 |
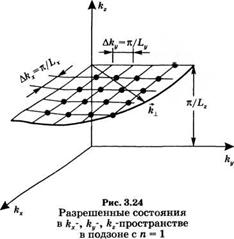
Рис. 3.25
А) Плотность состояний р*Р в зоне проводимости квантовой ямы, отнесенная к ширине ямы Ь2У в зависимости от энергии электронов Ес (сплошная ломаная линия). Здесь же показана плотность состояний рс в объемном полупроводнике того же состава (пунктирная линия).
Б) Зависимость энергии Ес от в подзонах проводимости сл=1ип=2
Показана плотность состояний рс в объемном полупроводнике того же состава, которая описывается соотношением (3.2.9а). Нетрудно показать, что кривая рс касается ступенчатой линии р2В /Ьг при Ес = Е1с, Ес = Е2с и т. д. Для полноты картины на рис. 3.256 изображена также зависимость Ес от (ср. с рис. 3.23). Таким образом, для любого значения энергии в диапазоне Еи ^ Ес ^ Е2с, рис. 3.25б непосредственно показывает соответствующую величину компоненты волнового вектора к электрона. Аналогичное рассмотрение может быть проведено также для плотности состояний в валентной зоне. Соответственно, плотность состояний р2В можно непосредственно получить из соотношения (3.3.9) заменой тс на ти для валентной зоны можно также построить зависимости, аналогичные приведенным на рис. 3.25. Поскольку в ОаАв ти = = 5тс, то на рисунке для валентной зоны, соответст
Вующем рис. 3.25а, размер ступенек по шкале плотности состояний р2В будет в 5 раз больше, а по шкале энергии Еи — в 5 раз меньше.