ЭЛЕКТРОННЫЕ СОСТОЯНИЯ
Для того чтобы рассчитать энергии электронов и дырок в квантовых потенциальных ямах, изображенных на рис. 3.216, необходимо знать, как разница ширин запрещенных зон AEg = Eg2 - Egl распределена между ямой в зоне проводимости АЕС и ямой в валентной зоне AEV. Решение этой задачи
(о так называемом смещении зон) затрагивает сложные аспекты физики полупроводников. Экспериментально для двух из наиболее важных типов КЯ найдено:
|
Ьчі 2 т,„ |
![]()
|
Ес’и ~ 2т, |
![]()
|
»а- |
![]()
|
0,67АЕё и АЕи = 0,33/Её в АЮаАз/ОаАэ/АЮаАз; 0,39ЛЕё и АЕ„ = 0,61АЕ^ в 1пР/1пОаА8Р/1пР. Для расчета энергий как электронов, так и дырок в соответствующих КЯ предположим, очень сильно упростив ситуацию, что ямы являются бесконечно глубокими (т. е. (АЕС, АЕи) —> оо). Потенциал ям будет при этом выглядеть как на рис. 3.22. Выберем ось г в направлении, перпендикулярном стенке ямы, поместив начало координат на одной из ее стенок. В соответствии с соотношением (3.2.1), волновые функции Блоха, как для зоны проводимости, так и для валентной зоны, могут быть представлены в виде: Ус, Дг) = и( 1±)е*х Г1 вЩпт/Ьг), (3.3.1) Где г± и к± — компоненты векторов г и к в плоскости вдоль ямы (в плоскости х, у), ап — положительное целое число. Отметим, что представленные в таком виде функции |/с у заведомо удовлетворяют граничным условиям = 0 при г = 0 и г = Ь2, т. е. на обеих стенках ямы. Если установить аналогичные периодические условия вдоль осей х и у, то получим: |

|
(1) АЕС ■■ (2) АЕс |
![]()
|
71 = 2 |
![]()
|
71 = 1 |
![]()
|
71= 1 |
Еик |
||
|
(М) |
____ ^ |
... іи | Е2и |
|
|
71 = 2 |
/ / ( |
||
|
(М) |
N ) / |
||
|
И. Ь. |
|
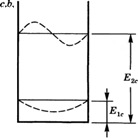
Рис. 3.22 Изображение уровней энергии состояний сп = 1ип = 2 (сплошные горизонтальные линии) и отвечающих им собственных функций (пунктирные линии) как в зоне проводимости, так и в валентной зоне при бесконечной глубине квантовой потенциальной ямы |
Кх = (1п/Ьх), (3.3.2а)
Ку = (тп/Ьх), (3.3.26)
Где I и т — также положительные целые числа. Отметим различие между соотношениями (3.3.2) и (3.2.4), которое, по существу, отражает факт использования в данном случае только положительных чисел. Разумеется, можно записать граничные условия так же, как в (3.2.5), т. е. допуская как положительные, так и отрицательные целые числа, и, тем не менее, получить аналогичные окончательные результаты. В приближении параболической зоны собственные значения энергий как в валентной зоне, так и в зоне проводимости определяются выражением:
П2П2п2
П2к2
2тС1}Ь2г
Где к‘(= ^ + Ц, а тс— эффективные массы электронов в зоне проводимости или дырок — в валентной зоне (для простоты рассматривается только масса тяжелых дырок); через Е1с и обозначены энергии первого состояния в КЯ (с п = 1) в валентной зоне или зоне проводимости, которые выра* жаются как
|
|
Следует отметить, что как в (3.3.3), так и в (3.3.4) энергия измеряется от дна зоны проводимости вверх — для электронов и от потолка валентной зоны вниз — для дырок. Отметим также, что при конечной глубине потенциальных ям электроны не полностью отражаются от их стенок, т. е. волновые функции не равны нулю на стенках, как это предполагается в выражении
(3.3.1) . Отличные от нуля волновые функции при этом существуют и в пограничном слое, а выражения для волновых функций и собственных значений энергии становятся более сложными [14]. Далее это обстоятельство рассматриваться не будет, поскольку оно приводит скорее к количественными, чем к качественным изменениям приводимых ниже результатов.
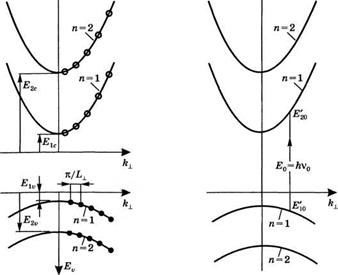
Приступая к обсуждению соотношений (3.3.3) и (3.3.4), рассмотрим вначале случай электронов с нулевым поперечным импульсом (к± = 0). Два нижних уровня энергии (с /I = 1 и м = 2) — как в зоне проводимости, так и в валентной зоне— показаны сплошными горизонтальными линиями на рис. 3.22, тогда как пунктиром показаны соответствующие собственные функции.
|
А Б
Рис. 3.23 Зависимость энергии Е от в подзонах с/г = 1и/г = 2 как в валентной зоне, так и в зоне проводимости в полупроводниковой КЯ: |
А) начало системы отсчета энергий для подзон проводимости находится у нижнего края зоны проводимости объемного полупроводника, и значения энергии увеличиваются вверх. Начало системы отсчета энергий для валентных подзон находится у верхнего края валентной зоны объемного полупроводника, и значения энергии увеличиваются вниз;
Б) шкала энергий является общей для всех подзон; начало системы отсчета энергий для подзон проводимости находится у верхнего края валентной зоны объемного полупроводника, и значения энергии увеличиваются вверх.
Согласно выражению (3.3.3) имеем: Е2с = 4Е1с, причем аналогичное соотношение справедливо также и для валентной зоны. Если теперь рассмотреть электроны с > 0, то зависимость энергии Е от к± для каждого из рассмотренных выше состояний с д = 1, п=2 ит. д. будет такой, как показано на рис. 3.23а. Видно, что теперь в зоне проводимости и в валентной зоне появляются отдельные подзоны. На этом же рисунке заполненными окружностями в валентной зоне и незаполненными окружностями в зоне проводимости показаны возможные состояния, полученные с помощью соотношения
(3.3.2) . Отметим, наконец, что при описании переходов между валентными подзонами и подзонами проводимости иногда удобнее использовать альтернативную систему отсчета энергий, которая начинается от потолка валентной зоны объемного полупроводника, увеличиваясь вверх, и обозначена как Е' на рис. 3.236. Переход между штрихованой Е' и нештрихованой Е системами отсчета энергий по-прежнему задается соотношениями (3.2.3), в которых Ес и Еи определяются выражением (3.3.3).
Пример 3.9. Расчет первых уровней энергии в квантовой яме СаАэ/ АЮаАв. Возьмем Ьг = 10 нм и предположим, что массы электронов и дырок (тяжелых дырок) в КЯ в ОаАв такие же, как в объемном полупроводнике, т. е. тс = 0,067т0 и ти = тнн = 0,46га0. Из соотношения (3.3.4) получим, что Е1с = 56,2 мэВ и ЕХи = 8 мэВ. Если ограничивающим слоем, с обеих сторон, является А10^Оа^ 8Аэ, то Её2 = 1,674 эВ. Так как ширина запрещенной зоны в ОаАв составляет Её1 = 1,424 эВ, то получаем, что АЕё = 250 мэВ и отсюда АЕС = 0,652^ = 162,5 мэВ и АЕ1) = 0,35АЕ^ = 87,5 мэВ. Поскольку величина АЕ1с получилась сравнимой с АЕс, то видно, что приближение бесконечно глубокой ямы не слишком подходит для данного случая. Действительные значения можно определить при учете туннелирования через барьер, и, например, из рис. 9.1 в [3] находим, что Е1с = 28 мэВ и ЕХи = 5 мэВ.