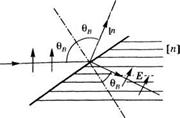
ОТРАЖЕНИЕ И ПРОПУСКАНИЕ ВОЛН НА ГРАНИЦЕ РАЗДЕЛА ДИЭЛЕКТРИКОВ
Рассмотрим волну, падающую на плоскую границу раздела двух диэлектрических сред с показателями преломления пх и п2 [2]. Если волна первоначально находится в среде с показателем преломления п1 и падает по нормали к поверхности раздела, то коэффициент отражения для напряженности электрического поля, или амплитудный коэффициент отражения, равен
Тогда как соответствующий коэффициент пропускания равен
T12 = 2n1/(nl + п2). (4.3.2)
Отметим, что если п1 < п2, то получаем г12 < 0; это означает, что напряженности отраженной и падающей волн сдвинуты по фазе на я. Конечно, если пх > п2, то г12 > 0, так что фазового сдвига при отражении не происходит. Можно также видеть, что, согласно соотношению (4.3.2), всегда t12 > 0, т. е. при пропускании фазового сдвига нет.
При падении, отличном от нормального, выражения для амплитудных коэффициентов отражения и пропускания становятся более сложными и зависят также от поляризации поля. Для волны с р-поляризацией (вектор Е лежит в плоскости падения) коэффициент отражения равен
Tan(0i -02)
|
(4.3.2а) |
![]() Ri2 = toьeTTtr
Ri2 = toьeTTtr
Тогда как для волны с в-поляризацией (вектор Е ортогонален плоскости падения) коэффициент отражения равен
|
(4.3.26) |
![]() Sin(0! ~02)
Sin(0! ~02)
Г12
|
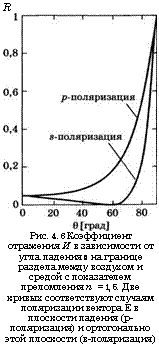
R Рис. 4.6 Коэффициент отражения И в зависимости от угла падения 0 на границе раздела между воздухом и средой с показателем преломления п = 1,5. Две кривых соответствуют случаям поляризации вектора Е в плоскости падения (р-поляризация) и ортогонально этой плоскости (в-поляризация) |
 8т(0х + 02) ’
8т(0х + 02) ’
Где 03 и 02 — соответственно углы падения и преломления. В качестве характерного примера на рис. 4.6 показаны графики зависимости энергетического коэффициента отражения, или отражательной способности, Я = (г12)2 от угла падения 0 для волны с р-поляризацией (вектор Е лежит в плоскости падения) и для волны с в-поляризаци - ей (вектор Е ортогонален плоскости падения) при пг = 1 и п2 = 1,52. При 0 = 0 оба коэффициента отражения очевидно равны и, согласно (4.3.1), составляют Я = [(п1 - п2)/(п1 + п2)]2 = 4,26%. Отметим также, что для р-поляризованной волны существует такой угол (0Б = 56,7° на рисунке), при котором Я = 0. В соответствии с (4.3.2а) это происходит при 0Х + 02 = п.
В этом случае ситуция может быть представлена с помощью рис. 4.7. Предположим, что угол падения 61 = 6В таков, что преломленный и отраженный лучи направлены ортогонально, т. е. 0Х + + 02 = я. При этом вектор Е в среде и соответствующий вектор поляризации будут параллельны направлению распространения отраженного луча. Поскольку отраженный луч можно рассматривать как порожденный вектором поляризации среды,
|
|
|
Отраженный Пучок |
|
Воздуху Оптическая среда |
|
Падающий пучок |
|
Преломленный Преломленный ПУЧ0К пучок |
|
Падающий Пучок |
![]()
|
Отраженный Пучок |
![]()
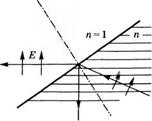
Рис. 4.7
Отраженный и преломленный пучки при падении под углом Брюстера:
(а) падение из оптически менее плотной среды и (б) падение из оптически более плотной среды.
В которой происходит преломление, то интенсивность этого отраженного луча равна в данном случае нулю, т. к. электрический диполь не излучает вдоль своей оси. Очевидный расчет, основанный на геометрической оптике, может теперь дать выражение для величины угла падения 0В, который называют углом Брюстера, или поляризующим углом. В соответствии с приведенным выше рассмотрением имеем:
|
Где &в |
![]() 0в+0в=л/2, (4.3.3)
0в+0в=л/2, (4.3.3)
Угол преломления. Согласно закону Снеллиуса имеем также
|
(4.3.4) |
![]() Явіиб^ =вт0Б.
Явіиб^ =вт0Б.
Поскольку, в соответствии с (4.3.3), справедливо соотношение =соб0в,
То из (4.3.4) получаем следующее выражение для угла Брюстера:
1ап0в = п. (4.3.5)
Отметим, что если направления распространения лучей заменить на противоположные (рис. 4.76), то интенсивность отраженного пучка, согласно (4.3.26), снова будет равна нулю, поскольку направления распространения преломленного и отраженного пучков опять ортогональны. Тогда, если в пучок, поляризованный в плоскости рисунка, установить под углом Брюстера плоскопараллельную пластинку из данного оптического материала, то на обеих поверхностях пластинки не будет никакого отражения. Предположим теперь, что плоскопараллельная пластинка с показателем преломления, например п = 1,52, установлена под углом Брюстера внутри оптического резонатора. В соответствии с рис. 4.6, коэффициент отражения з-поляризован - ного пучка на каждой из двух поверхностей раздела будет составлять Я = 15%. Таким образом, в-поляризованный пучок испытывает около 30% потерь за счет отражения на двух поверхностях. Если в лазере усиление за проход меньше 30%, то излучение с в-поляризацией не генерируется, так что лазерное излучение оказывается линейно поляризованным в плоскости падения на пластинку.